Задача о "многоруком бандите" (часть 1)
Задача является модельной для понимания конфликта между exploitation (применение, эксплуатация) и exploration (изучение, исследование).
Задача выглядит следующим образом. У нас есть автомат - “$N$-рукий бандит”, на каждом шаге мы выбираем за какую из $N$ рук автомата дернуть, т.е. множество действий будет $A=\{1, 2, …, N\}$. Выбор действия $a_t$, на шаге $t$, влечет награду $R^{(a_t)}$ при этом $R^{(a)}, a \in A$ есть случайная величина, распределение которой мы не знаем. Состояние среды у нас от шага к шагу не меняется, а значит множество $S=\{s\}$ тривиально, ни на что не влияет, так что мы его игнорируем.
Для простоты пока будем полагать, что каждому действию соответствует некоторое распределение, которое не меняется со временем Если бы мы знали, что за распределение, соответствуют каждому действию, то очевидная стратегия заключалась бы в том, чтобы подсчитать математическое ожидание для каждого из распределений, выбрать действие с максимальным математическим ожиданием и теперь совершать это действие на каждом шаге. Проблема ровно одна: про распределения мы ничего не знаем.
Однако, оценивать математическое ожидание некоторой случайной величины $\xi$ c неизвестным распределением мы умеем. Делаем $P$ экспериментов, получаем $\{\xi_p | p=1,…,P\}$ величин, берем среднее арифметическое:
\[\xi' = \frac 1 P \sum_{p=1}^P \xi_p ,\]это и будет оценка математического ожидания. Очевидно, что чем больше $P$ тем оценка точнее.
Объединяя всё вышеизложенное, получаем простую “жадную” стратегию.
Жадная (greedy) стратегия
-
Заведем массивы
- $\{P_a = 0 | a=1,…,N\}$, $P_a$ - сколько раз было выбрано действие $a$
- $\{Q_a =0 | a=1,…,N\}$, $Q_a$ - текущая оценка математического ожидания награды для действия $a$
-
На каждом шаге $t$.
-
Выбираем действие с максимальной оценкой математического ожидания:
\[a_t = argmax\{Q_a | a=1,...,N\}\] -
Выполняем действие $a_t$ и получаем награду $R_t$
-
Обновляем оценку математического ожидания для действия $a_t$ :
\[P_{a_t} = P_{a_t} + 1\] \[Q_{a_t} = Q_{a_t} + \frac 1 {P_{a_t}} (R_t - Q_{a_t})\]
-
Почему это не так хорошо как кажется?
Пример.
Пусть у нас есть “двурукий” бандит. Первая ручка всегда выдаёт награду равную 1, вторая всегда выдаёт 2. Действуя согласно жадной стратегии мы дёрнем в начале первую ручку (поскольку в начале у нас оценка математических ожиданий одинаковые и равны нулю) повысим её оценку до $Q_1 = 1$. И в дальнейшем всегда будем выбирать первую ручку, а значит на каждом шаге будем получать на 1 меньше, чем могли бы.
Т.е. желательно всё таки не фиксироваться на одной ручке. Понятно. что для нашего примера достаточно попробовать в начале каждую из ручек. Но если награда все-таки случайная величина, то единичной попытки будет явно не достаточно. В связи с этим предлагается следующая модификация жадной стратегии:
$\epsilon$-жадная ($\epsilon$-greedy) стратегия
-
Зададимся некоторым параметром $\epsilon \in (0, 1)$
-
Заведем массивы
- $\{P_a = 0 | a=1,…,N\}$, $P_a$ - сколько раз было выбрано действие $a$
- $\{Q_a =0 | a=1,…,N\}$, $Q_a$ - текущая оценка математического ожидания награды для действия $a$
-
На каждом шаге $t$.
-
Получаем значение $\alpha$ случайной величины равномерно расределенной на отрезке $(0,1)$
-
Если $\alpha \in (0, \epsilon)$, то выберем действие $a_t$ из набора $A$ случайно и равновероятно .
Иначе как и в жадной стратегии выбираем действие с максимальной оценкой математического ожидания:
\[a_t = argmax\{Q_a | a=1,...,N\}\] -
Выполняем действие $a_t$ и получаем награду $R_t$
-
Обновляем оценку математического ожидания для действия $a_t$ :
\[P_{a_t} = P_{a_t} + 1\] \[Q_{a_t} = Q_{a_t} + \frac 1 {P_{a_t}} (R_t - Q_{a_t})\]
-
Ясно, что если выбрать $\epsilon = 0$ мы вернемся к просто жадной стратегии. Однако, если $\epsilon > 0$, в отличии от просто “жадной”, у нас на каждом шаге с вероятностью $\epsilon$ присходит “исследование”.
Эксперимент
В книге Sutton and Barto предлагается следующий эксперимент.
Рассмотрим 10-рукий бандит. Выберем 10 чисел сообразуясь с нормальным распределением с центром в нуле и единичной дисперсией: $E = \{E_a | a=1,…,10\}$. Каждой ручке поставим соответствие нормальное распределение с математическим ожиданием из $E$ и дисперсией $1$ это будут 10 случайных величин, которые определяют награду за то, что мы дергаем соответствующую ручку.
Каждый эксперимент будет состоять из 1000 шагов. При этом мы заранее сформируем данные (т.е. для каждого шага запомним награду за каждую ручку), чтобы можно было повторять эксперименты меняя стратегию. Проведем набор из 2000 эксперементов. Для каждого шага будем считать среднюю награду по всем 2000 эксперементов.
Допустим в качестве средних для наград выбрали следующие величины (сгенерированы случайно, как и писалось выше из нормального распределения с математическим ожиданием нуль и единичной дисперсией):
| Ручка | Ср. награда |
|---|---|
| 1 | 0.089668 |
| 2 | -0.757752 |
| 3 | 0.497168 |
| 4 | 0.811979 |
| 5 | -0.367975 |
| 6 | -0.666402 |
| 7 | 0.432601 |
| 8 | 2.769230 |
| 9 | 0.943522 |
| 10 | -0.151123 |
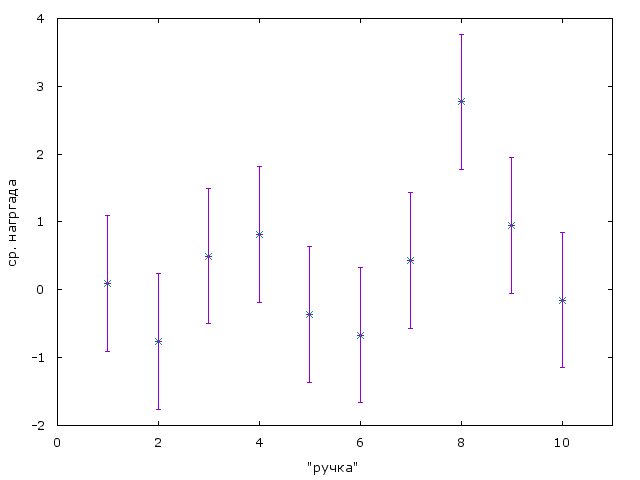
Посмотрим, что получается при таких условиях для стратегий с различными $\epsilon$:
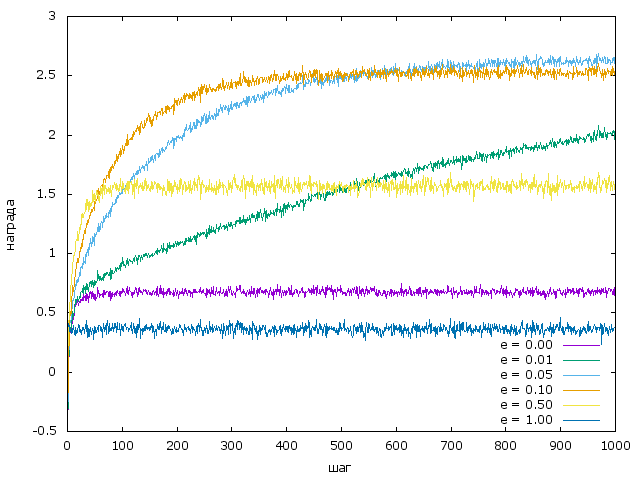
-
Худший результат выдает стратегия с $\epsilon = 1$, т.е. стратегия при которой на каждом шаге ручка выбирается случайно и равновероятно.
-
Просто “жадная” стратегия ($\epsilon = 0$) выдает, ожидаемо, несколько лучший резальтат, и находится на предпоследнем месте.
-
Стратегия с $\epsilon = 0.5$ сильно лучше двух предыдущих, однако, тратить половину ходов, выбирая ручку случайно, явно не приводит к успеху: начиная с некоторого момента полученная награда стабилизируется и явно не в максимальном значении.
-
Стратегия с $\epsilon = 0.01$ растет слишком медленно на начальном этапе (слишком мало исследований) и вероятнее всего догонит варианты с $\epsilon = 0.05$ и $\epsilon = 0.1$, но для этого ей надо больше времени
-
Оставшиеся две стратегии работают вполне не плохо. Правда достигнуть среднего $2.76923$ (т.е. собственно того, которое будет если дергать только 8-ю ручку) ни та, ни другая не смогли.
Код можно найти здесь.