Batch Normalization - одна из тех методик (или даже Tips&Tricks), которая существенно упростила тренировку, а следовательно и использование нейронных сетей в различных задачах. Понятно, что взлет ракетой нейронных сетей, за последние 5+ лет, обязан в основном серьёзному увеличению возможностей железок. Но удалось бы добиться такого рапространия нейронных сетей, и особенно глубоких нейронных сетей без batch normalization?

Главные наблюдаемые достоинства batch normalization это ускорение тренировки (в смысле уменьшения количества итераций для получения нужного качества) и некая допускаемая вольность в подборе параметров: и инициализации весов сети, и learning rate и других метапараметров обучения. Таким образом ценность batch Normalization для нейронных сетей сложно преувеличить, а значит есть смысл разобраться: что это такое и откуда проистекает польза при применении.

И вот тут начинается самое интересное. Ответ на первый вопрос “что это такое?” в целом не вызывает особой сложности (если подойти к делу формально и определить какие же преобразования добавляются в сетку), а вот про “откуда проистекает польза?” идут жаркие споры. Объяснение авторов методики подвергается серьёзной критике.

Мне понравилось как это сформулировано в [3]:

“The practical success of BatchNorm is indisputable. By now, it is used by default in most deep learning models, both in research (more than 6,000 citations) and real-world settings. Somewhat shockingly, however, despite its prominence, we still have a poor understanding of what the effectiveness of BatchNorm is stemming from. In fact, there are now a number of works that provide alternatives to BatchNorm, but none of them seem to bring us any closer to understanding this issue.”

Правда, стоит отметить, что у нас всё глубокое обучение и нейронные сети во многом можно описать теми же словами. Оно вроде работает и мы даже, в принципе, понимаем какие рычаги жать, чтобы ехало в примерно нужном направлении, но многие моменты так до конца и не объясняются.

Заканчивая лирику переходим к конкретике. Начнем разбираться с самого начала, а именно классической статьи [1] где методика BN и была впервые описана.

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

Авторы уже в заголовке статьи [1] анонсируют, что ускорение тренировки связано с тем, что применение BN позволяет уменьшить internal covariate shift. Следовательно, есть смысл разобраться, что такое covariate shift (отложив пока в сторону, что значит internal), а для этого надо обратиться к статье [2] на которую ссылаются авторы [1].

Covariate shift

Допустим у нас есть наблюдаемая величина $x$, и есть, зависящая от $x$, величина $y$. Мы хотим выяснить эту зависимость и научиться по $x$ находить $y$. Зависимость у нас вероятностная, т.е. есть некая условная вероятность, которая определяется при помощи плотности $q(y|x)$. А мы собственно и хотим восстановить эту плотность в виде функции $p(y|x, \theta)$, где $\theta$ это параметры, которые следует подобрать.

Чтобы решить задачу нам выдано некоторое количество пар $\{(x_n, y_n) | n=1,…,N\}$ в качестве тренировочного набора. Чтобы сформировать этот набор $x_n$ выбирались случайным образом из распределения с плотностью вероятности $q_0(x)$, а $y_n$ из распределения с плотностью вероятности $q(y | x_n)$. Каким-то образом “натренировав” наши параметры $\theta$ по этому тренировочному набору (не важно каким образом, например, использовав метод максимального правдоподобия). Мы решаем проверить, что же у нас получилось, а для этого нам выдают второй (проверочный) набор пар $\{(x’_m, y’_m) | m = 1,…,M\}$, который формируется аналогично первому, вот только $x’_m$ выбираются из распределения с плотностью $q_1(x)$. Ситуацию, когда $q_0(x) \neq q_1(x)$ в работе [2] называют covariate shift в распределении. При определенных обстоятельствах, такого рода изменение может дать существенную ошибку на проверочных данных у модели, которая вообще говоря очень хорошо работала на тренировочных.

Рассмотрим следующий пример (который взят из той же [2]).

Пример

Пусть $x \in \mathbb{R}$ и $y \in \mathbb{R}$, при этом зависимость $y$ от $x$ задаётся формулой:

\[y = -x + x^3 + \epsilon\]

$\epsilon$ - случайная величина, нормально распределенная с математическим ожиданием $\mu_{\epsilon} = 0$ и среднеквадратичным отклонением $\sigma_{\epsilon} = 0.3$.

Для тренировки мы наберем $N = 100$ пар, при этом $x$ будем выбирать нормально распределенным с $\mu_0 = 0.5$ и $\sigma_0 = 0.5$.

Зависимость $y$ от $x$ будем искать в виде линейной функции:

\[y = kx + c\]

Коэффициенты определим методом наименьших квадратов (МНК), т.е. решив задачу оптимизации:

\[\sum_{i=1}^{N} (y_i - (kx_i + c))^2 \to min\]

Как решать - понятно. Берём две производные (по $k$ и по $c$) приравняем их к нулю и получим (все суммирования по $i = 1,…,N$):

\[k = \frac {\sum x_i y_i - \frac 1 N \sum x_i \sum y_i} {\sum x_i^2 - \frac 1 N (\sum x_i)^2}\] \[c = \frac 1 N \sum y_i - k \frac 1 N \sum x_i\]

Визуализируем:

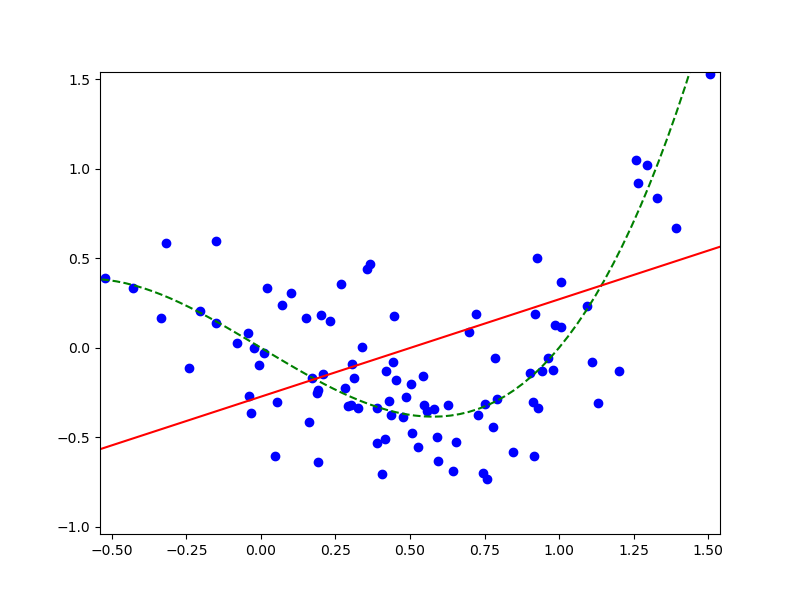
Здесь синие круги - это пары $(x_n, y_n)$, зеленый пунктир - “базовая” кривая $y = -x + x^3$, красная линия - наше линейное приближение модели.

А теперь выберем проверочный набор. При этом, чтобы продемонстрировать covariate shift, $x$ будем выбирать нормально распределенным, но с $\mu_1 = 0$ и $\sigma_1 = 0.3$. Впишем линейную зависимость по проверочному набору, используя МНК (желтая линия на рисунке):

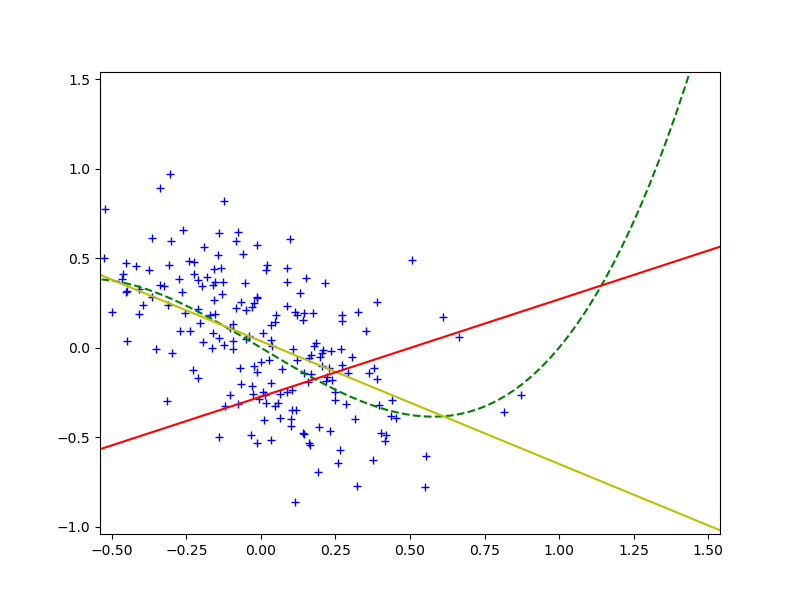
Очевидно, раз красная и желтая линии существенно не совпадают, то модель “наученная” по тренировочному набору для проверочного набора даёт плохой результат. В [2] предлагается, для того, чтобы погасить влияние covariate shift вместо МНК использовать взвешенный МНК, и оптимизировать функцию:

\[\sum_{i=1}^{N} \frac {q_1(x_i)} {q_0(x_i)} (y_i - (kx_i + c))^2 \to min\]

учитывая изменение распределения переменной $x$. Если воспользоваться этой методикой, то в качестве модели, обученной на тренировочных данных, получим фиолетовую линию на графике:

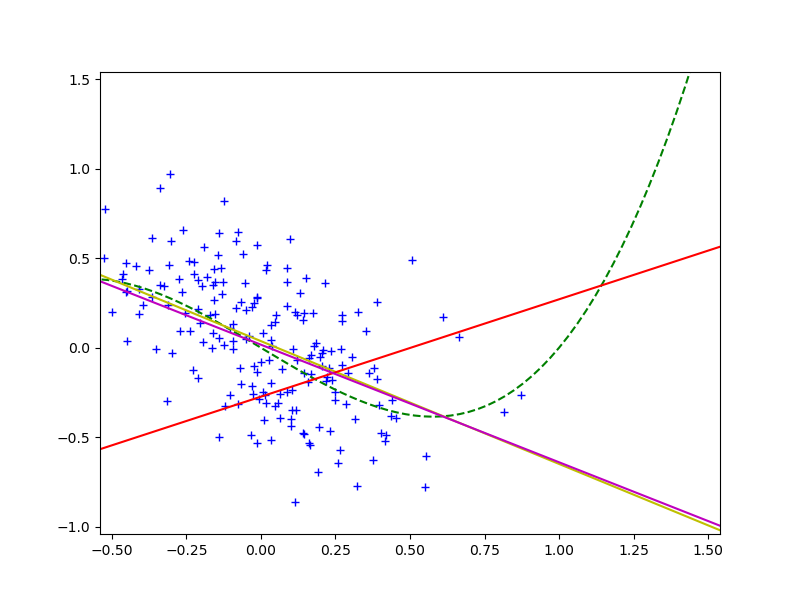
видно, что она практически совпадает с желтой, а значит мы действительно побороли covariate shift и улучшили предсказательную силу модели на проверочном наборе.

Batch Normalization. Определение.

Разобравшись с тем, что означает covariate shift, возвращаемся к статье [1]. В которой вводится понятие Internal Covariate Shift (ICS) - изменение распределения входных данных слоя нейронной сети в результате изменения параметров модели в процессе тренировки. Т.е. каждый слой нейронной сети представляет собой некую функцию, переводящую один случайный вектор в другой, на вход случайный вектор приходит из предыдущего слоя нейронной сети, соответственно, в процессе тренировки веса предыдущего слоя меняются - значит может поменяться и распределение векторов, которые предыдущий слой выдаёт. Идея BN в том, чтобы погасить этот самый ICS и за счет этого ускорить тренировку.

Мы сейчас не будем углубляться в то, насколько действительно ICS оказывает влияние на скорость тренировки, и борется ли BN с ICS. Позже мы разберем статьи, которые к идеи с ICS относятся с большим скептицизмом и объясняют успех BN совсем другим. Но то, что BN отлично работает подтверждается на практике, поэтому переходим к его описанию

Если теоретическое обоснование BN выглядит “притянутым за уши” (во всяком случае в статье нет каких-то внятных экспериментов, которые бы указывали на то, что до добавления BN сеть страдала от ICS и вот вам статистика, а после перестала, и вот вам другая статистика), то какие практические соображения лежат в основе метода, авторы описывают весьма четко и понятно.

Начинается все c известного метода преобразования случайных векторов, который называется whitening (после применения преобразования данные становятся похожи на “белый шум”) и формально определяется так: whitening - это такое линейное преобразование, которое переводит случайный вектор $X$ в случайный вектор $Y$ (той же размерности), таким образом, чтобы у получившегося вектора $Y$ все компоненты имели нулевое математическое ожидание, были некоррелированы и их дисперсии равнялись единице (иначе говоря у вектора $Y$ была бы единичная ковариационная матрица).

Пример.

Рассмотрим случайный вектор $X \in \mathbb{R}^2$ из многомерного (двумерного) нормального распределения, со средним $\mu = ( 1, 0.5 )$ и ковариационной матрицей:

\[\Sigma = \begin{pmatrix} 2 & -1.2 \\ -1.2 & 1. \end{pmatrix}\]

Сегенерируем некоторое количество векторов, подчиняющихся этому распределению и отрисуем их на плоскости:

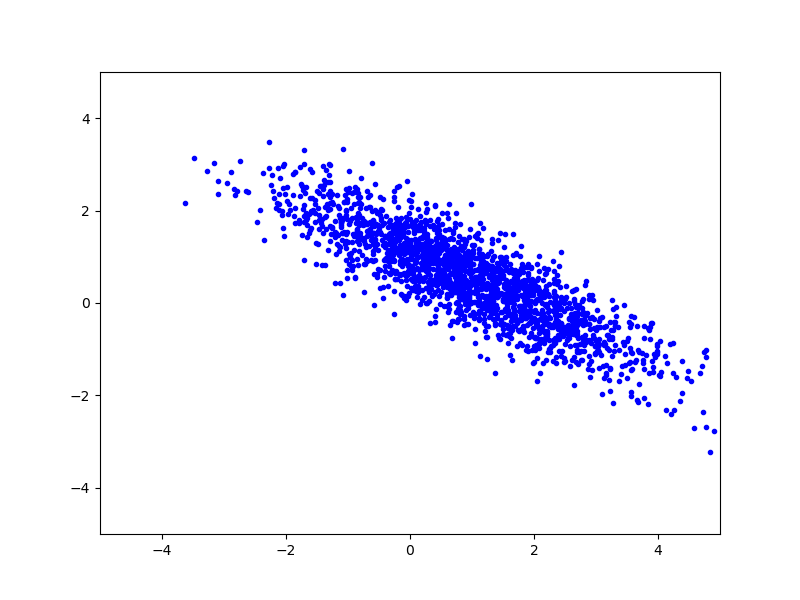
Теперь найдем собственные числа и собственные вектора для матрицы ковариации (если бы мы не знали матрицу ковариации и среднее, то могли бы вычислить приближенное значение из набора векторов):

$\lambda_1 = 2.8, e_1 = (e_{11}, e_{12}) = (0.83205029, -0.5547002)$

$\lambda_2 = 0.2, e_2 = (e_{21}, e_{22}) = (0.5547002, 0.83205029)$

Обозначим:

\[\Phi = \begin{pmatrix} e_{11} / \sqrt{\lambda_1} & e_{12} / \sqrt{\lambda_1} \\ e_{21} / \sqrt{\lambda_2} & e_{22} / \sqrt{\lambda_2} \end{pmatrix}\]

и определим линейное преобразование:

\[Y = \Phi \cdot (X - \mu)\]

Это преобразование осуществит whitening для исходного набора $X$. При этом $Y$ будет выглядить как-то так:

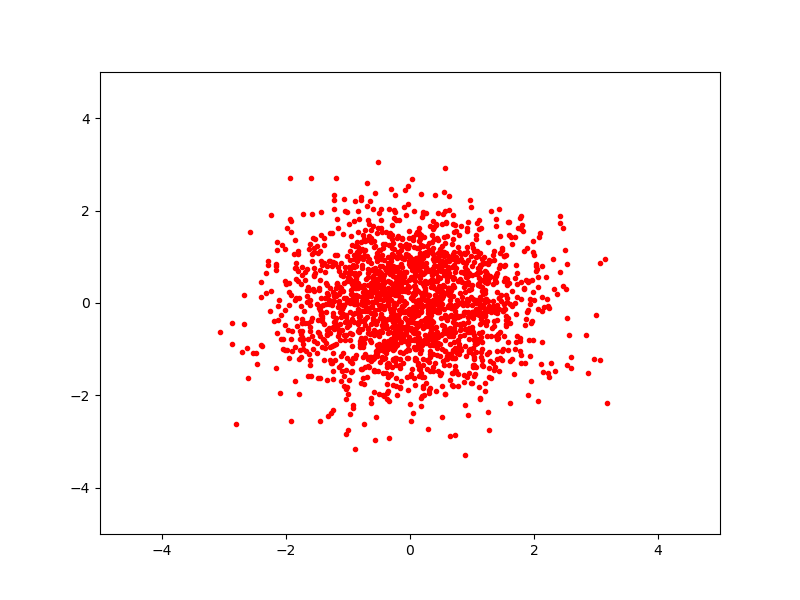
Покончили с примером, смысл того, что предполагается сделать с данными понятен.

Whitening хорошо зарекомендовал себя в том числе, когда мы тренируем нейронные сети, но обычно, при тренировке нейронных сетей он используется на исходных данных. Авторы статьи резонно замечают, что не худо было бы применить нечто похожее и на промежуточных данных, которые приходят на вход слоёв нейронной сети. Однако, возникает две проблемы. Первая, и она же основная, - это крайне дорогое удовольствие, вычислять и применять whitening преобразование для всех слоёв. Вторая, нам бы хотелось, чтобы наша сеть была дифференцируемой функцией (а иначе оптимизировать недифференцируемую функцию будет достаточно проблематично), но введение whitening преобразования дифференцируемость порушит (может и не везде, но и в одном месте будет достаточно). Поэтому предлагается несколько упростить подход и просто нормализовывать данные по каждой компоненте вектора отдельно. Т.е. для вектора $X = (x_1, …, x_d)$ посчитать математическое ожидание и дисперсию для каждой компоненты отдельно и нормализовать его в вектор $\hat X = (\hat x_1, …, \hat x_d)$, используя следующие преобразование:

\[\hat x_k = \frac {(x_k - E(x_k))} {\sqrt{Var(x_k)}}\]

Возвращаясь к только что рассмотренному примеру, нормализованные данные $\hat X$ будут выглядеть вот так:

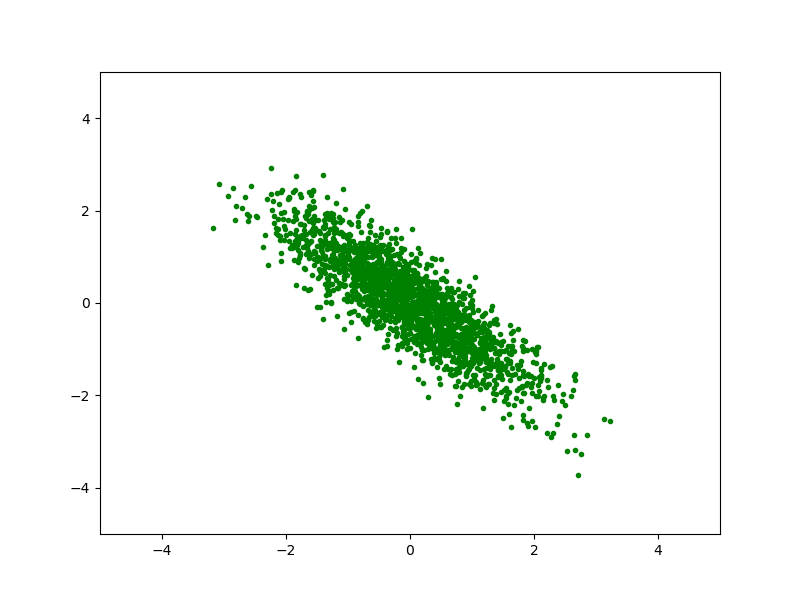
Однако, если просто нормализовывать данные подаваемые на вход слоя (некоторой функции), то мы сужаем возможности того, что слой может представлять, например, если взять в качестве функции сигмоид, то нормализация данных подаваемых на вход приводит нас в область, где сигмоид почти линейная функция. Это не хорошо, поэтому вводим два дополнительных параметра $\gamma_k$ и $\beta_k$, которые будут тренироваться вместе с остальными параметрами сети, и окончательное преобразование будет выглядеть как:

\[y_k = \gamma_k \cdot \hat x_k + \beta_k = \gamma_k \cdot \frac {(x_k - E(x_k))} {\sqrt{Var(x_k)}} + \beta_k\]

Замечание. Если мы положим $\gamma_k = \sqrt{Var(x_k)}$ и $\beta_k = E(x_k)$, то получим тождественное преобразование, т.е., в принципе, возможна ситуация, когда вводимая трансформация ничего не изменит вообще.

Итак, авторы определили преобразование $BN_{\gamma, \beta}(x)$, которое добавляется перед каждым слоем нейронной сети (или не перед каждым - это уже вопрос подбора структуры сети). При этом $\gamma, \beta$ - тренируемые параметры, и их черезвычайно много, по паре на каждую компоненту вектора на входе каждого слоя сети. Остаётся пара мелочей.

Первое, во время тренировки мы работаем не со всем тренировочными данными разом, а с данными разделенными на минибатчи. Поэтому во время тренировки мы нормализуем данные в минибатче, т.е. аппроксимируем математическое ожидание и дисперсии в преобразовании $\hat x$ по каждому минибатчу отдельно.

Второе, когда сеть используется для вывода, обычно у нас нет ни батчей ни даже минибатчей, поэтому среднее и дисперсию мы сохраняем из тренировки, для этого для каждой компоненты вектора входа каждого слоя мы запоминаем аппроксимированые математическое ожидание и дисперсию, считая скользящую среднюю математического ожидания и дисперсии по минибатчам в процессе тренировки.

Batch Normalization. Практика.

Итак, что такое BN мы определили, разберёмся как её применять. Обычно и полносвязный, и свёрточный слой можно представить в виде:

\[z = g(W\cdot x + b)\]

$W$ и $b$ - это параметры линейного преобразования, которые мы тренируем, $g(\cdot)$ - некоторая нелинейная функция (сигмоид, $ReLu(\cdot)$ и т.п.). Вставляем BN перед применением нелинейного преобразования и получается:

\[z = g(\textrm{BN}(W \cdot x))\]

Мы убрали сдвиг $b$, потому что, когда мы будем нормализовывать распределение, то $b$ всё равно потеряется, а затем его место займет сдвиг $\beta$ - параметр BN. Также в [1] авторы объясняют, почему BN не применяется непосредственно к $x$. Обычно $x$ это результат нелинейности с предыдущего слоя, форма распределения $x$ скорее всего меняется в процессе тренировки и ограничение от BN не помогут убрать covariate shift.

Чтобы получить максимальный эффект от использования BN в статье [1] предлагается еще несколько изменений в процессе тренировки сети:

1. Увеличить learning rate. Когда в сеть внедрена BN можно увеличить learning rate и таким образом ускорить процесс оптимизации нейронной сети, при этом избежать расходимости. В сетях без BN при применении больших learning rate за счет увеличения амплитуды градиентов возникает расходимость.

2. Не использовать dropout слои. BN решает в том числе те же задачи, что и dropout слои, поэтому в сетях где мы применяем BN, можно убрать dropout слои - это ускоряет процесс тренировки при этом переобучения сети не возникает.

3. Уменьшить вес $L^2$ регуляризации. $L^2$ регуляризация обычно используется при тренировки сетей, чтобы избежать переобучения. Авторы [1] уменьшили в пять раз вес $L^2$ регуляризации в штрафной функции, при этом точность на валидационных данных увеличилась.

4. Ускорить убывание learning rate. Поскольку при добавлении в сеть BN скорость сходимости увеличивается, то можно уменьшать learning rate быстрее. (Обычно используется либо экспоненциальное уменьшение веса, либо ступенчатое, и то и другое регулируется двумя параметрами: во сколько раз и через сколько итераций уменьшить learning rate, при применении BN можно сократить число итераций)

5. Более тщательно перемешивать тренировочные данные, чтобы минибатчи не собирались из одних и тех же примеров.

Резюмируя. Авторы статьи [1] предложили методику ускорения сходимости нейронной сети. Эта методика доказала свою эффективность, кроме того она позволяет применять более широкий интервал метапараметров тренировки (например, больший learning rate) и с меньшей аккуратностью подходить к инициализации весов сети. Объяснение данной методики основывается на понятии ICS, однако, каких-то существенных подтверждений того, что данный метод действительно позволяет погасить ICS и именно за счет этого улучшить процесс тренировки в статье я не нашел (возможно плохо искал). Есть только некие теоретические рассуждения, которые не выглядят (на мой взгляд) достаточно убедительно.

---

Литература

1. S. Ioffe, Ch. Szegedy, “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift”, arXiv:1502.03167v3, 2015

2. H. Shimodaira, “Improving predictive inference under covariate shift by weighting the log-likelihood function.”, Journal of Statistical Planning and Inference, 90(2):227–244, October 2000.

3. Sh. Santurkar, D. Tsipras, A. Ilyas, A. Madry, “How Does Batch Normalization Help Optimization? (No, It Is Not About Internal Covariate Shift)”, arXiv:1805.11604v5, 2019