arXiv:2003.02874v1

Практически все задачи компьютерного зрения сейчас решаются при помощи свёрточных нейронных сетей. С одной стороны это крайне позитивно сказывается на качестве решения этих задач, с другой появилась необходимость собирать большие датасеты из картинок. Картинки в датасетах в основном хранятся в jpeg формате, а поскольку этот формат сжимает в том числе за счёт потери части данных, логично задаться вопросом, как достичь баланса между размером картинок и качеством работы нейронных сетей.

Основная “потеря” данных при jpeg кодировании происходит на этапе квантизации коэффициентов DCT преобразования. За квантизацию, отвечают Q-таблицы, которые могут меняться в зависимости от реализации кодировщика. В основном эти таблицы подбираются таким образом, чтобы потеря качества картинки не была заметна человеческому глазу. Авторы статьи задались вопросом, нельзя ли подобрать такие Q-таблицы, которые помогут нейронным сетям, возможно даже в ущерб тому, как пережатая картинка будет выглядить для человека. Ну или хотя бы не понижая качества работы сетей, попытаться увеличить коэффициент сжатия алгоритма.

Для начала коротенечко пробегусь по алгоритму jpeg сжатия. Он состоит из нескольких этапов.

1. Получив на вход картинку (например, в RGB) алгоритм переводит её а YCbCr пространство, и уменьшает размеры цветовых компонент вдвое. Т.е. если у нас была картинка 640 на 640 по 24 бита на пиксел, то уже после первого этапа, мы получим три пачки данных: яркость (Y) 640 на 640 и 8 бит, и две цветности (Cb, Cr) - 320 на 320 тоже 8 бит.

2. Теперь картинка делится на блоки 8 на 8 пикселей, и к каждому из таких блоков применяется DCT преобразование. На выходе мы получаем блоки 8 на 8 байт только уже коэффициентов, которые фактически отвечают за амплитуду соответствующей частоты в исходном блоке. Например, DCT(0, 0) - это просто среднее арифметическое всех пикселей в блоке. Обычно более низкие частоты имеют большие по значению коэффициенты. Весь алгоритм сжатия с потерями строится на том факте, что высокочастотные сигналы на картинке наш глаз замечает хуже чем низкочастотные, и значит можно их немножко выкинуть, а мы и не заметим. Кстати, пиксельный шум тоже проходит по разряду высокочастотного сигнала, так что jpeg кодирование иногда может даже, в некотором смысле, улучшить картинку.

3. Вот тут и появляется Q-таблица - это блок 8 на 8 чисел, которые нужны для того, чтобы по-элементно поделить коэффициенты DCT из блоков с шага 2. А поскольку чиселки у нас исключительно целые, то многие коэффициенты не выдержав деления занулятся, а мы именно этого и добиваемся: чем больше нулей тем лучше сожмётся. Выбор Q-таблицы крайне ответственное мероприятие. Собственно, когда мы выбираем “качество сжатие” это мы как раз выбираем какой Q-таблицей нам “испортят” коэффициенты. Обычно таблицы создаются эксперементально на основе оценки результатов их применения с точки зрения человеческого восприятия.

На этом воспоминания про jpeg заканчиваем, все остальные этапы кодирования нас не интересуют, переходим к статье.

Авторы берут сетку ResNet50 натренированную для классификации, и хотят проверить, как меняется качество классификации в зависимости от качества jpeg картинок в тестовом датасете. Тестовые датасеты берутся из ImageNetV2, эти тестовые датасеты уже состоят из пожатых jpeg-ом картинок, но плюс в том, что есть код, который эти картинки сгенерировал и ссылки на фотографии гораздо большего размера из которых датасет собирался. Взяв большие фотографии, авторы статьи масштабируют их вниз, это масштабирование сглаживает jpeg артефакты исходной картинки и теперь у них есть набор аналогичный тестовому набору ImageNetV2, только без потери качества картинок. Можно использовать разные Q таблицы для сжатия и после прогонять на результате ResNet и следить за изменением качества классификации. В тестовом наборе 1000 классов по 10 изображений для каждого класса. Чтобы ускорить процесс авторы берут только 500 классов по 5 изображений и работают с ними (но в конце дополнительно приводят данные и на полном наборе). Качество классификации меряется как Top-1 точность, а коэффициент сжатие как отношение размера исходной картинки (ширина * высота * 3) байта к результирующему jpeg-у.

Фактически задача состоит в подборе “хорошей” Q таблицы, чтобы либо размер jpeg получался меньше, а классификация не ухудшалась, либо размер оставался прежним, а качество классификации росло. Q таблица представляет из себя 8 * 8 = 64 байта, т.е. всего вариантов таблиц получается 256 в степени 64, это что-то около единицы со 154 нулями и перебрать их все, чтобы выбрать лучшую, не представляется реальным на данном этапе развития компьютерной техники. Поэтому авторы используют следующие методики.

Случайный поиск с сортировкой

Исходя из того, что низкии частоты важнее высоких, логично предложить следующую стратегию:

1. Зададимся некоторыми пределами s и e, s < e и оба находятся между 1 и 255 включительно

2. Выбираем 64 числа в пределах от s до e случайным образом.

3. Упорядочим эти числа по возрастанию и соберём из них Q таблицу обычным zig-zag-ом:

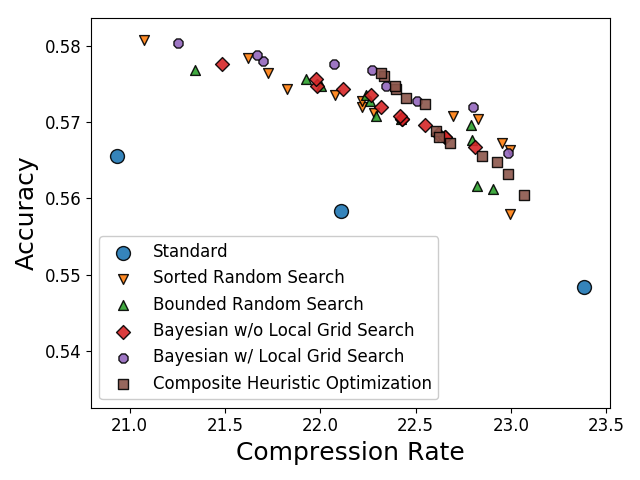
Такую стратегию получения кандидатов авторы называют sorted random search. Они выбрали таким образом 4’000 Q-таблиц, подсчитали для них коэффициент сжатия, и точность классификации, а затем сравнили с 1’000 Q-таблиц выбранных случаным образом (т.е. без пересортировки элементов), а также стандартными Q-таблицами jpeg кодировщика.

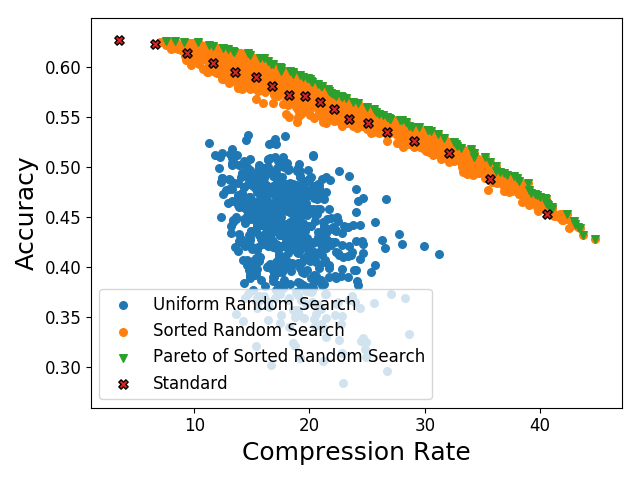
Выбрав оптимальные по Паретто точки для случайного поиска с сортировкой, авторы получили улучшение 1-2% качества классификации при фиксированном коэффициенте сжатия и от 10% до 200% увеличение сжатия при фиксированной точности классификации, относительно стандартных Q-таблиц.

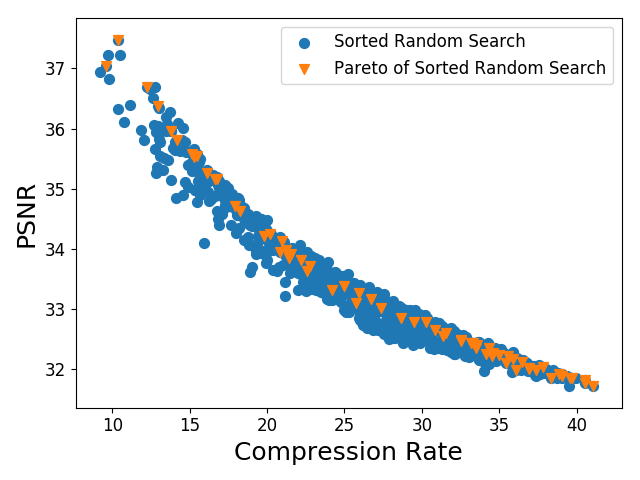
Чтобы показать, что качество классификации и метрика похожести картинки PSNR не одно и тоже (а выбирая стандартные Q-таблицы обычно ориентируются в том числе на PSNR) авторы построили график зависимости PSNR от коэффициента сжатия и отметили на нем оптимальные по Парето точки для качества классификации.

Ограниченный поиск

Случайный поиск с сортировкой выбирает из широкого множества таблиц, при этом накладывая ограничения упорядоченности. Следующим шагом, авторы хотят сократить пределы в которых может выбираться каждый элемент Q-таблицы и при этом избавится от требования упорядоченности, предполагая, что возможно это позволит улучшить качество результатов. Они фиксируют jpeg-качество равным 50, в этом случае коэффициент сжатия в среднем получается равным 22.

Тут я несколько не уверен, что правильно разобрался. Принцип понятен, авторы берут некоторое множество Q-матриц отвечающих коэффициентам сжатия от 21 до 23. Для каждой позиции в Q-матрице получается набор элементов, из такого набора находят минимальное и максимальное значения, и расширяют этот предел еще на половину среднеквадратичного отклонения для данного набора. Таким образом, мы имеем некие отрезки из которых теперь случайным образом выбираем элементы матрицы. Не до конца понятен, только выбор исходного множества матриц, похоже это множество отвечающих точкам оптимальным по Парето из прошлого пункта.

Теперь мы ограничили область поиска и авторы предлагают применить следующии алгоритма поиска оптимальной матрицы.

Bounded Random Search

Просто случайный поиск, т.е. элементы матрицы выбираются равновероятно в заданных для них пределах.

Bayesian Optimization

Поскольку оптимизируемая функция тяжело вычислима авторы решили использовать метод баесовой оптимизации. Но тут нужна одна оптимизируемая функция, а до сего момента их было две: коэффициент сжатия и точность классификации. Поэтому авторы взяли кривую из оптимальных по Парето точек, полученных случайным поиском с сортировкой, и аппроксимировали эту кривую при помощи параболы. SRSPareto = a * CompressionRate * CompressionRate + b * CompressionRate + с, и в качестве целевой функции выбрали y = Accuracy - SRSPareto(CompressionRate)

Далее они ограничили область интереса только низко- и средне- частотными коэффициентами, т.е. коэффициентами из Q-таблицы, лежащими строго выше главной диагонали. И 20 раз повторили следующую процедуру:

1. Выбираем случайным образом 100’000 таблиц с ограничениями на элементы, аналогичными bounded random search

2. Оставляем таблицу с максимальным значением целевой функции.

3. Выбираем случайным образом в таблице пять позиций из области интереса.

4. Осуществляем поиск по решетке для пяти элементов выбранных на шаге 3

Оставляем таблицу с максимальным значением целевой функции.

Composite Heuristic OptimizationНесколько разных стратегий поиска оптимума применяются комплексно. Выбор стратегии осуществляется на основе алгоритма многорукого бандита.Углубляться не буду, собственно, авторы тоже не углубляются. Да и какого-то существенного прироста этот подход всё равно не даёт.### Результаты применения всех методов: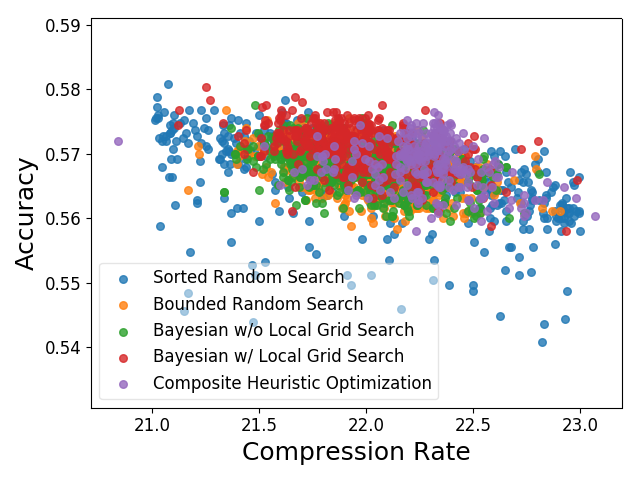

Точки оптимальные по Парето:

Вывод

1. Авторы подбирали таблицы только на части тестового датасета, но пересчитали показатели с оптимальными Q-таблицами полученными разными методами, и на полном наборе. Действительно, оказалось, что можно несколько повысить качество классификации (практически на 1%) не увеличивая размера хранимых данных.

2. Хорошее качество по PSNR метрике не одно и тоже, что хорошее качество для классификационной сети

3. Самое прекрасное, что в сложных методах нет особого смысла, простой случайный поиск с ограничением на сортировку элементов отлично работает. Качество плюс-минус такое же как у сложных способов, но скорость подбора в разы выше.