arXiv:1807.03247

Одно из свойств свёрточных сетей, которое позволяет им хорошо решать массу разнобразных задач компьютерного зрения, например, задачи классификации, это инвариантность относительно сдвига картинки. Однако, это же свойство мешает в других задачах. В данной работе авторы рассматривают несколько простых модельных задач, с которыми обычные свёрточные сети не справляются. А именно, получив на вход черную картинку с одним белым пикселем вернуть координаты этого пикселя, или, обратная задача, сгенерировать изображение, где на черном фоне будет отрисована белая точка в заданных координатах (или белый квадрат с центром в этих координатах).

В качестве решения авторы предлагают добавить в сеть CoordConv слои. Но прежде чем начать разговор про CoordConv разберемся с задачами и датасетом.

Датасет

Авторы предлагают Not-so-Clevr датасет, на котором они планируют провести первые эксперименты. Датасет состоит из чернобелых изображений размера $64 \times 64$, с черным фоном и одним белым квадратом $9 \times 9$, поскольку требуется, чтобы квадрат всегда был полностью внутри изображения, то центр квадрата может иметь $56 \times 56$ вариантов позиционирования, иначе говоря наш датасет содержит 3’136 примеров. Каждый элемент датасета можно представить в виде тройки:

1. $C_i \in \mathbb{R}^2$ - позиция центра квадрата $(x, y)$,

2. $P_i \in \mathbb{R}^{64 \times 64}$ - one-hot представление позиции центрального пикселя квадрата, или, что тоже самое, черно-белое изображение - черное поле с белой точкой в пикселе центра квадрата,

3. $I_i \in \mathbb{R}^{64 \times 64}$ - черно-белое изображение с отрисованным квадратом.

Предлагается два разбиения датасета на тренировочную и тестовую части. Равномерное - все позиции центра квадрата случайным образом разбиваются в соотношении 80/20. И квадрантами - три из четырёх квадрантов отправляются в тренировочную часть и один в тестовую (на всякий случай, уточним - здесь соотношение 75/25). Для понимания, две картинки из статьи

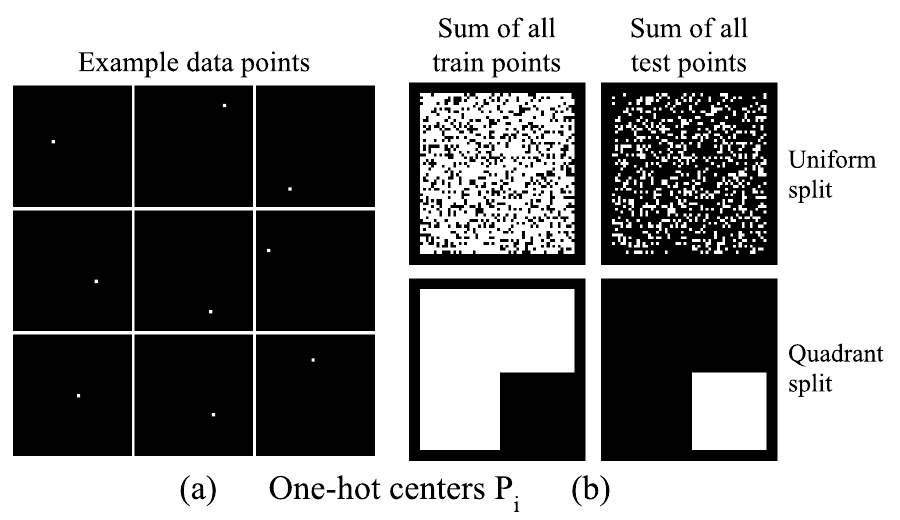
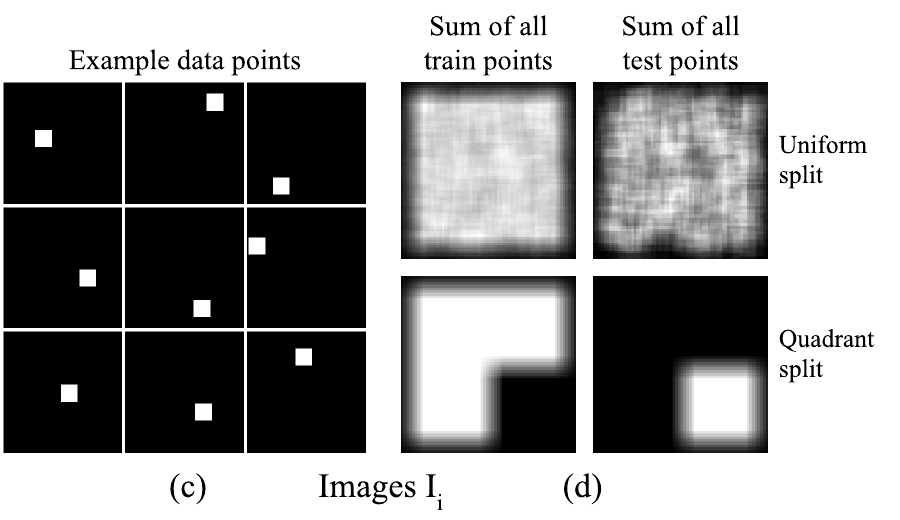
Задачи

Авторы предлагают решать три задачи:

1. Классификация координат с учителем - по заданным координатам восстановить элемент $P_i$ - one-hot представление позиции. И задача обратная к данной регрессия координат - получить по изображению $P_i$ координаты единственной белой точки на чёрном изображении.

2. Отрисовка с учителем - по заданным координатам восстановить элемент $I_i$ - отрисовать квадрат с центром в заданной позиции.

3. Отрисовка без учителя (GAN) - по заданному случайному вектору отрисовать синий круг и красный прямоугольник.

Свёрточный координатный слой

Картинка и данные на выходе промежуточных свёрточных слоёв представляются в виде тензора $\mathbb{R}^{w \times h \times c}$, после чего снова проходят через очередной свёрточный слой. Авторы предлагают добавить в этот тензор еще два канала (или три), причем можно это сделать непосредственно в исходное изображение или в некоторый произвольный, промежуточный тензор особенностей. Первый добавляемый тензор $i$ содержит в ячейке индекс строки в которой находится эта ячейка:

\[i = \begin{bmatrix}0 & 0 & ... &0\\1 & 1 & ... & 1\\ \vdots & \vdots & ... & \vdots\\ h-1 & h-1 & ... & h-1\end{bmatrix}\]

второй тензор $j$ содержит соответственно номер столбца:

\[j = \begin{bmatrix}0 & 1 & ... &w-1\\0 & 1 & ... & w-1\\ \vdots & \vdots & ... & \vdots\\ 0 & 1 & ... & w-1\end{bmatrix}\]

Прежде чем прикрепить эти каналы к тензору авторы масштабируют их, чтобы значения попали в отрезок $[-1, 1]$. Например, для тензора $i$:

\[i = i \cdot \frac 2 {h-1} - 1\]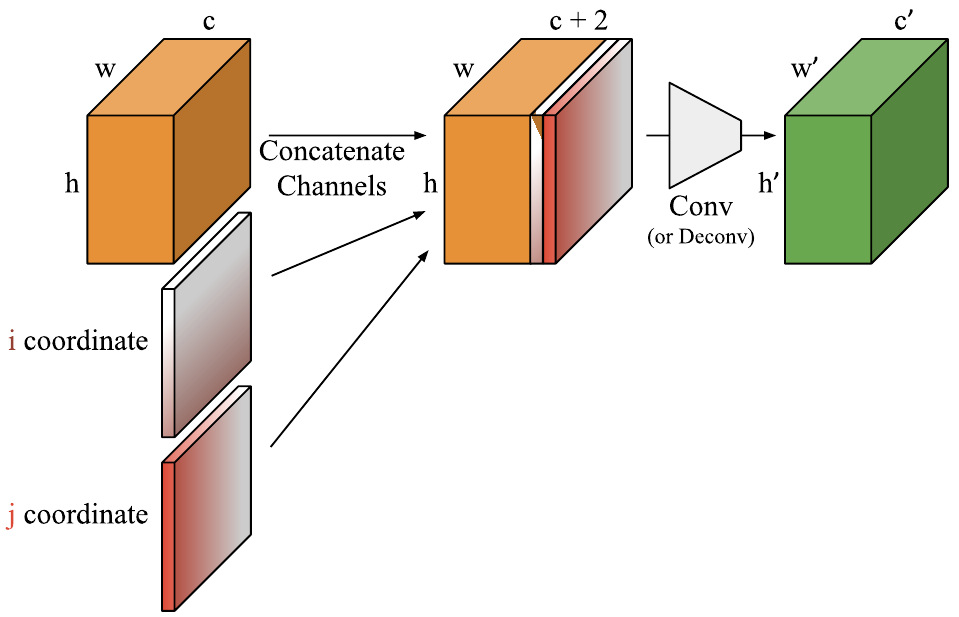

Также авторы пишут о том, что в некоторых эксперементах они с пользой применяли тензор, содержащий “расстояние до центра”, т.е. с элементами $r = \sqrt {(i - h / 2)^2 + (j - w / 2)^2}$ снова отмасштабированными в отрезок $[-1, 1]$.

Количество параметров

Для обычного свёрточного слоя (не рассматривая свободный член) с ядром размера $k$, входным числом каналов $c$ и выходным - $c’$ определены $cc’k^2$ весов, которые требуется натренировать. При добавлении двух или трех координатных слоёв на вход, количество весов увеличится соответственно до $(c + 2)c’k^2$ или до $(c + 3)c’k^2$. Очевидно, что количество параметров не сильно возрастает и можно этот рост погасить просто убавив количество входных каналов на тоже число.

Инвариантность к сдвигу

Если начальные веса свёрток, воздействующих на координатные каналы инициализировать нулями, то свойство свёрточной сети - инвариантность к сдвигам сохранится. Но на самом деле, координатные слои есть смысл использовать при решении задач, где нарушение инвариантности к сдвигу вытекает из самой задачи. Собственно, когда мы присоединяем к последнему свёрточному слою полносвязные слои мы как раз тоже решаем задачу в условиях которой нет инвариантности к сдвигу, однако, полносвязный слой намного более существенно увеличивает количество потребных к тренировки весов.

Решение задач обучения

Первая задача, это отрисовка пикселя по координатам $(x, y)$, можно считать это задачей классификации, если каждый пиксель изображения рассматривать как класс. Авторы пробуют оба варианта разбиения датасета на тренировочную и тестовую части (равномерную и по квадрантам). Для простой свёрточной сети получается более или менее натренировать вариант в случае равномерного разбиения (максимально 86% качества), для варианта одного квадранта отнесенного в тестовый набор целиком, стандартная свёрточная сеть не обобщается совсем. Новый вариант сети с координатными слоями, во-первых, значительно лучше по качеству (т.е. добрал 100% на обоих вариантах разбиения датасета), во-вторых, существенно быстрее этого качества достигает (соотношение: часы тренировки обычной свёрточной сети и десятки секунд для варианта с координатными слоями) и, наконец, делает это всё при помощи сети с на порядок меньшим количеством весов (а это, как замечают авторы статьи, говорит о том, что модель с координатными слоями лучше описывает данную задачу).

Для сравнения результаты работы двух вариантов свёрточных сетей с координатными слоями и без:

С обратной задачей - регрессией координат отмеченного пикселя ситуация схожая. Авторам удалось натренировать обычную свёрточную сеть, чтобы она обобщилась для случая равномерного разбиения датасета, но эта сеть не работает для случая разбиения датасета квадрантами. Используя полносвязную сеть авторы получили качество порядка 5 пикселей ошибки в среднем, для датасета разделенного квадрантами, но эта сеть плохо работает для равномерно разделенного датасета.

Вариант с координатными слоями снова показал отличный результат, испльзуя при этом `существенно меньшее количество параметров.

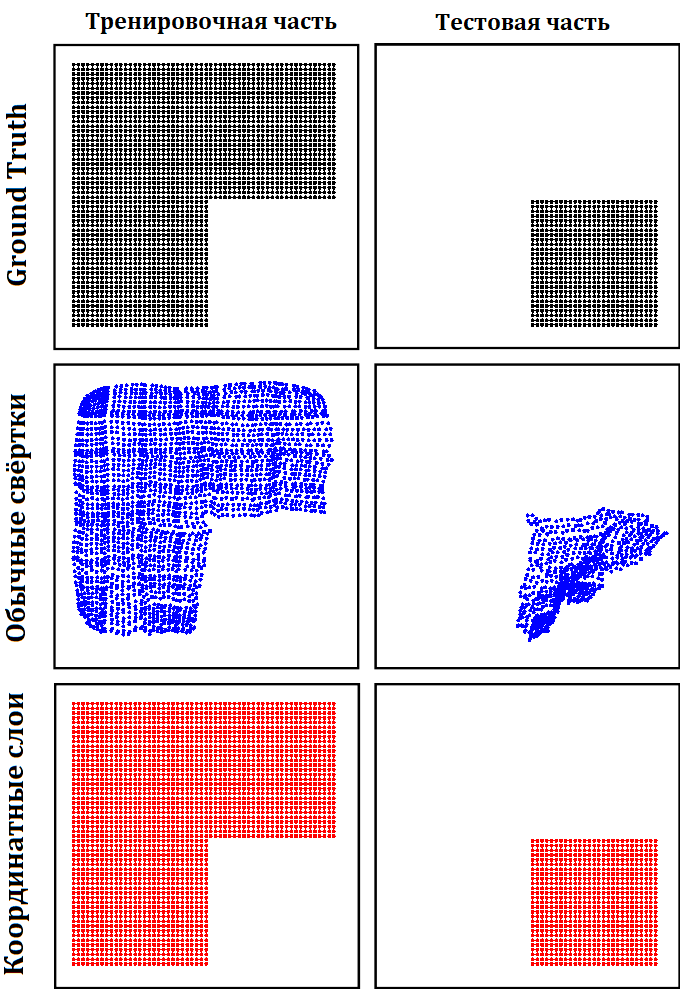
Задача отрисовки квадрата в нужных координатах снова показала преимущества координатных слоёв. Если в случее равномерного разбиения датасета, обычная сеть работает хуже, чем сеть с координатными слоями, но в целом показывает достаточно не плохой результат:

то в случае разбиения датасета квадрантами обычной сети снова не удаётся хорошо обобщиться:

Следующая задача натренировать GAN для генерации изображений. Авторы снова используют для тестов простую моделбьную задачу: сгенерировать изобраение. которое содержит две геометрических фигуры одну синего другую красного цвета. В этой задачи использование координатных слоёв тоже показывает хорошие результаты.

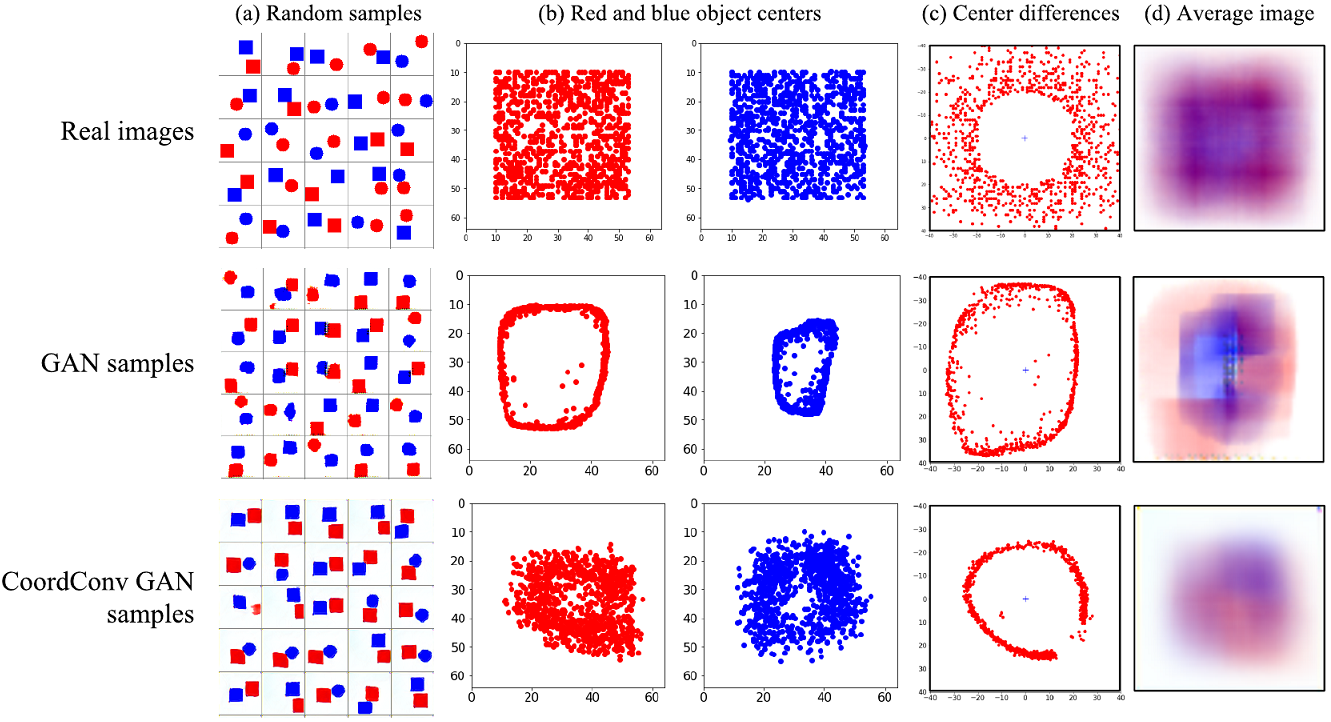
Во-первых, в новом подходе генерируются картинки на которых объекты распределены более равномерно, в случае обычного свёрточного GAN видно, что центры объектов расположены в основном на некоторой одномерной кривой. При этом и старая и новая модель плохо справляется с разнесением центров объектов на случайное расстояние. Ну и наконец усредненное изображение в случае использования координатных слоёв выглядит более сглаженным, хотя и нельзя сказать о достижении идеала.

Авторы пишут, что они так же проверили подход на классификации изображений - измеримого улучшения не принесло. И на задаче детектирования объектов, на MNIST объектах раскиданных по большому изображению - получили существенное улучшение IoU теста для Faster R-CNN сети.

В статье есть еще некоторое количество познавательной информации, в том числе описание структуры сетей (свёрточных и с координатными слоями), которые использовались в эксперементах, также авторы собрали свои наработки в репозиторий на github.