arXiv:1607.00653

Графы дело известное и часто используется в компьютерных науках для представления данных. Одной из задач на графах является задача предсказания свойств вершин графа (например, если рассматривать социальные сети, то полезно уметь предсказывать интересы пользователей, опираясь на их связи с другими пользователями). Другая задача находить не учтённые связи между вершинами (в тех же социальных сетях определять, например, знакомы ли люди в реальной жизни). Один из подходов к решению задач такого рода это “вкладывание” вершин графа в некоторое многомерное векторное пространство и затем определение близости вершин исходного графа как близость соответствующих им векторов.

Авторы статьи как раз рассказывают о том, как такое вложение осуществить

Самый “простой” способ - это определить алгоритм высчитывания особенностей (т.е. компонент вектора) вручную, опираясь на знание предметной области. Но в этом случае алгоритм будет жестко привязан к конкретным условиям и их изменение повлечет за собой необходимость придумывать новый алгоритм. В статье предлагается более общий подход. А именно, научиться “подбирать” функцию, вкладывающую вершины графа в векторное пространство, решая задачу оптимизации. При этом ничего кроме графа (т.е. набора вершин и ребёр, возможно взвешенных) не используется, а значит этот подход может применяться как для социальных сетей, так и для задач в области генетики и где угодно еще.

Формализуя, получается следующие. Пусть у нас есть граф $\mathcal G = (\mathcal V,\mathcal E)$ (ориентированный или не ориентированный, взвешенный или нет). Задача: построить функцию $f : \mathcal V \rightarrow \mathbb{R}^d$, которая отображает вершины графа в некоторое векторное пространство размерности $d$. Поскольку вершин у нас конечное число, эту функцию можно даже представить в виде таблицы размера $|\mathcal V| \times d$.

Первым делом для каждой вершины $u \in \mathcal V$ определим окрестность $N_S(u) \subset \mathcal V$, которая получена в результате сэмплирования по стратегии $S$.

Функцию будем искать, решая задачу оптимизации:

\[\max_f \sum_{u\in \mathcal V} \log(Pr(N_S(u)|f(u))\]

т.е. мы должны подобрать функцию так, чтобы максимизировать условную вероятность наблюдать правильную окрестность вершины $u$ в силу представления этой вершины функцией $f$. Авторы предлагают ряд стандартных допущений, чтобы задачу можно было решить:

1. Независимость. Т.е. вершины в окрестность $u$ попадают независимо и

   \[Pr(N_S(u) | f(u)) = \prod_{n_i \in N_S(u)} Pr(n_i | f(u))\]

2. Симметричность пространства особенностей. Т.е. $Pr(n_i \vert f(u)) = Pr(u \vert f(n_i))$. Поэтому вероятность предлагается записывать в форме:

   \[Pr(n_i | f(u)) = \frac {\exp(f(n_i) \cdot f(u))} {\sum_{v\in \mathcal V} \exp(f(v) \cdot f(u))}\]

Таким образом целевая функция будет выглядеть следующим образом:

\[\max_f \sum_{u\in V} \left( -\log Z_u + \sum_{n_i \in N_S(u)} f(n_i) \cdot f(u)\right)\]

здесь $Z_u = \sum_{u\in \mathcal V}\exp(f(n_i) \cdot f(u))$ сложно считать на больших графах, поэтому авторы планируют её аппроксимировать семплированием негативов.

Методика очень похожа на skip-gram подход в работе с задачами обработки текстов. Однако, в задачах связанных с текстами окрестность $N_S(u)$ выбирается естественным образом, просто сдвигом окна определенной ширины. В случае вершины графа, такого простого и естественного способа сэмплирования нет. Более того стратегия семплирования $S$ оказывает существенное влияние на то, какую функцию $f$ мы в итоге получим.

Обычно в графах есть две стратегии обхода, которые в данной задаче можно использовать в качестве стратегий выбора вершин в окрестности данной. Причем эти две стратегии в некотором смысле представляют два крайних варианта:

1. Поиск в ширину (Breadth-first sampling (BFS)) - в этом случае окрестность вершины ограничивается вершинами непосредственно связанными с исходной.

2. Поиск в глубину (Depth-first sampling (DFS)) - окрестность вершины содержит последовательность вершин на всё большем расстоянии (в смысле кратчайшего пути по графу) от исходной.

Рассмотрим пример:

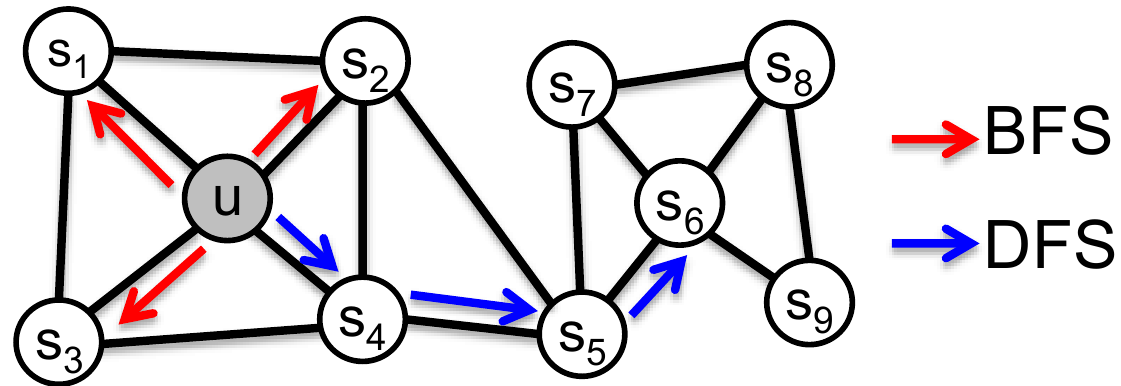
В качестве базовой вершины возьмем $u$ и ограничим размер окрестности $k = 3$. Тогда для BFS стратегии получаем $N_{BFS}(u) = \{s_1, s_2, s_3\}$, а для DFS: $N_{DFS}(u) = \{s_4, s_5, s_6\}$.

Авторы отмечают интересную особенность этих стратегий семплирования. В задачах предсказания на вершинах графа, часто выделяют два вида “одинаковости” вершин: групповая и струтурная эквивалентность. Групповая - это близость вершин находящихся в одном кластере или, иначе говоря, сильно связанных между собой рёбрами. Например, на картинке выше вершины $s_1$ и $u$ обладают свойством групповой близости. С другой стороны, структурная эквивалентность - это близость вершин, которые выполняют похожие структурные роли в графе. Например, на рисунке выше, вершины $u$ и $s_6$ являются узловыми вершинами кластеров и, следовательно, их можно считать структурно эквивалентными.

В реальных задачах предсказания на графе важно уметь выявлять и ту и другую эквивалентности.

Две стратегии семплирования (BFS и DFS) в некотором смысле реализуют два варианта выбора эквивалентности. BFS - делает локальный слепок вокруг вершины и, следовательно, позволяет для двух структурно эквивалентных вершин получить похожие отклики. DFS наоборот может набрать в окрестность вершины достаточно далекие от данной, что позволяет определять групповые свойства.

Авторы предлагают алгоритм, который позволяет параметризовать выбор стратегии семплирования между двумя крайними вариантам BFS и DFS.

node2vec

Выбрав некоторую вершину $u$ мы реализуем из нее случайный обход длины $l$: $u=(c_0, c_1, …, c_{l-1})$ определив вероятность выбора следующей вершины в виде функции:

\[P(c_i = x | c_{i-1} = v) = \begin{cases} \frac {\pi_{vx}} Z, & (x,v) \in \mathcal E\\ 0& (x,v), \notin \mathcal E \end{cases}\]

здесь $\pi_{vx}$ - ненормированная вероятность перехода из вершины $v$ в вершину $x$, а $Z$ - нормализующая постоянная. Самый простой выбор вероятности перехода это приписать $\pi_{vx} = w_{vx}$ - весу ребра между вершинами (или единице для невзвешенного графа). Однако, это не позволяет выявлять структурные особенности и как-то параметризовать разные типы окрестностей. Поэтому авторы предлагают ввести коэффициент $\alpha_{pq}(t, x)$ и определить $\pi_{vx} = \alpha_{pq}(t, x) \cdot w_{vx}$. Коэффициент использует два наперед заданных параметра $p$ и $q$, определяющих стратегию, и зависит, от вершины $t$ из которой мы попали в вершину $v$:

\[\alpha_{pq}(t, x) = \begin{cases} \frac 1 p, & d_{tx} = 0\\ 1, & d_{tx} = 1\\ \frac 1 q, & d_{tx} = 2\\ \end{cases}\]

здесь $d_{tx}$ - кратчайший путь из вершины $t$ в вершину $x$, очевидно он может принимать только три значения $\{0, 1, 2\}$. Поясняющий рисунок:

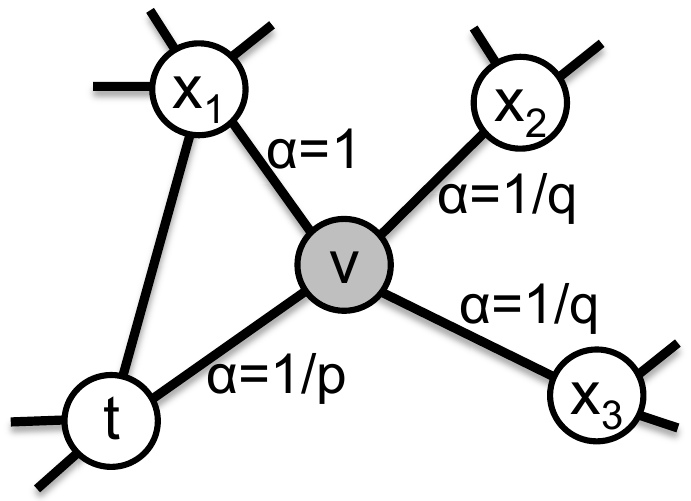
Регулируя параметры $p$ и $q$ мы можем перемещать нашу стратегию между BFS и DFS. Остановимся на этом подробнее.

1. Параметр $p$ отвечает за то насколько быстро (а значит часто) мы будем возвращаться в уже пройденные вершины. Если положить $p > \max \{q, 1\}$, то вероятность сразу же вернуться в ту вершину откуда пришли, будет меньше, чем вероятность продолжить движение в другие вершины (если, конечно, мы не зашли в тупиковую вершину и кроме как обратно идти некуда). Это как бы подталкивает нашу стратегию к DFS. С другой стороны если взять $p$ достаточно малым, то это приведет к ситуации, когда мы будем возвращаться в только что посещенную вершину и значит бродить в локальной окрестности исходной $u$.

2. Параметр $q$ в свою очередь позволяет регулировать вероятность “выхода во вне”. Если $q > 1$, то мы скорее перейдем к вершине близкой к $t$, т.е. той для которой расстояние $d_{tx} = 1$, что приводит нас к стратегиям близким своим поведением к BFS, в том смысле, что вершины беруться в локальной окрестности. Наоборот, если $q < 1$, то повышается вероятность посетить вершины удалённые от $t$ из которой мы пришли, что похоже на поведение при стратегии DFS, но не полностью совпадает с ним, потому что в данном случае мы не будет строго увеличивать расстояние до исходной вершины $u$ из которой начался обход.

Наконец, заметим, что определенная таким образом вероятность реализует марковский процесс, поскольку зависит только от прошлого (причем всего на один ход назад).

Авторы отмечают, что такой алгоритм получения окрестности вершины, кроме всего прочего достаточно эффективен и по расходу памяти, и по скорости. По памяти понятно всё равно получается $O(|\mathcal V| + |\mathcal E|)$, но во всяком случае линейно. Для оптимизации по скорости авторы предлагают генерировать случайные обходы длины $l > k$ ($k$ - количество семплов в окрестности), каждый такой обход сгенерирует окрестность для $l-k$ вершин за раз, это допустимо в силу марковской природы процесса.

Например, для графа из первого рисунка, сгенерировав случайный обход $(u, s_4, s_5, s_6, s_8, s_8)$ длины $l = 6$ мы получим три окрестности для $k=3$:

1. $N_S(u) = \{s_4, s_5, s_6\}$,

2. $N_S(s_4) = \{s_5, s_6, s_8\}$,

3. $N_S(s_5) = \{s_6, s_8, s_9\}$.

Авторы отмечают, что такое деление обхода, может привести к некоторым сдвигам в вероятностном распределении, но этим можно принебречь в силу серьезной оптимизации процесса.

Собственно, на этом можно закончить, семплировать окрестности мы научились, осталось применить SGD и выбрать оптимальную функцию $f$. Далее в статье приводится некоторое количество экспериментов для того, чтобы показать эффективность предложенного подхода, но их мы рассматривать не будем.

Реализация от авторов статьи: node2vec.