Поиск особых точек и их дескрипторов - обучение без учителя.
В задачах SfM и не только, крайне полезно уметь выделять на изображении особые точки и приписывать им некий вектор-дескриптор. Тогда, сопоставив такие точки на двух изображениях, можно определить параметры преобразования гомографии одного изображения в другое, потом найти фундаментальную матрицу и т.п.
Раньше для поиска таких точек использовались разнообразные алгоритмы типа SIFT, SURF, FAST, ORB, а теперь, как и для многих других задач компьютерного зрения, предлагается применить нейронную сеть. Т.е. авторы хотят натренировать такую сеть, чтобы подав ей на вход изображение, на выходе мы бы получили набор особых точек этого изображения с приписанными этим точкам дескрипторами.
Как и обычно, проблема с нейронными сетями ровно одна - где взять соответствующий задаче датасет. И в данном случае разметка такого рода датасета, во-первых, сложноформализуемая задача, т.е. не всегда понятно какие именно точки на изображении следует размечать как особые. Во-вторых, требует огромное количество ресурсов. Поэтому статья, в первую очередь, интересна подходом, при помощи которого авторы умудряются натренировать сеть (и получить датасет), используя только синтетические данные.
Структура сети
Сеть, которую планируют использовать для решения задачи, схематично выглядит следующим образом:
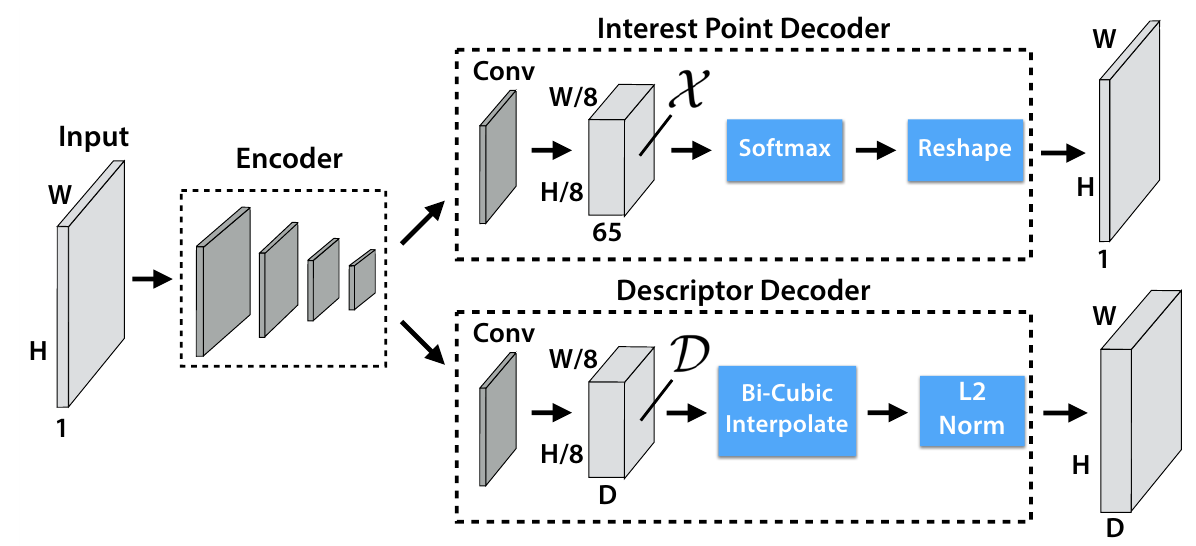
Всё достаточно тривиально, вначале изображение сворачивается до карты особенностей, используя свёрточную сеть типа VGG. При этом из одноканального изображения $W \times H \times 1$ получается тензор $W / 8 \times H / 8 \times F$. Далее обработка идёт по двум веткам, в первой ветке выбираются особые точки, во второй вычисляются их дескрипторы.
Детектор особых точек
В этой ветке тензор $W / 8 \times H / 8 \times F$ сворачивается в тензор $W / 8 \times H / 8 \times 65$, т.е. каждому тайлу $8 \times 8$ исходного изображения ставится в соответствие вектор из $65$ компонент, который потом превращается при помощи преобразования softmax в вектор вероятностей, того что соответствующая точка тайла особая (или, что особых точек нет совсем, для этого используется дополнительная 65-я компонента вектора). Теперь, если вектор развернуть обратно в тайл $8 \times 8$ и собрать все тайлы у нас получится некая “тепловая карта”, такого же размера как исходное изображение, на которой будут “подсвечены” особые точки.
Генератор дескрипторов
Вторая ветка, получив на вход тот же вектор особенностей $W / 8 \times H / 8 \times F$ сворачивает его в тензор $W / 8 \times H / 8 \times D$. Здесь $D$ - размерность вектора-дескриптора особых точек. Затем при помощи бикубической интерполяции расширяет тензор до размеров исходного изображения, и наконец, выполняет L2-нормализацию, чтобы вектор дескриптор имел единичную норму.
Тренировка и штрафная функция
Поскольку нам надо не только научиться искать особые точки, но и генерировать близкие дескрипторы для одной и той же точки на двух изображениях, то во время тренировки на вход сети изображения подаются парами. Берётся изображение с размеченными особыми точками (как получаются эти изображения и точки чуть ниже), выбирается случайное преобразование гомографии $\mathcal{H}$ и генерируется второе изображение, связанное с первым этим преобразованием. Теперь мы хотим минимизировать штраф на паре этих изображений. Штрафная функция состоит из трёх слагаемых, два отвечают за поиск особых точек, и третье за близость пар дескрипторов одной точки на разных изображениях
\[\mathcal{L(X_1, Y_1, D_1, X_2, Y_2, D_2)} = \mathcal{L_p(X_1, Y_1)} + \mathcal{L_p(X_2, Y_2)} + \lambda \mathcal{L_d(D_1, D_2)}\]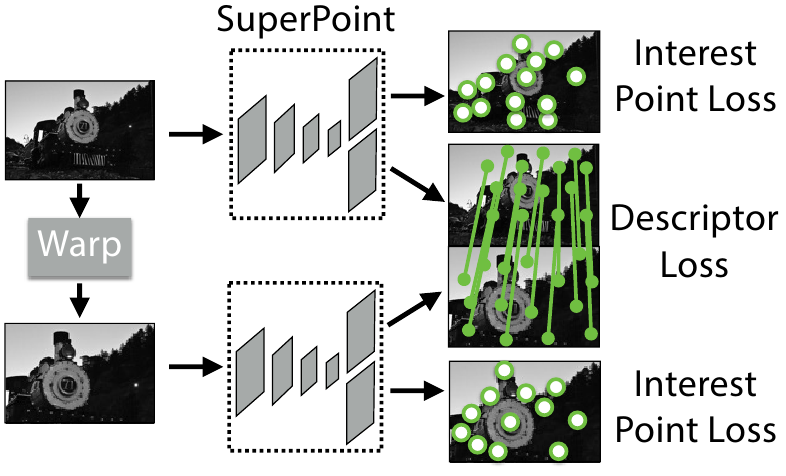
Чтобы расcчитать для изображения штраф за детектирование особых точек $\mathcal{L_p(X_i, Y_i)}$, возьмем результат работы сети из первой ветки, сразу после применения softmax, это будет тензор размера $W / 8 \times H / 8 \times 65$. Имея размеченные особые точки, сформируем такой же ground truth тензор. Для этого разобьём изображение на тайлы $8 \times 8$ и для каждого тайла получим вектор размерности $65$, все координаты которого, кроме одной, равны нулю, а единственная равная единице соответствует особой точке в этом тайле. Если особой точки нет, то единице будет равна $65$-ая координата вектора.
Если в тайл попадает несколько особых точек, то авторы предлагают выбрать одну случайным образом и для нее выставить в векторе единичку.
Теперь у нас есть $\frac W 8 \cdot \frac H 8$ пар векторов. Cчитаем для каждой пары кросс-энтропию и суммируем. Это и будет штраф детектора особых точек на изображении $\mathcal{L_p(X_i, Y_i)}$, а учитывая, что мы тренируемся на паре изображений таких штрафов будет два.
Дескрипторы мы берём из второй ветки сети - тензор до билинейной интерполяции. Т.е. дескриптор определен для тайла $8 \times 8$ изображения, а не для каждой точки. Поскольку преобразование гомографии при помощи которого связаны изображения нам известно, мы можем для каждой пары тайлов $(t_1, t_2)$ определить функцию:
\[s(t_1, t_2) = \begin{cases} 1, & ||\mathcal{H}(p_1) - p_2|| \le 8\\ 0, & otherwise \end{cases}\]здесь $p_i$ - координаты центра $i$-го тайла.
Теперь суммируем по всем парам тайлов:
\[\mathcal{L_d(D_1, D_2)} = \left(\frac {64} {W \cdot H}\right)^2 \sum_{t_1}\sum_{t_2} l_d(d_{t_1}, d_{t_2})\]здесь $d_t$ - вектор дескриптор тайла $t$, а в качестве функции штрафа hinge loss:
\[l_d(d_{t_1}, d_{t_2}) = \lambda_d \cdot s(t_1, t_2) \cdot \max(0, m_p - d_{t_1}^T d_{t_2}) + (1 - s(t_1, t_2)) \cdot \max(0, d_{t_1}^T d_{t_2} - m_n)\]$\lambda_d$ используется для исправления преобладания слагаемых для несвязанных тайлов.
Датасет
С сетью и тренировкой разобрались, осталось понять на чем тренировать. К сожалению, достаточно представительного датасета для данной задачи нет. Поэтому авторы генерируют синтетический датасет изображений с особыми точками. Синтетический датасет имеет массу плюсов. Его можно сделать достаточно большим не тратя ресурсы на “разметку”. Можно в него поместить примеры для всех классов особых точек, которые считаются полезными. Например, в данном случае в датасете особыми помечены точки на персечении двух или более линий, концы отрезков, углы “шахматной” раскраски и т.п:

Итак авторы нагенерировали синтетических изображений с особыми точками, затем расширили этот набор, применяя случайные преобразования гомографии с его элементам. На том что получилось авторы натренировали детектирующую часть сети, описанной выше и назвали её MagicPoint. Оказалось, что эта сеть демонстрирует отличные результаты на синтетических картинках существенно опережая классические FAST, Harris corners и GFTT (good features to track). Однако, на нормальных, а не синтетических изображениях, всё оказалось не так прекрасно и новый подход сильно проигрывал классике с точки зрения повторного распознавания точек после преобразования картинки. Поэтому авторы пришли к следующему способу получения датасета на реальных картинках.
Адаптация гомографии
Итак, у нас есть MagicPoint сетка, которая умеет детектировать особые точки на изображении, но не все и не очень хорошо. Теперь предположим у нас есть достаточно большой набор каких-то картинок, если просто разметить этот набор при помощи MagicPoint сети этого будет не достаточно. Поэтому авторы предлагают итеративный процесс основанный на утверждении, что особые точки изображения должны быть инвариантны относительно преобразования гомографии.
На каждой итерации мы улучшаем датасет. Берем изображение и несколько случайных преобразований гомографии. Объеденяем особые точки, которые MagicPoint найдет на исходном изображении и на изображениях полученных из исходного при помощи преобразований гомографии. Пройдя таким образом все изображения, получим новый вариант датасета, на котором перетренируем наш MagicPoint детектор и снова запустим поиск особых точек с расширением гомографией.
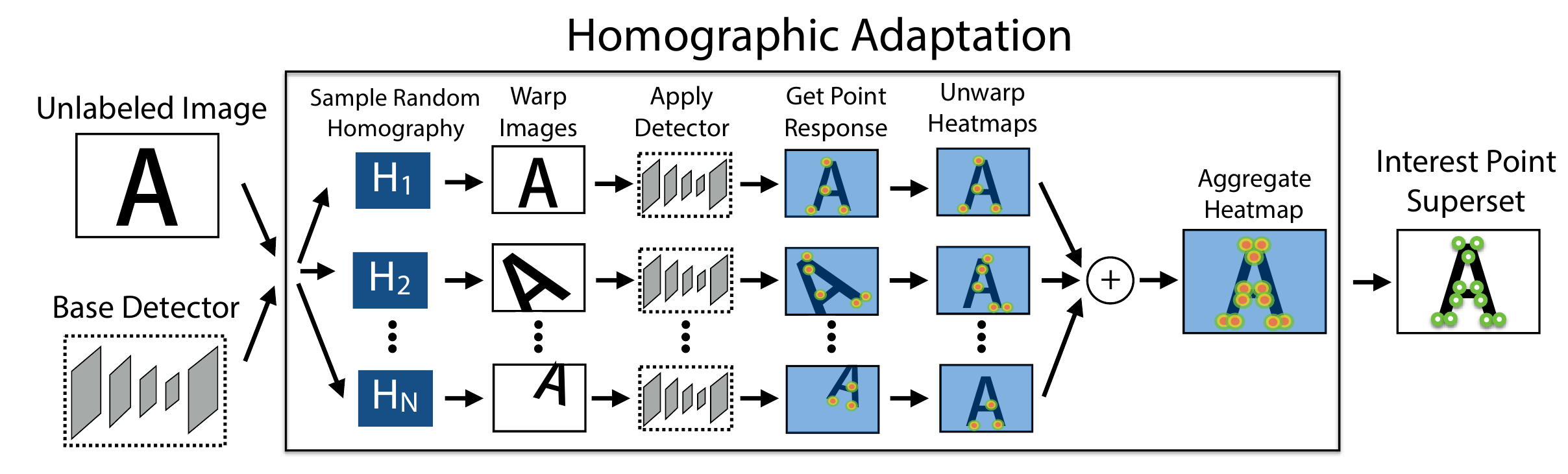
Количество преобразований гомографии для каждого изображения это гиперпараметр алгоритма, авторы пишут, что на MS-COCO минимально надо использовать 100 преобразований, чтобы получить хороший результат (repeatability score увеличивается на 21%). Авторы приводят картинки с детектированием точек на разных итерациях процесса:

После того как итеративную разметку датасета сочли достаточной, остаётся натренировать сеть, на обе ветки включая генерацию дескриптора.
Результаты
Авторы для тренировки использовали картинки из MS-COCO, а проверялись на датасете HPatches, сравнивая свой генератор особых точек с ORB, SIFT и LIFT. В оценке гомографии новый подход показал результаты даже лучще чем SIFT (остальные отстали еще сильнее), но лучшую повторяемость продемонстрировал ORB, правда у него специфические наборы особых точек, которые оказались не шибко хороши для восстановления параметров гомографии.
В целом идея в статье предложена интересная. Как минимум не требующая вкладывать ресурсы в разметку и при этом дающая возможность тренировать детектор на определенных изображениях т.е. можно затачивать детектор на специфичный домен, возможно это хорошо.