arXiv:2003.07064v2

То что свёрточные сети инвариантны к сдвигам картинки давно уже стало “общим местом” в работах по этому предмету. На самом деле, это крайне полезное свойство при классификации объекта на фотографии, где бы не был “котик” в левом или правом верхнем углу это не должно влиять на ответ классификатора. Если объект сдвигается на фотографии, то соответствующим образом сдвигаются и “ответы” свёрточных слоёв, а после всех свёрточных слоёв сейчас обычно принято ставить какой-то глобальный пулинг (либо усреднение, либо максимум), который тоже инвариантен к сдвигам.

Однако, есть одна тонкость, с которой авторы статьи решили разобраться, а именно поведение свёрточных слоёв на краях картинки.

Рассмотрим следующую задачу. Допустим мы берем изображение одного и того же объекта и размещаем его в верхнем левом (класс 1) или в правом нижнем (класс 2) углу изображения:

Если свёрточная сеть полностью инвариантна к сдвигу, то она не сможет различить такие два класса. Однако, авторам удалось натренировать простую сеть состоящую из одного свёрточного слоя и глобального пулинга, которая отлично сумела классифицировать положение объекта. А значит свёрточная сеть использует абсолютную позицию объекта, хотя вроде бы не должна этого уметь. Авторы предположили, что это связано с использованием сетью краевых эффектов. Действительно, на краю картинки свёртка вынуждена работать с отсутствующими данными. Это даёт возможность натренировать такие фильтры, которые будут выдавать ответ только, например, для объектов в верхней части изображения. Понятно, что эффект зависит от размера свёрточного фильтра, но поскольку обычно свёрточная сеть состоит из целого стека свёрток, то исходное поле откуда берутся данные для одного отзывая на вершине пирамиды становится достаточно большим.

Кодирование позиции при помощи граничного эффекта

Итак гипотезы заключается в том, что за счёт граничного эффекта, свёрточная сеть может натренировываться на различение позиций объектов.

Допустим мы будем обрабатывать при помощи свёрточного слоя тензор размерности $d$, причем для простоты будем смотреть на одномерный случай ($d=1$). Пусть $x \in \mathbb{R}^n$ одномерное одноканальное изображение (сигнал) длины $n$ и $f \in \mathbb{R}^{2k+1}$ одномерный одноканальный фильтр (нечётная длина $2k+1$ взята просто для удобства, можно и чётной длины фильтр рассматривать). Выход свёртки будет иметь вид:

Для некоторых $t$ и $j$, возможна ситуация когда $t-j < 0$ (или $t-j \ge n$), и следовательно значение $x_{t-j}$ выходит за границы изображения. Для разрешения таких ситуаций изображение дополняется (padding) за своими границами. Авторы статьи рассматривают два варианта дополнения изображения: а) дополнение нулями (zero padding) и б) цикличное дополнение (circular padding) - в этом случае при необходимости получить значения за границей изображения, берутся значения с другой стороны, т.е. происходит как бы “зацикливание” картинки.

Авторы рассматривают три типа свёртки:

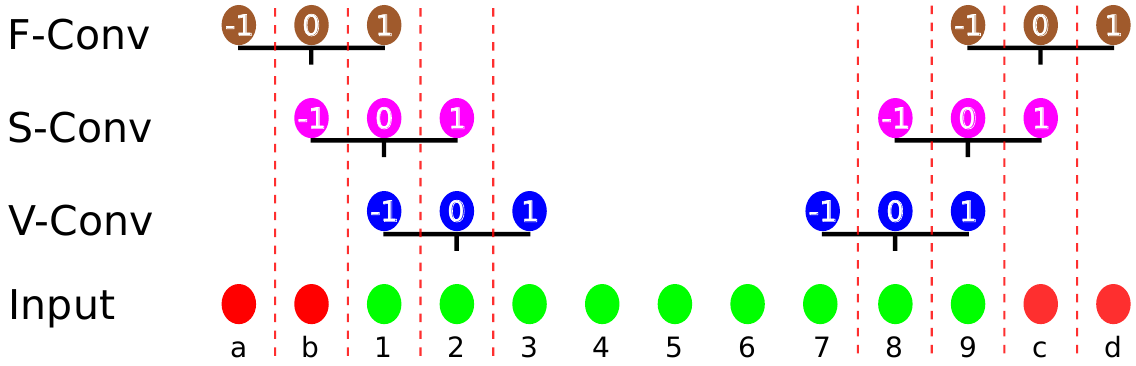
1. Допустимая свёртка (valid convolution, V-Conv) - в этом случае свёртка не “заглядывает” за границы изображения. Т.е. берётся $t \in [k+1, n-k]$, а значит мы сворачиваем сигнал длины $n$ в сигнал длины $n - 2k$, срезая по $k$ элементов с каждой стороны изображения. Этот вариант свёртки не требует дополнения изображения, используя только имеющиеся значения сигнала.

2. Сохраняющая размер свёртка (same convolution, S-Conv) - здесь центр свёрточного фильтра пробегает по все элементам сигнала. При этом возникает необходимость дополнять изображение за его границами (по $k$ элементов с каждой стороны). Размер изображения после данного типа свёртки не уменьшается и $t \in [1, n]$

3. Полная свёртка (full convolution, F-Conv) - каждый элемент свёрточного ядра применяется к каждому элементу изображения. При этом $t \in [-k, n+k]$ и с каждой стороны изображение увеличивается на $k$. Естественно, в данном случае тоже необходимо будет дополнять изображение за его границами, добавляя бордюр ширины $2k$.

Насколько одинаково эти три типа свёртки используют исходные данные? Чтобы это узнать авторы подсчитывают какое количество раз значение сигнала на позиции $a$ в векторе $x$ используется при применении свёрточного преобразования:

здесь $\delta_{i,a-j}$ - символ Кронекера.

Замечание. С моей точки зрение, понятнее было бы записать $С(a) = \sum_t \sum_{j=-k}^{k} \delta_{a,t - j}$. Т.е. суммируем по всем возможным выходным откликам $t$, и каждый раз во внутренней сумме добавляем единичку, если дергаем значение вектора ($x_{t - j}$) с позиции $a$. Результат при этом бы никак не изменился

В отсутствии граничных эффектов $C(a) = 2k + 1$ для всех $a$.

Теперь разберем три типа свёрток, которые описаны выше.

1. V-Conv. Как уже было сказано в этом случае мы берём $t \in [k+1, n-k]$ и значит:

   \[C_V(a) = \sum_{i=k+1}^{n-k} \sum_{j=-k}^{k} \delta_{i,a-j}= \begin{cases} a, & a \in [1, 2k]\\ n - a + 1, & a \in [n - 2k, n]\\ 2k + 1, & a \in [2k+1, n-2k-1] \end{cases}\]

   Т.е. очевидно, что в случае V-Conv есть некоторые позиции на изображении к которым применяются не все веса фильтра.

2. S-Conv. Аналогично ограничиваем суммирование:

   \[C_S(a) = \sum_{i=1}^{n} \sum_{j=-k}^{k} \delta_{i,a-j}= \begin{cases} a + k, & a \in [1, k]\\ n - a + k + 1, & a \in [n - k, n]\\ 2k + 1, & a \in [k+1, n-k-1] \end{cases}\]

   И снова, как и в предыдущем случае, найдуться такие позиции на изображении к которым фильтр не применяется полностью.

   Однако, если в случае S-Conv использовать цикличное дополнение (circular padding) изображения, то не смотря на то, что полученная только что формула останется справедливой для абсолютной позиции $a$, мы сделаем одинаковым количество использования именно значений $x_a$ исходного вектора в этой позиции за счет “выдёргивания” значений близких к правой границе для дополнения отсутствующих значений за левой границей.

3. F-Conv

   \[C_А(a) = \sum_{i=1}^{n} \sum_{j=-k}^{k} \delta_{i,a-j} = 2k+1\]

   В данном случае результат аналогичен тому, который получается в отсутствии граничных эффектов.

Таким образом, авторы предполагают, что наиболее чувствительным к граничным эффектам и, следовательно, лучше всех использующим абсолютную позицию будет V-Conv. S-Conv с дополнением изображения нулями так же будет чувствителен к граничным эффектам, хотя и не так сильно как V-Conv. В случае же, же если изображение дополняется циклически, то на S-Conv не должны влиять граничные эффекты, однако, дополнение такого типа может привести к другого рода “шумам”. И, наконец, F-Conv - должен быть инвариантен к граничным эффектам. В качестве иллюстрации авторы приводят следующую схему:

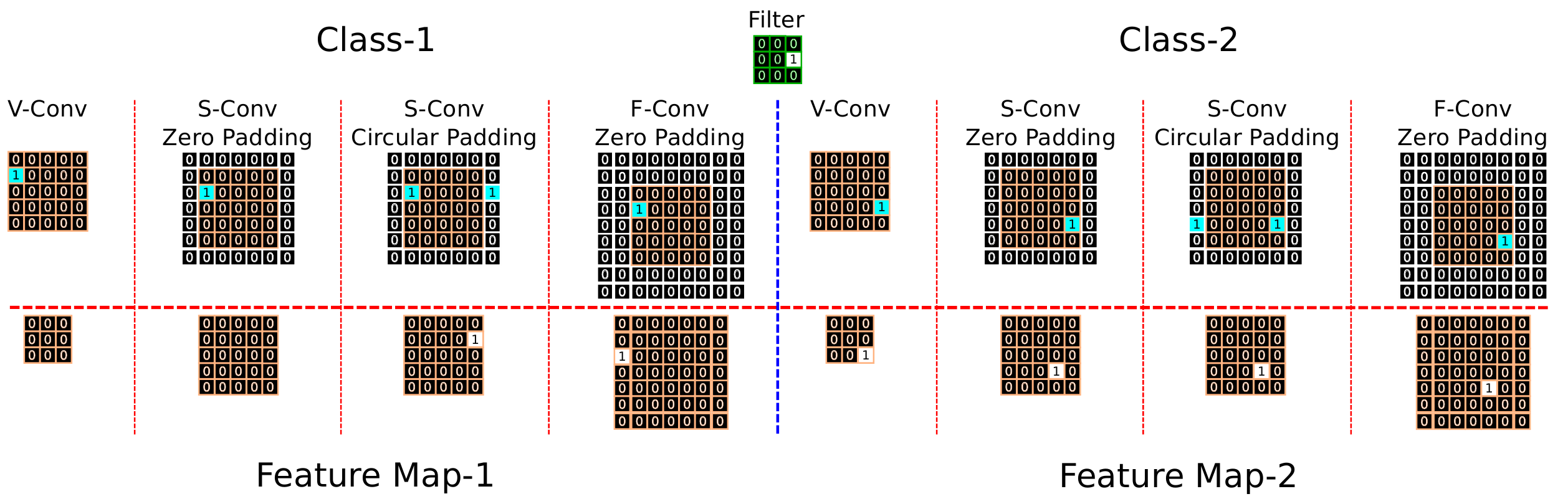
Эксперименты

Высказав теоретическое обоснование, авторы решают проверить свою теорию практикой.

Замечания. F-Conv не является стандартным свёрточным фильтром, однако, его легко реализовать используя стандартную свёртку и увеличив ширину добавляемого к изображению бордюра. В случае разностных сетей, выход с разностного слоя также расширяется бордюром с нулями, чтобы добиться совпадения размеров.

Насколько далеко от границы может действовать граничный эффект?

Первый эксперимент который проводят авторы, должен проверить насколько далеко от границы изображения продолжает действовать граничный эффект. Для этого выбрали 3’000 картинок из ImageNet, отмасштабировали их к $56 \times 56$ и разбили на три равные части (тренировочную, валидационную и тестовую). Далее взяли черную размером $112 \times 112$ картинку и для генерации первого класса помещали изображение $56 \times 56$ в левый верхний, а для изображений второго класса в правый нижний угол. Теперь чтобы ответить на вопрос параграфа сделали из этого набора изображений $112 \times 112$ (по 2’000 для тренировки, валидации и тестов) 7 наборов (добавив 6 новых), обведя картинки черным кантом шириной: $\{0, 16, 32, 64, 128, 256, 512\}$

Авторы пробовали три сети:

1. BagNet-33 - это ResNet с ограничением до $33 \times 33$ поля на исходном избражении, которое сворачивается в один пиксель карты откликов

2. ResNet-18 - как свёрточную сеть средних размеров

3. DenseNet-121 - достаточно большая сетка.

Каждая сеть тренировалась в трёх вариантах:

a. полностью с нуля

b. инициализированна случайными весами, затем веса свёрток заморожены.

с. свёрточные веса претренированы на ImageNet и затем заморожены.

Результаты можно посмотреть на графиках:

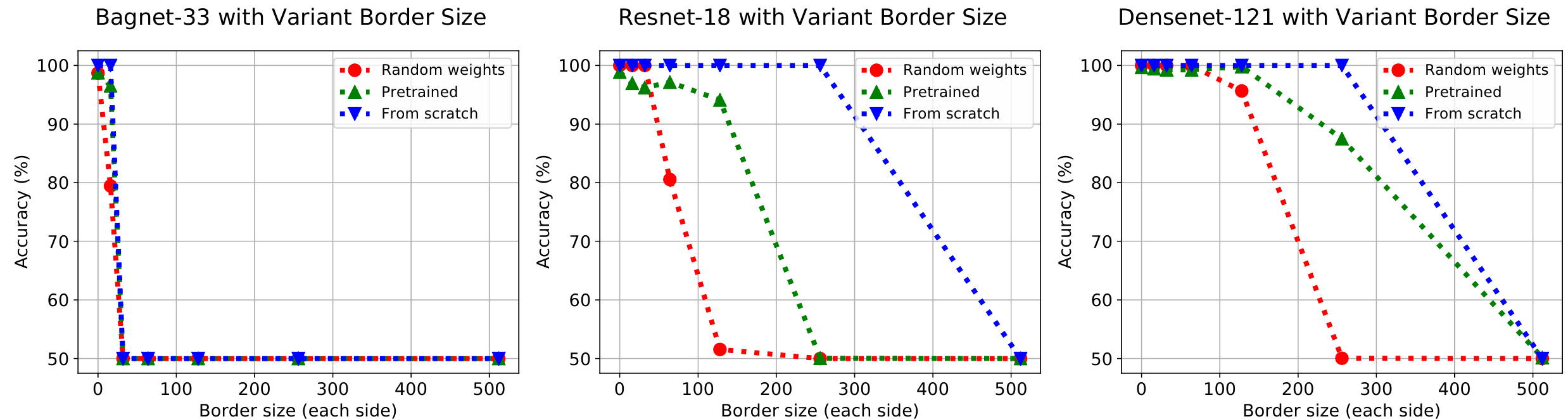
Видно, что все три сети смогли классифицировать позицию при любом из трёх вариантов тренировки. Хуже всего дело, очевидно, обстоит для случайных весов, в том смысле, что они могут классифицировать по позиции только когда объект достаточно близко к границе. В случае когда веса претренированы на ImageNet, то сети удаётся классифицировать по позиции даже в случаях когда объект существенно дальше от границы, чем в случае случайных весов. Откуда авторы статьи делают вывод, что среди фильтров претренированных на ImageNet есть некоторое количество, которые используют информацию о позиции объекта для классификации объектов на фотографии (т.е. решения исходной задачи классификации ImageNet, а не той модельной которую рассматривается в статье). Наконец, сеть тренированная “from scratch” показывает наилучший результат, и классифицирует позицию для объектов на еще более существенном удалении от края изображения.

Если говорить о структуре сети, то видно, что BagNet, даже тренирумая с нуля, не может классифицировать по положению далеко от границы картинки. ResNet-18, с весами претренированными на ImageNet, может классифицировать позицию на расстоянии 128 пикселей от границы, при этом ImageNet работает c картинками размера $224 \times 224$ и значит максимальное расстояние до границы не превышает 112 пикселей.

Как работает граничный эффект на разных типах свёртки?

Предыдущий эксперимент показал, что граничный эффект действительно есть, и в том числе даже сеть натренированная для классификации объектов (не положения) на ImageNet тоже содержит свёртки, которые работают, используя позицию объекта.

Теперь авторы хотят выбрать такой вариант свёрточных фильтров, которые не были бы подвержены граничному эффекту. Рассматриваются те три типа свёрток, которые были описаны ранее (V-Conv, S-Conv, F-Conv). Предлагается следующий эксперимент: будут рассматриваться черные изображения размера $32 \times 32$ с двумя квадратами размера $4 \times 4$ один квадрат зеленый, второй красный. Сетка должна научиться разделять такие изображения на два класса: первый класс, когда зеленый квадрат справа, а красный слева, и второй класс, наоборот, зеленый - слева, красный - справа. Такая задача классификации, очевидно никак не привязана к абсолютной позиции. Однако, авторы в качестве тренировочного датасета генерируют изображения в которых для первого класса цветные квадраты расположены ближе к верхнему краю изображения (средний отступ от верхнего края 8 пикселей), а для второго класса цветные квадраты смещены к нижнему краю избражения (средний отступ от нижнего края 8 пикселей), таким образом смещая выборку по абсолютной позиции. Если свёртки действительно инвариантны к позиции объекта на изображении, то это не должно повлиять на результат. Для проверки генерируются два набора: первый с таким же смещением абсолютных позиций как и тренировочный, и второй, в котором смещение изменено, т.е. для первого класса квадраты ближе к нижнему краю, а для второго к верхнему.

Для классификации авторы тренировали сеть из четырёх свёрточных слоёв, первые два слоя содержать 32 фильтра, вторые два слоя - 64 фильтра, и в конце слой пулинга максимального элемента. В качестве, свёрток использовались три типа, описанные выше. Результаты проверки на двух тестовых датасетах представлены в таблице:

Type     | Pad  |  Similar test | Dissimilar test |
---------------------------------------------------
V-Conv   |  -   |        100.0% |            0.2$ |
S-Conv   | Zero |         99.8% |            8.4% |
S-Conv   | Circ |         73.7% |           73.7% |
F-Conv   | Zero |         89.7% |           89.7% |

Видно, что первые два варианта (V-Conv и S-Conv с дополнением нулями) натренировались на абсолютную позицию, поскольку, показав отличные результаты на тестовом наборе с тем же смещение выборки по абсолютной позиции, что и тренировочный, на наборе с обратным смещением не смогли решить задачу классификации совсем. Для случаем S-Conv c циклическим дополнением и F-Conv качество уже не зависило от тестового набора, но видно, что за счет артефактов, которые появляются при циклическом дополнении, качество с S-Conv хуже чем с F-Conv.

Далее авторы приводят еще три эксперимента, которые я не буду подробно разбирать. Останавлюсь только на части одного из них.

Влияние размера датасета

Авторы тренировали ResNet-50 на ImageNet с разными вариантами свёрток (S-Conv и F-Conv). Для каждого типа свёртки тренировалось пять вариантов сети: выбирая 50, 100, 250, 500 и все изображения для каждого класса представленного в ImageNet. Меряли точность полученных сетей. График выглядит следующим образом:

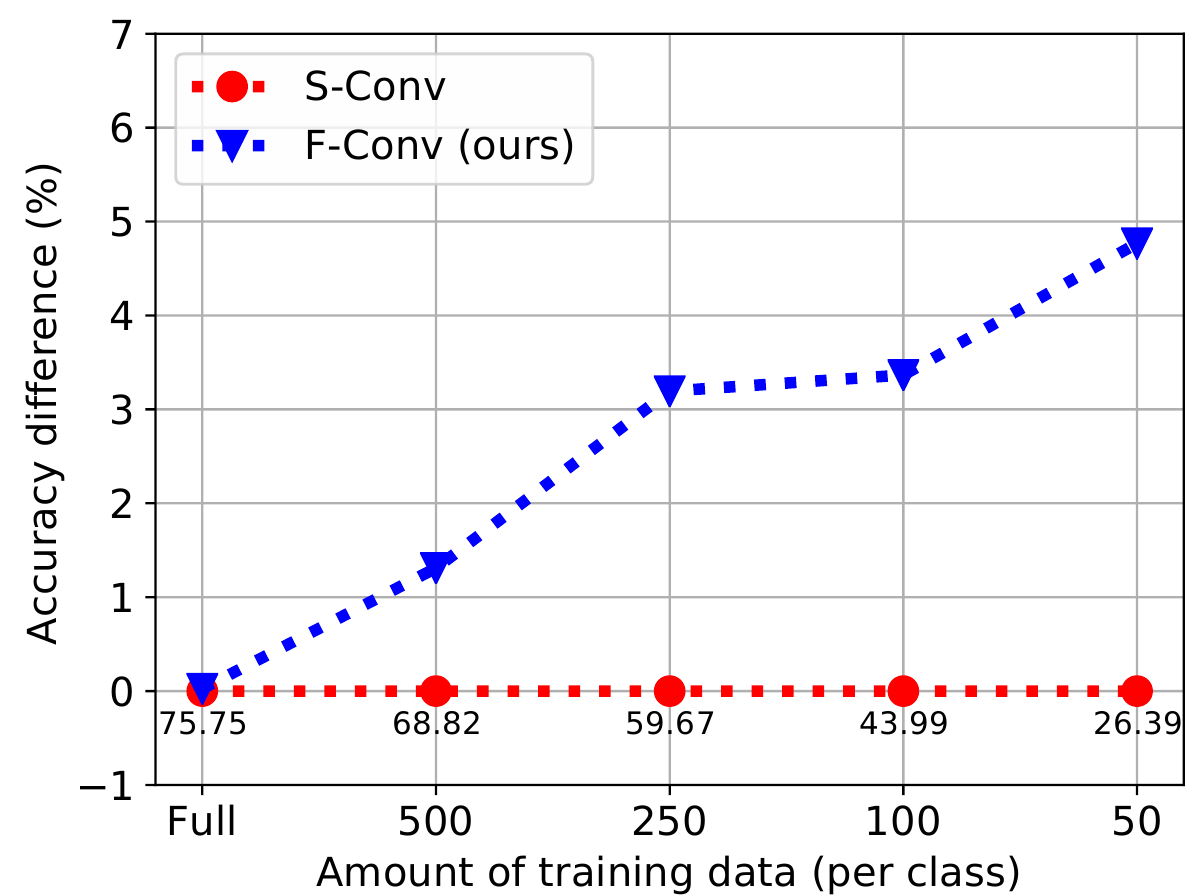
Видно, что при уменьшении размера датасета, вариант с F-Conv справляется лучше. На датасете из 50 элементов вариант с S-Conv выдаёт точность 26.4%, а F-Conv - 31.1%, это относительный прирост 17.8%. Правда надо отметить, что на всём датасете изменения качества нет совсем, а и 26% и 31% качество крайне низкое.