arXiv:1410.5401

Что такое машина Тьюринга все, наверное, знают. В статье рассказывается о некоем аналоге такой машины на базе нейронных сетей.

Т.е. разбирается вопрос можно ли обучить сеть выполнять какой-нибудь алгоритм, используя подход “обучения с учителем”, т.е. на базе набора примеров. Не просто классифицировать или даже генерировать картинку-текст-видео, а именно, чтобы сама сеть “написала” программу по набору примеров, а потом на новых примерах её выполнила. Например, научилась копировать последовательность данных или сортировать их и т.п.

Известен результат, что рекуррентная нейронная сеть (RNN) может представлять универсальную машину Тьюринга (см. здесь ), проблема только в том, что теоретически то она может, но практически имеются некоторые проблемы, чтобы получить нужный результат.

Авторы предлагают добавить к нейронной сети достаточно большой блок постоянной памяти, по аналогии с бесконечной лентой машины Тьюринга, важно, чтобы получившаяся конфигурация оставалась дифференцируемой, тогда мы будем иметь возможность обучать машину нужной программе, используя известные градиентные методы.

Предлагается следующая схема:

На каждом шаге, контролер (это некая нейронная сеть, либо обычная, либо рекуррентная (LSTM)), получает на вход данные из внешней среды, обрабатывает их и отдаёт что-то на выход. Вход и выход контролера как и любой нейронной сети это множество векторов. При этом имеется дополнительная память, с которой контролер общается через множество головок - по аналогии с лентой в машине Тьюринга. Есть читающие головки, которые извлекают, данные из внутренней памяти и пишущие головки, которые данные в этой памяти меняют.

Важно, что все действия проводимые машиной дифференцируемы, иначе ни о каком обучении градиентным спуском речи уже не будет. Чтобы не потерять дифференцируемость авторы используют такие операции чтения и записи, которые в большей или меньшей степени задевают все элементы памяти, в отличии от машины Тьюринга, которая работает с конкретным элементом. Чтение и запись получаются “размытыми”. Как это выглядит мы сейчас разберёмся.

Память

Память представляет из себя набор из $N$ векторов каждый длины $M$

Чтение

Чтобы прочитать из памяти на шаге $t$ вектор $R^{(t)}$ длины $M$ необходимо, сгенерировать набор весов $W^{(t)} = (w_0^{(t)}, …, w_{M-1}^{(t)})$, т.ч.

\[\sum_i w_{i}^{(t)} = 1, \;\; 0 \le w_{i}^{(t)} \le 1, \;\; \forall i\]

тогда, результат получается как выпуклая комбинация векторов $D_i^{(t)}$ из памяти:

\[R^{(t)} = \sum_i w_{i}^{(t)}D_i^{(t)}\]

Уточним два обстоятельства, во-первых, такой подход дифференцируем относительно и данных в памяти и весов. Во-вторых, отметим, что может быть несколько “читающих головок”, каждая при этом сгенерирует свой набор весов для чтения.

Запись

Запись состоит из двух частей: вначале стирание и затем добавление.

Каждая пишущая головка, как и читающая генерирует вектор весов $W^{(t)}$, который является, в определенном смысле адресом области в памяти с которой предполагается работа. Кроме того, пишущая головка генерирует еще два вектора: стирающий вектор $E^{(t)}$ и вектор добавлений $A^{(t)}$. Эти два вектора так же оба длины $M$, и компоненты стирающего вектора лежат внутри отрезка $(0, 1)$.

Итак, каждая пишущая головка последовательно осуществляет две операции. Первая - стирание:

\[\tilde{D}_i^{(t)} = D_i^{(t-1)}\odot(\mathbf{1} - w_{i}^{(t)} E^{(t)})\]

здесь $\odot$ - поэлементное умножение, а $\mathbf{1}$ - вектор строка из единиц. Получается, что мы сотрём те элементы в памяти, для которых одновременно равны единице и вес $w_{i}^{(t)}$ (отвечающий за адресацию) и компонент стирающего вектора.

Вторая операция - добавление:

\[D_i^{(t)} = \tilde{D}_i^{(t)} + w_{i}^{(t)} A^{(t)}\]

Эта операция меняет элемент в памяти адресованный вектором весов $W^{(t)}$.

Обе операции дифференцируемы, а значит и их композиция тоже, так же дифференцируемой остаётся и случай, когда применяется несколько пишущих головок.

Механизм адресации

Операции чтения и записи требуют вектор весов, который в определенном смысле осуществляет адресацию данных в памяти. Авторы выделяют два механизма адресации: первый адресация по содержимому, второй адресация по позиции.

Адресация по содержимому предполагает, что контролер выдаст “запрос” - какой-то вектор, а потом сравнивая этот “запрос” с данными в памяти можно будет выбрать наиболее близкое значение и соответственно определить адрес в памяти с которым собираемся работать. Однако, такой способ подходит не для всех задач, иногда полезно уметь обращаться к данным, расположенным в конкретном месте в памяти. Механизм адресации в нейронной машине Тьюринга (НМТ) объединяет эти два случая.

В качестве входных данных для получения нового весового вектора $W^{(t)}$ у нас есть во-первых, вектор весов с предыдущего шага $W^{(t-1)}$, и во-вторых, данные расположенные в памяти $D^{(t)}$. Контролер генерирует пять величин: $K^{(t)}$, $\beta^{(t)}$, $g^{(t)}$, $S^{(t)}$ и $\gamma^{(t)}$, отвечающих за адресацию

Адресация по содержимому

Возьмем вектор ключ $K^{(t)}$ и вектор силы ключа $\beta^{(t)}$ и сгенерируем промежуточный вектор $C^{(t)}$, который зависит от схожести элемента в памяти и вектора ключа:

\[C_i^{(t)} = \frac {\exp \left(\beta^{(t)} \mu\left(K^{(t)}, D_i^{(t)}\right) \right)} {\sum_{j} \exp \left(\beta^{(t)} \mu\left(K^{(t)}, D_j^{(t)}\right) \right)}\]

здесь $\mu(\cdot, \cdot)$ - мера схожести двух векторов. Авторы используются для этого косинус-метрику:

\[\mu(U, V) = \frac {U \cdot V} {\left \| U \right \| \left \| V \right \|}\]

Адресация по позиции

Механизм адресации по позиции сделан таким образом, чтобы его одновременно можно было использовать и для простого итерирования по памяти, и для произвольного доступа. Это реализуется при помощи кругового сдвига весов. Например, если у нас есть набор весов, который сфокусирован на некоторой позиции в памяти, то мы можем сдвинуть его на 1 и переместить фокус на следующую позицию.

Прежде чем приступить к сдвигам, смешаем веса с предыдущего по времени шага $W^{(t-1)}$ и веса, полученные процедурой адресации по содержимому, $C_i^{(t)}$ при помощи интерполяционных ворот - скаляра $g^{(t)} \in (0, 1)$:

\[\hat{W}^{(t)} = g^{(t)} C^{(t)} + (1 - g^{(t)}) W^{(t-1)}\]

После интерполяции, делаем сдвиг весов. Для этого используется вектор $S^{(t)}$ (нормализованное распределение на наборе допустимых целочисленных сдвигов) с которым мы сворачиваем веса $\hat{W}^{(t)}$:

\[\tilde{W}_i^{(t)} = \sum_{j=0}^{N-1} \hat{W}_j^{(t)} S_{i-j}^{(t)}\]

здесь арифметические операции с индексами весовых коэффициентов делаются по модулю $N$. Проблема однако состоит в том, что при таком преобразовании сдвига, если вес был сосредоточен в некоторой позиции, то он “размажется”. Действительно, допустим мы выбрали три сдвига: $-1$, $0$, $1$, и задали, им соответствующие веса $0.1$, $0.8$, $0.1$, после “сдвига”, вес сосредоточенный в одной точке размажется между тремя, чтобы побороть эту проблему окончательно веса получаются при помощи дополнительной фокусировки с использованием скаляра $\gamma^{(t)}$:

\[W_i^{(t)} = \frac {\left(\hat{W}_i^{(t)}\right)^{\gamma^{(t)}}} {\sum_{j} \left(\hat{W}_j^{(t)}\right)^{\gamma^{(t)}}}\]

Контролер

В качестве контролера авторы предлагают два варианта сетей: обычная сеть с прямой связью, и рекуррентная нейронная сеть на базе LSTM ячеек. Обычная сеть более понятна, и её шаблоны записи и чтения памяти проще интерпретировать, зато LSTM сеть кроме “внешней” памяти имеет еще и “внутреннюю” это делает ситуацию похожей на работу обычного CPU, который может обращаться к памяти и при этом имеет еще и внутренние регистры.

Эксперименты

Авторы экспериментируют с возможностью сети научиться решать несколько простых алгоритмических задач, при этом важно чтобы сеть сумела обобщить решение. Например, если сеть обучается решать задачу копирования последовательности, и при этом в качестве примеров ей предоставлены последовательности длины до 20 элементов, то хочется чтобы сеть обобщила решение задачи и научилась копировать последовательности длины 100 и т.д.

Все эксперименты проводятся для трёх архитектур: НМТ с контролером в виде обычной сети с прямой связью, НМТ с контролером в виде рекуррентной сети из LSTM ячеек, и наконец, обычная рекуррентная сеть из LSTM ячеек.

Копирование

Первый эксперимент копирование последовательности. Сеть тренируется копировать последовательность восьмибитовых случайных векторов. При обучении длина последовательности выбирается случайной от 1 до 20, для обозначения конца последовательности на вход подаётся разделительный флаг. На выходе сеть должна выдать копию входной последовательности (без разделительного флага).

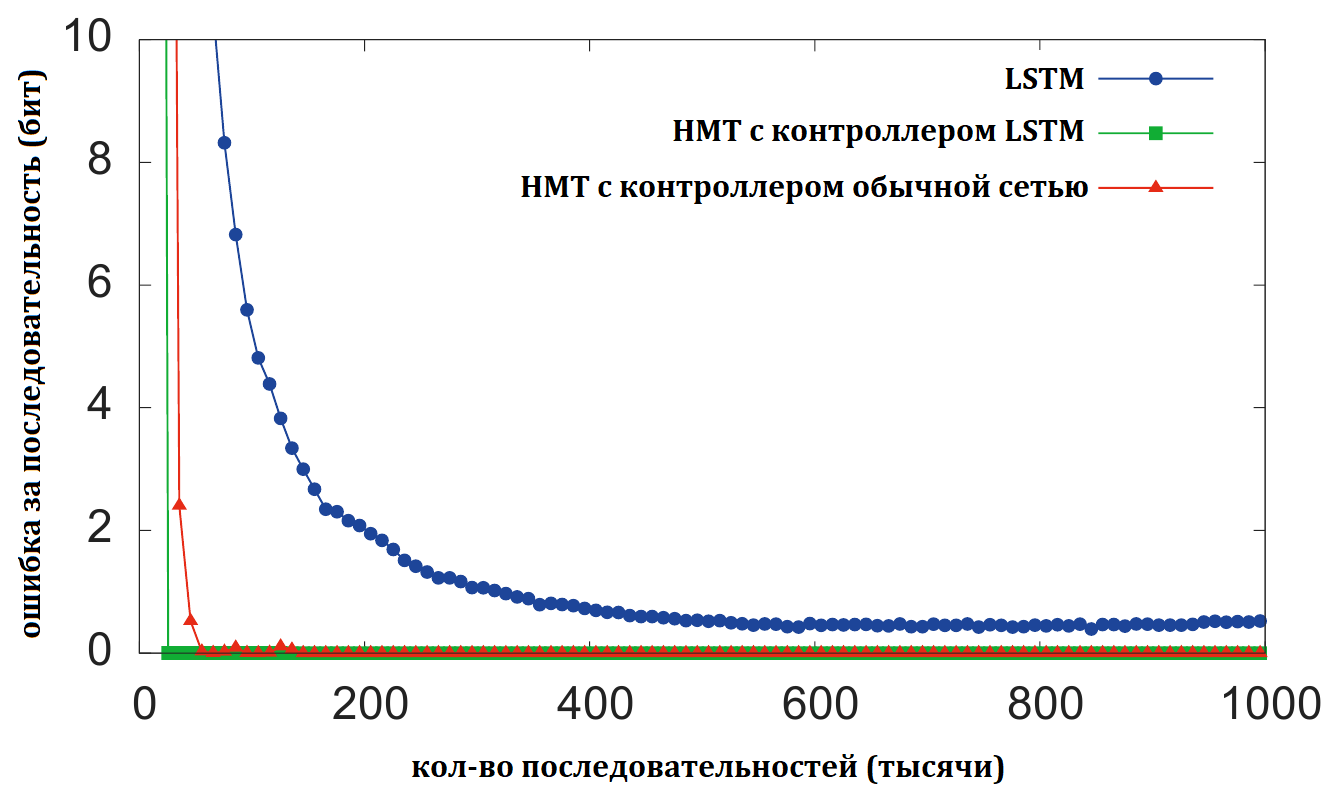
На графике видно, что в случае НМТ (и с обычной сетью в качестве контролера, и с LSTM) тренровка сходится достаточно быстро, а просто рекуррентная сеть с LSTM ячейками даже после длительной тренировки не может достичь такого же уровня точности. С обобщением на более длинные последовательности НМТ так же показывает значительно лучший результат.

На рисунке представлен результат копирования НМТ, для случаев последовательностей длины 10, 20, 30, 50 и 120.

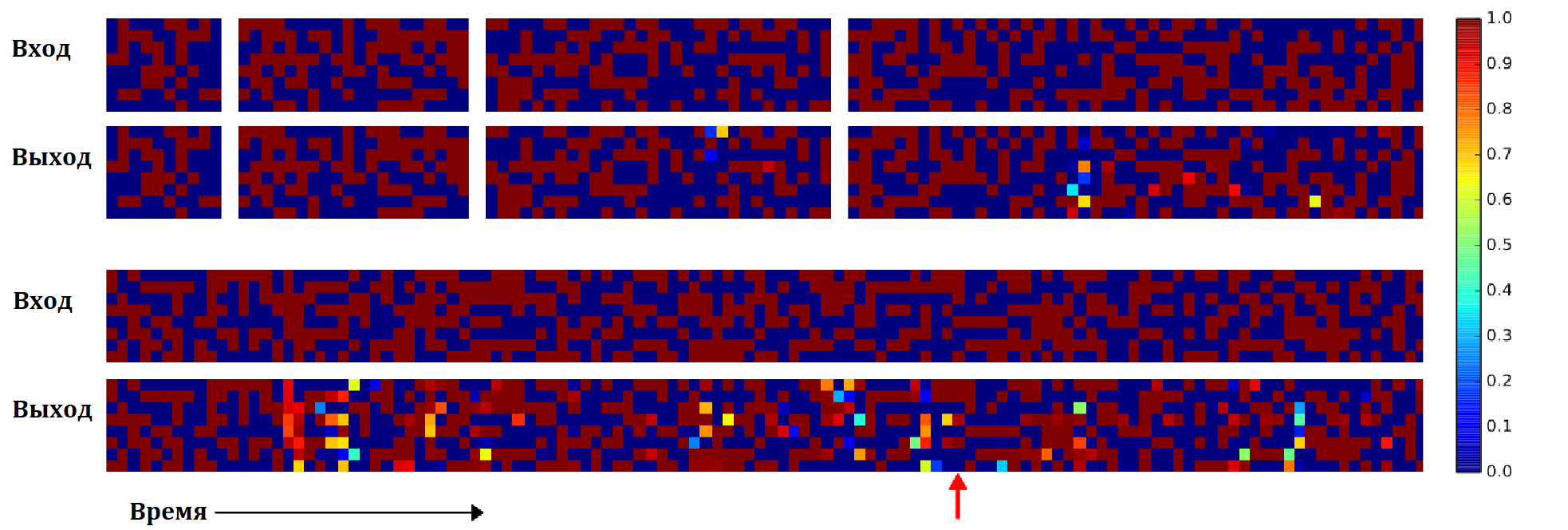
Видно, что последовательности длиной 10 и 20 копируются точно, для большей длины появляются ошибки, но незначительные. Только на последовательности длины 120 качество существенно проседает причем кроме локальных ошибок, возникает одна глобальная (отмечена красной стрелкой), один из векторов последовательности копируется дважды, после чего остальные вектора оказываются сдвинуты.

На следующем рисунке результат работы обычной LSTM сети.

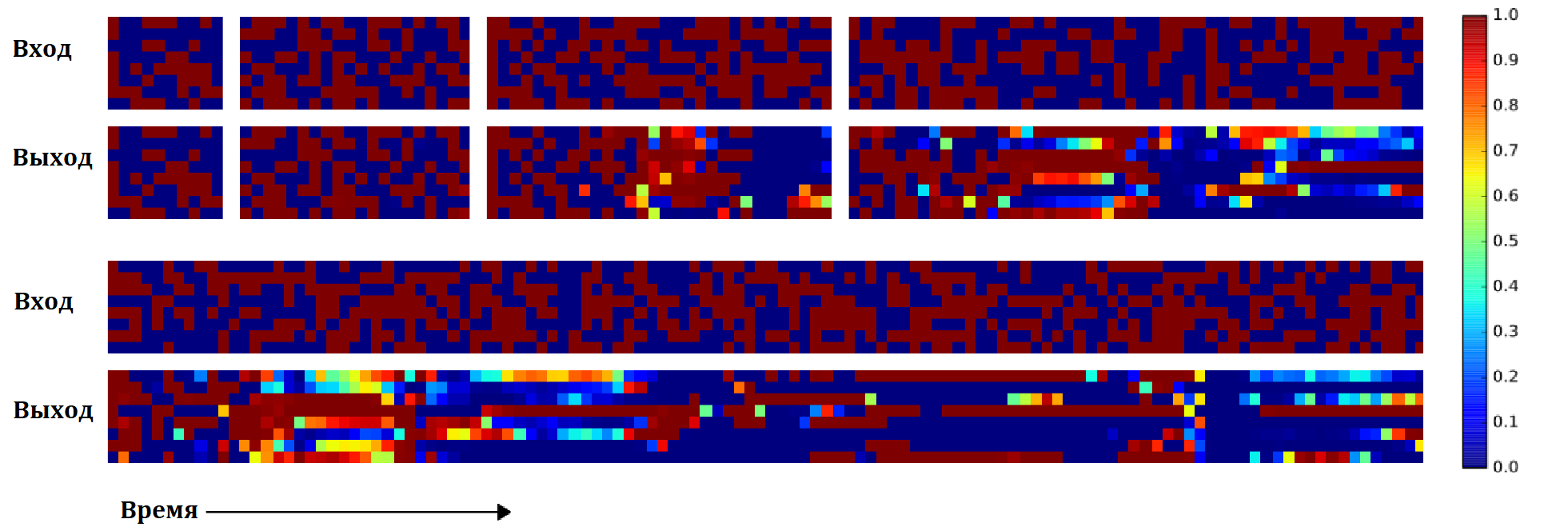
Видно, что данный вариант плохо обобщается на последовательности длины большей чем 20. При этом надо отметить, что с увеличением длины копируемой последовательности, длина правильно скопированного начала уменьшается.

Авторы проанализировали работу НМТ сети и предполагают, что сеть “научилась” следующему алгоритму копирования:

На следующей картинке изображено использование НМТ памяти при операции копирования:

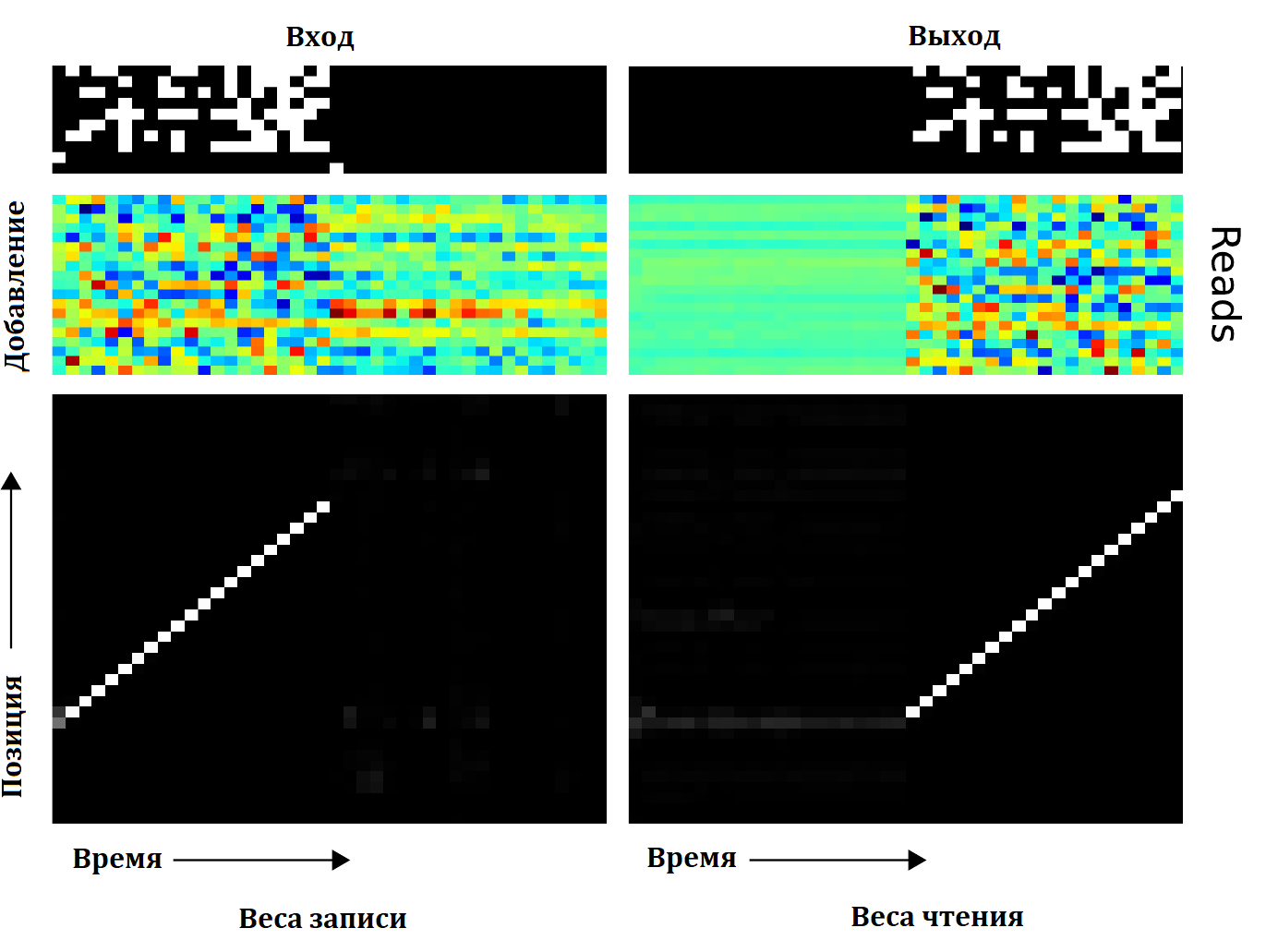
В левой колонке сверху вниз идут: входные вектора, вектора добавляемые в память и наконец, соотвествущие веса адресующие ячейки памяти (черный - ноль, белый - единица). В правой колонке идут: выходные вектора, вектора считываемые из памяти и веса адресации чтения. Видно, что фокус адресных весов ярко выражен и практически сеть на каждом шаге работает только с одной позицией в памяти. Так же виден сдвиг позиции на каждом шаге и, наконец, что позиция чтения в точности совпадает с позицией записи, а считываемые вектора совпадают с теми которые были добавлены. Отсюда и делается вывод о том алгоритме которому научилась сеть, на первой фазе, каждый входной вектор записывается в определенную позицию в памяти, а на второй также последовательно вектора из этих позиций вычитываются.

Авторы делают вывод, что сеть таким образом научилась создавать массив и итерироваться по его элементам.

Повторяющиеся копирование

Следующая задача используемая в экспериментах - повторяющиеся копирование. Т.е. входная последовательность, должна быть скопирована определенное число раз. Основная цель эксперимента проверить сможет ли НМТ научиться выполнять вложенную функцию. Идеально было бы получить возможность запускать цикл “for” внутри которого содержалось бы уже изученная функция.

В данном случае на вход подаётся последовательность случайной длины, состоящая из случайных векторов, а в завершении число, которое задаёт количество копий. Для тренировки длина последовательности и количество копий выбираются случайно от 1 до 10. На выход сеть должна вывести, соответствующие количество копий поданой последовательности и затем маркер окончания работы. Чтобы выдать маркер окончания работы, сеть должна во-первых, научиться отделять последнее число поданное на вход от чисел последовательности, а во-вторых, считать количество уже отданных копий.

График тренировки трёх рассматриваемых архитектур:

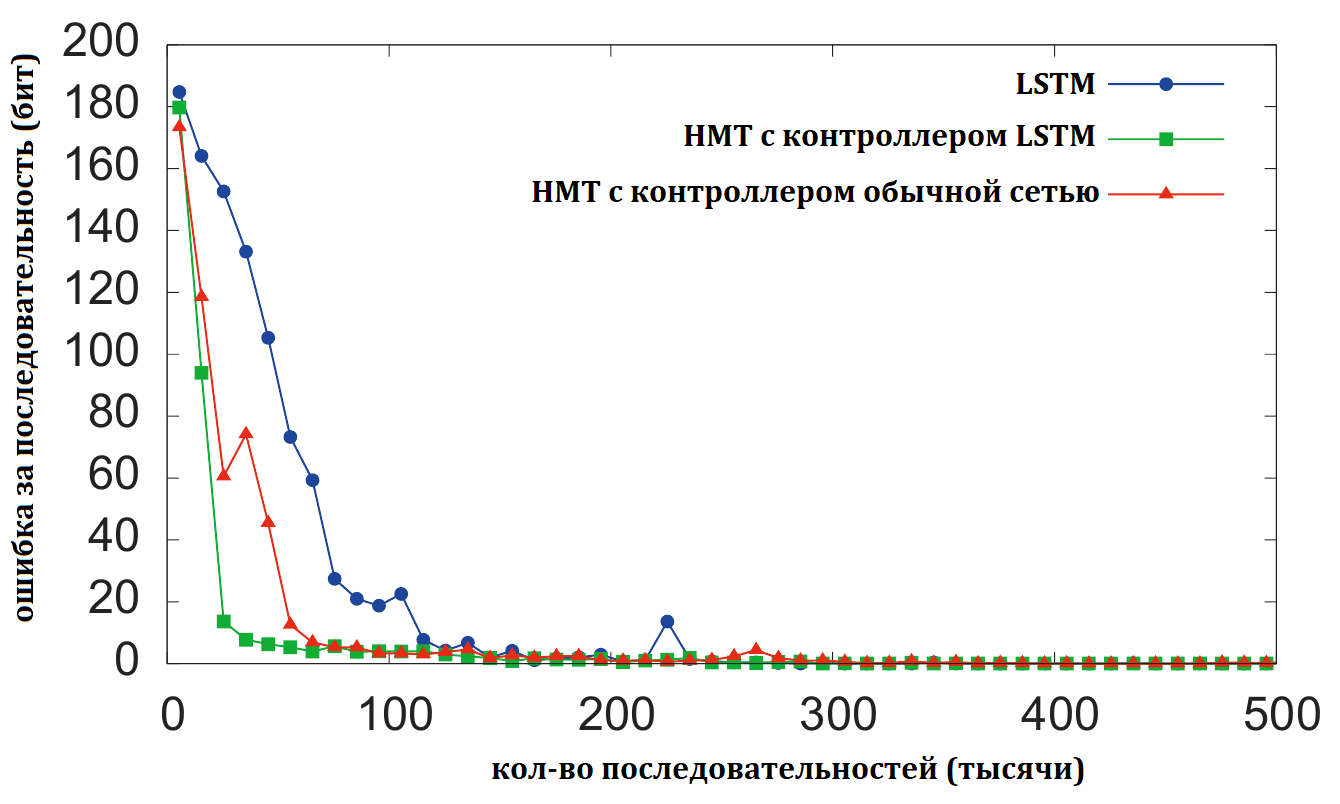
Как не странно в данном случае все три архитектуру втренировываются, в том числе и обычная рекуррентная LSTM сеть. Однако, различие между НМТ и простой LSTM сетью проявляется в генерализации.

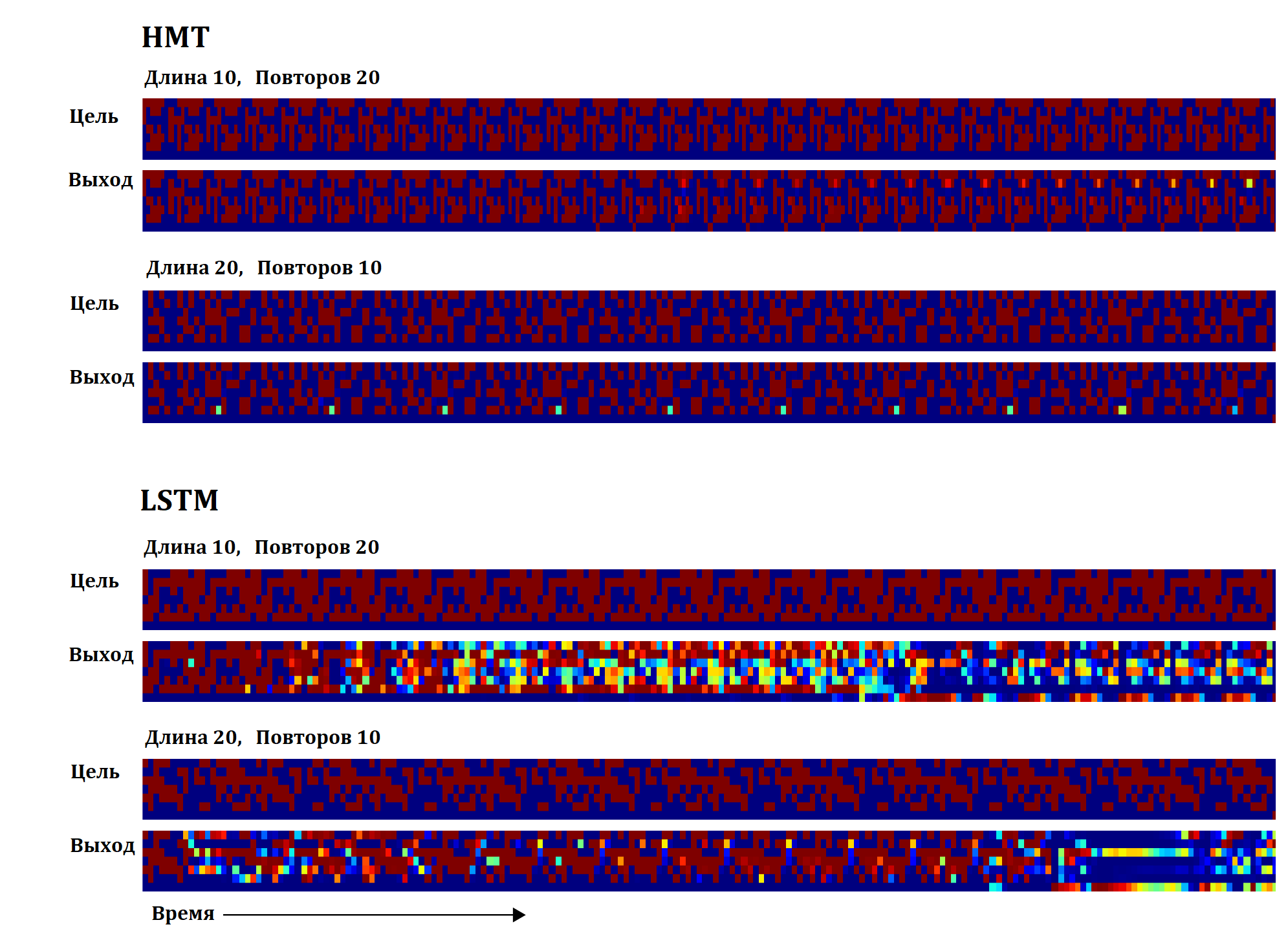
В данном случае, мы хотим, чтобы сеть обобщилась и относительно длины последовательности, и относительно количества повторений копирования. LSTM не справляется в обоих случаях, НМТ нормально отрабатывает более длинные последовательности, чем те на которых обучалась, и понимает более 10 повторений, однако, не может сохранить количество выданных копий и не правильно выдаёт маркер окончания.

Использование НМТ памяти при операции повторяющегося копирования:

Картина очень похожа на операцию копирования, вначале данные записываются в последовательные ячейки, а затем читаются из них, причем процедура чтения повторяется столько раз сколько необходимо. Есть еще одно отличие - белая точка в нижней части весов чтения, авторы полагают, что это соответствует промежуточной позиции, которая используется для перевода головки на начало последовательности (аналог оператора goto для НМТ).

Ассоциативная память

Первые два эксперимента показали, что НМТ может применять алгоритмы работающие с относительно простыми структурами. Новой задачей авторы хотят проверить сможет ли НМТ работать с более сложными нелинейными данными.

На вход сети подаётся от 2 до 6 элементов, каждый из которых состоит из трёх шестибитных чисел, чтобы разделять элементы между ними в сеть подаётся разделительный флаг. После того как все элементы последовательности переданы, передаётся ещё один элемент, который служит “запросом”, сеть должна отыскать этот элемент среди переданных ранее, и вернуть на выход элемент последовательности следующий за найденным.

Графики тренировки:

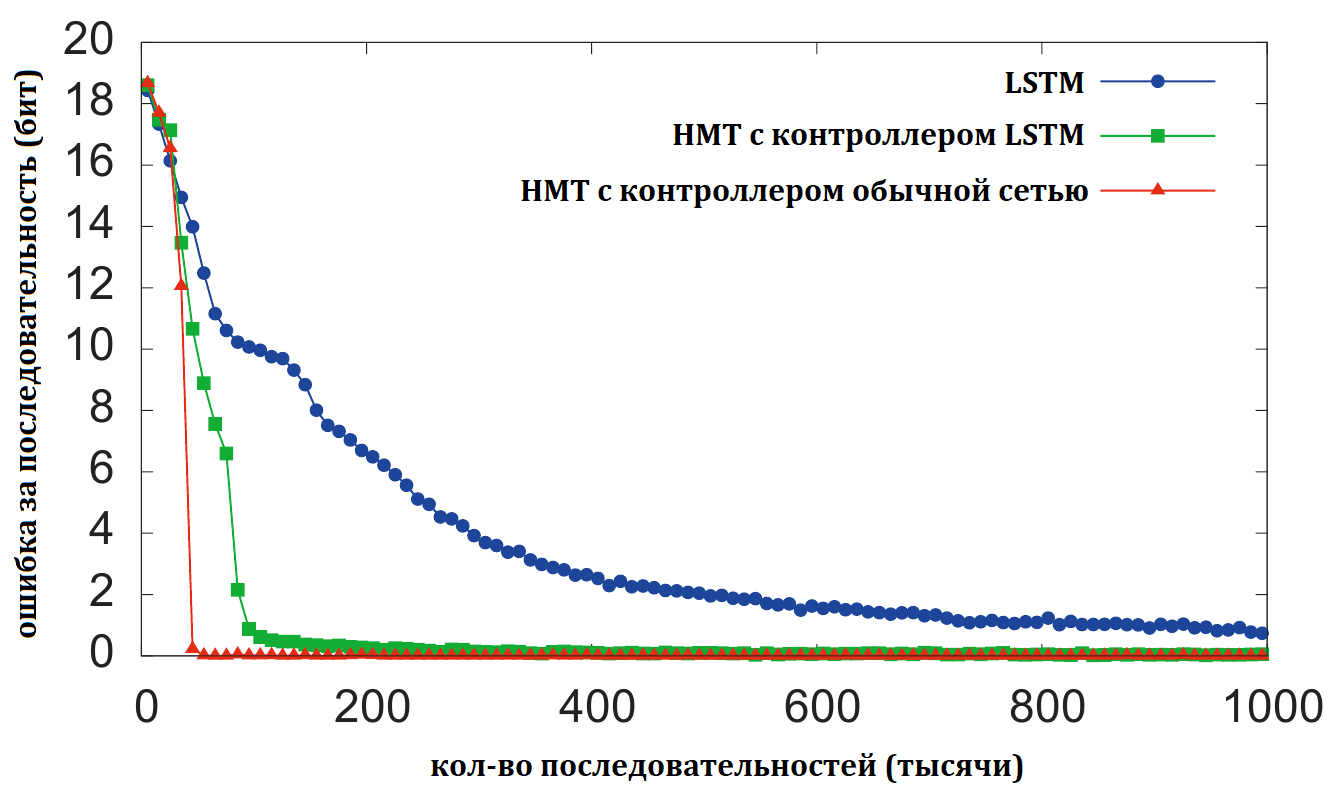
показывают, что НМТ сеть втренировывается до почти нулевой ошибки примерно за 30’000 итераций, простая LSTM не может сделать этого после 1’000’000 итераций. Так же из графика видно, что НМТ с контролером в виде обычной сети с прямой связью тренируется быстрее, чем вариант с LSTM контролером. Отсюда авторы делают вывод, что внешняя память НМТ более эфективный путь работы с данными, чем внутреннее состояние LSTM. Также НМТ лучше обобщается на длинные последовательности.

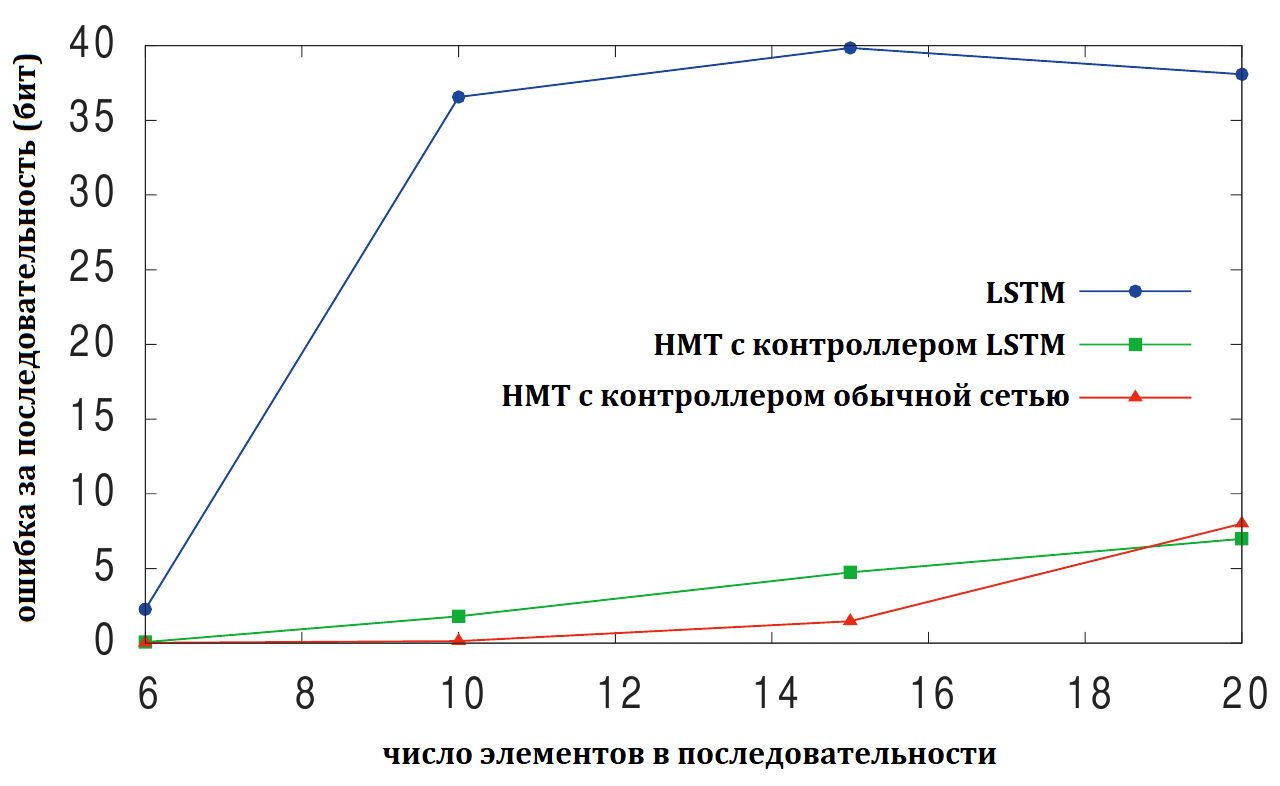
Из графика видно, что НМТ с контролером в виде обычной сети с прямой связью практически не ошибается на последовательностях вдвое длинее, чем те на которых она тренировалась.

Наконец, посмотрим на работу с памятью НМТ с контролером в виде LSTM сети, и одной головкой.

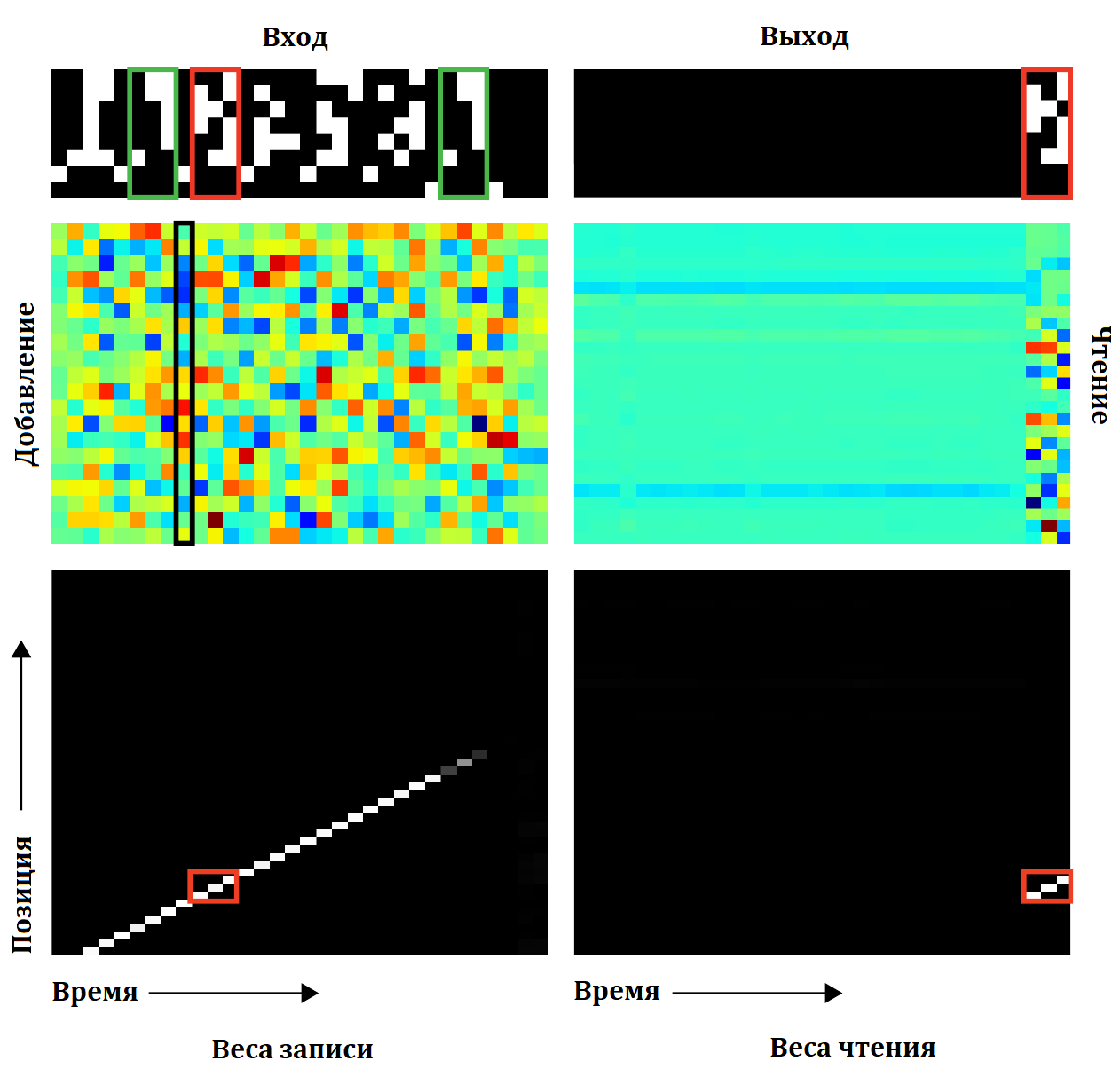
Разделителем элементов последовательности выступает байт с одним включенным шестым битом, а завершение последовательности обозначается байтом с включенным седьмым битом. Затем подаётся “запрос”, который в данном случае совпадает со вторым элементом последовательности, а значит на выход должен быть послан элемент номер три (в красной рамке). Веса чтения показывают, что на последних трех шагах сеть читает три последовательных байта из памяти позиция которых соответствует байтам записанным когда на вход сети пришел элемент номер три. Отметим, что сеть пишет в память даже когда на вход приходят те байты, которые соответствуют разделителям, а не самим элементам последовательности, причем если посмотреть внимательно в раздел “добавление” пишет она каждый раз разные вектора. Так же видно, что в нулевую ячейку памяти сеть первый раз записывает уже после того как пришли данные первого элемента последовательности. Наконец, вектор “запрос” практически не записывается во внешнюю память, а остаётся внутри контролера и используется для генерации весов для чтения.

Это приводит авторов к следующему объяснению работы сети. На каждый разделительный байт, сеть генерирует некоторое сжатое представление только что полученного элемента (что то вроде хеш функции) и записывает его в память. Когда приходит запрос, для него по тому же алгоритму вычисляется хеш, затем он ищется в памяти, и отдаются три байта следующие за хешом. По всей видимости в данном случае срабатывает вначале адресация по содержимому, а затем по позиции.

Сортировка

Сортировка данных - стандартная задача. На вход сети подаётся последовательность случайных бинарных векторов с приписанным каждому вектору приоритетом, приоритет выбирается равновероятно из отрезка $[-1, 1]$. На выходе сеть должна выдать те же бинарные вектора отсортированные в порядке приоритета. Входная последовательность содержит 20 пар (бинарный вектор и его приоритет) на выходе авторы ожидают 16 наиболее приоритетных векторов (этот момент я не особо понял, авторы пишут, что ограничили размер последовательности 16-ю векторами, потому что хотят увидеть будет ли НМТ решать задачу сортировки используя heapsort с глубиной 4, но откуда у них эта гипотеза не поясняют).

Графики тренировки:

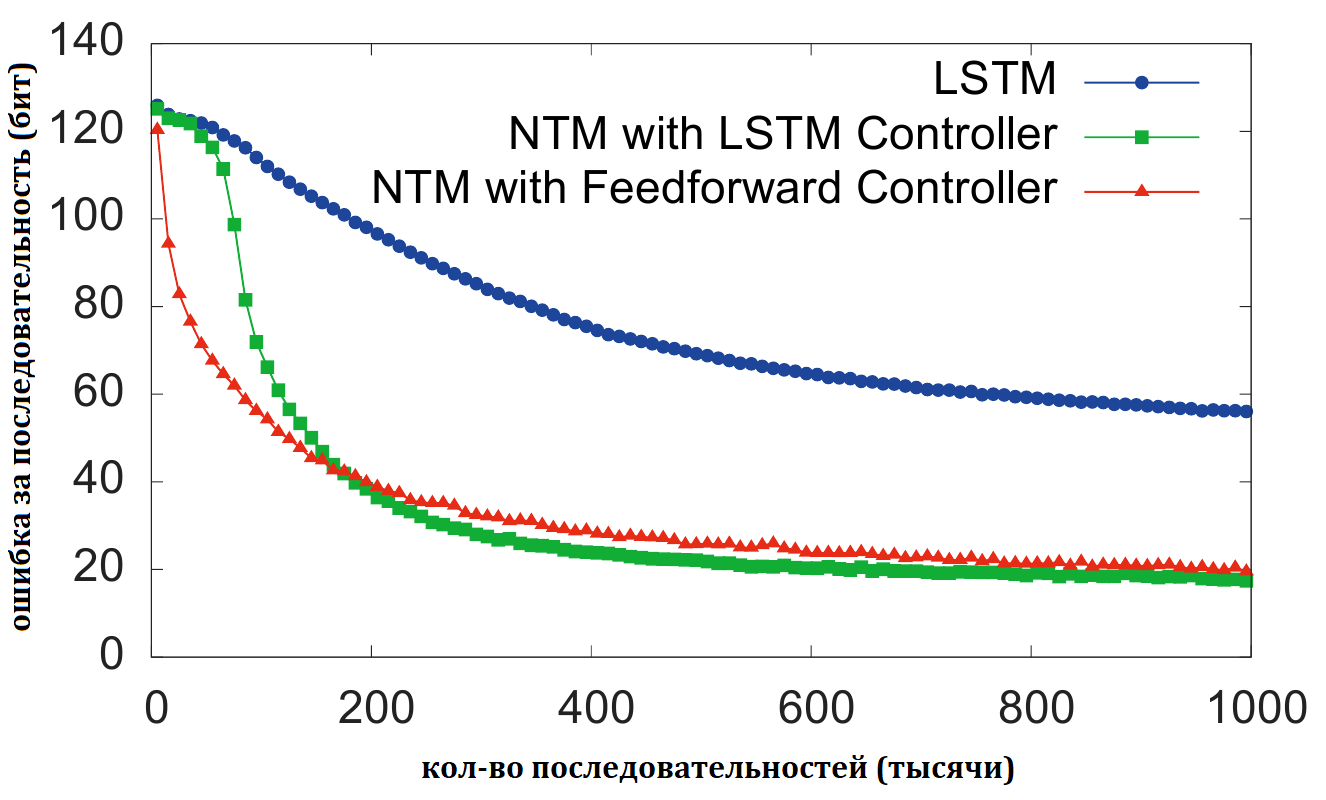
Снова НМТ в обоих вариантах втренировывается лучше чем обычный LSTM.

В данном случае авторы предлагают использовать 8 читающих и пишущих головок для достижения лучшего качества.

Выводы

Нейронная машина Тьюринга демонстрирует весьма интересный подход с дополнительной памятью, используемой нейронной сетью. Важно, что представленный вариант сети остаётся дифференцируемым, а значит мы можем натренировать его в обычным способом - обучения с учителем. Так же важно, что на тех простых алгоритмах, которым сеть получилось научить, сеть умеет обобщаться и работать в ситуациях не представленных в тренировочных данных.