arXiv:2104.06405

Еще одно продолжение NeRF, авторы этой статьи обращают внимание, что для получения хорошего представления 3D сцены при помощи нейронной сети, как это описано в NeRF необходимо, чтобы исходный набор изображений имел очень точные координаты камер. Однако в реальной ситуации далеко не всегда точные координаты места съёмки известны. Авторы предлагают способ тренировки нейронной сети типа NeRF, который может иметь дело с не вполне точными координатами камер.

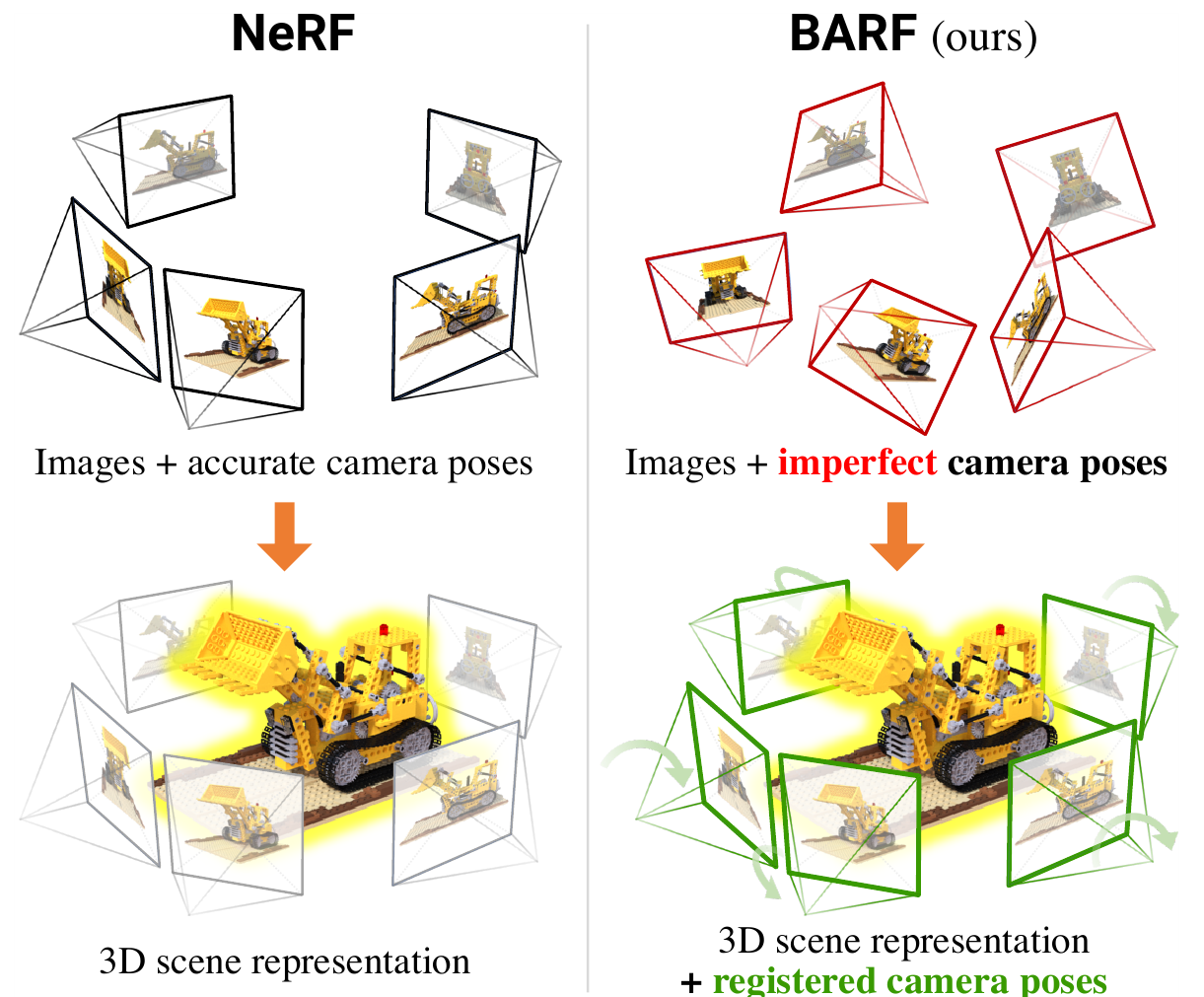
Авторы обращаются к опыту SfM и SLAM алгоритмов, в которых используется bundle adjustment техника, т.е. глобальная оптимизация, которая уточняет и координаты найденных трёхмерных точек и одновременно позицию камеры в момент съёмки.

Чтобы проделать тоже самое для решения задачи получения 3Д представления по набору изображений, авторы включают зависимость от позиции камеры в процесс тренировки.

Итак NeRF кодирует 3Д сцену при помощи нейронной сети: $f: \mathbb{R}^3 \rightarrow \mathbb{R}^4$, которая для точки $x \in \mathbb{R}^3$ отдаёт RGB цвет $c \in \mathbb{R}^3$ и плотность $\sigma \in \mathbb{R}$ в этой точке. Т.е. $y = (c, \sigma)^T = f(x, \Theta)$, где $\Theta$ - это параметры сети, которые мы планируем натренировать.

Теперь для того чтобы получить цвет изображения $\mathcal I(u)$ в двумерной точке $u$, используем формулу:

\[\tilde {\mathcal I}(u) = \int_{t_n}^{t_f} T(u, t) \cdot \sigma(t \bar u) \cdot c(t \bar u) dt, \, где \, T(u, t) = \exp \left(-\int_{t_n}^{t_f}\sigma(s\bar u)ds\right)\]

$\bar u = (u; 1)^T \in \mathbb{R}^3$ - гомогенные координаты для точки $u \in \mathbb{R}^2$ на изображении, и тогда $t \bar u$ это луч, из камеры через точку $u$. Чтобы получить численное значение интеграла, отрезок интегрирования разбивается на части в каждой части выбирается точка, т.о. получается набор точек параметризованных при помощи $\{t_1, t_2, …, t_N\}$, для этих точек, при помощи сети мы получим значения: $\{y_1, y_2, …, y_N\}$, т.ч. $y_i \in \mathbb{R}^4$. И можно записать представление цвета пикселя изображения в виде функции: $\tilde {\mathcal I}(u) = g(y_1, y_2, …, y_N)$. При этом $g:\mathbb{R}^{4N} \rightarrow \mathbb{R}^3$ дифференцируема и не зависит от параметров, которые можно обучать.

Теперь вернемся к координатам точки. Пока мы использовали трехмерные координаты точек в системе координат, привязанной к камере, но в нейронную сеть надо подавать координаты в некоторой “мировой системе координат”. Камеру в трехмерном пространстве можно описать при помощи набора параметров $p \in \mathbb R^6$. А значит, используя $p$ можно определить преобразование $\mathcal W(\cdot, p): {\mathbb R}^3 \rightarrow {\mathbb R}^3$ из координат точки в системе координат камеры в мировые координаты. И тогда функция генерации цвета пикселя, будет зависить ещё и от параметров камеры и выглядеть следующим образом:

\[\tilde {\mathcal I}(u, p) = g\left(f\left(\mathcal W(z_1\bar u, p), \Theta) \right), f\left(\mathcal W(z_2\bar u, p), \Theta) \right), ..., f\left(\mathcal W(z_N\bar u, p), \Theta) \right)\right)\]

Если у нас есть $M$ изображений $\{ \mathcal I_i \}_{i=1}^M$, то надо решить задачу оптимимзации:

\[\min_{p_1, ..., p_M, \Theta} \sum_{i=1}^M\sum_u \vert\vert \tilde {\mathcal I}(u, p_i, \Theta) - {\mathcal I}_i(u)\vert\vert^2_2\]

Итак с задачей определились. Теперь несколько замечаний о подходе к решению.

Возвращаясь к оригинальной статье про NeRF надо напомнить, что её авторы предлагали (и это являлось одним из существенных шагов для повышения качества) подавать на вход сети не просто трёхмерные координаты, а вектор:

\[\gamma(x) = (x, \gamma_0(x), \gamma_1(x), ... , \gamma_{L-1}(x)) \in \mathbb{R}^{3+6L}\]

в котором $k$-ая координата:

\[\gamma_k(x)=\left(\cos\left(2^k\pi x\right), \sin\left(2^k\pi x\right)\right) \in \mathbb{R}^6\]

Производная такой функции будет:

\[\frac{\partial \gamma_k(x)}{\partial x} = 2^k\pi \cdot \left(-\sin\left(2^k\pi x\right), \cos\left(2^k\pi x\right)\right)\]

Соответственно градиент, полученный от сети увеличится в $2^k\pi$ раз и поменяет направление в соответствии с частотой и авторы данной статьи пишут, что это приводит к проблемам определения сдвига $\Delta p$ для параметров камеры, поскольку сигналы из разных 3Д точек некогерентны и могут погасить друг друга. Чтобы избежать этих проблем, предлагается добавить весовой коэффициент в функцию $\gamma_k(x)$:

\[\gamma_k(x, \alpha)=\omega_k(\alpha)\left(\cos\left(2^k\pi x\right), \sin\left(2^k\pi x\right)\right)\]

коэффициент определяется следующей формулой:

\[\omega_k(\alpha) = \begin{cases} 0, & \alpha < k\\ \frac {1 - \cos((\alpha - k)\pi)} 2, & 0 \le \alpha - k < 1 \\ 1, & \alpha - k \ge 1 \end{cases}\]

Такой вариант отсекает координаты, модулированные высокими частотами, т.е. в каком-то смысле работает как низкочастотный фильтр, аналогично тому, как, например, при решении задачи поиска оптического потока, мы вначале ищем приближение на уменьшенных изображениях (или что тоже самое изображениях с отброшенными высокими частотами), а потом используем результат поиска как начальное приближение для следующего шага с большим масштабом. В данном случае увеличивая $\alpha \in [0, L]$ с течением времени, в сеть подаются координаты точки модулированные всё более высокой частотой. И поскольку градиент примет вид:

\[\frac{\partial \gamma_k(x, \alpha)}{\partial x} = \omega_k(\alpha) \cdot 2^k\pi \cdot \left(-\sin\left(2^k\pi x\right), \cos\left(2^k\pi x\right)\right)\]

то для части частот, для которых $\omega_k(\alpha) = 0$ он занулится, это позволит на начальном этапе получить хорошие сдвиги для параметров камеры, а значит эффективно уточнить их позиции.

Эксперименты

Первый эксперимент авторы провели на тех же 8 синтетических сценах, которые использовались в оригинальной статье про NeRF. Они случайным образом сдвинули и повернули камеры, в рамках нормального распределения ошибки с центром в нуле и среднеквадратичным отклонением для поворота $14.9^{\circ}$ и $0.26$ для сдвига.

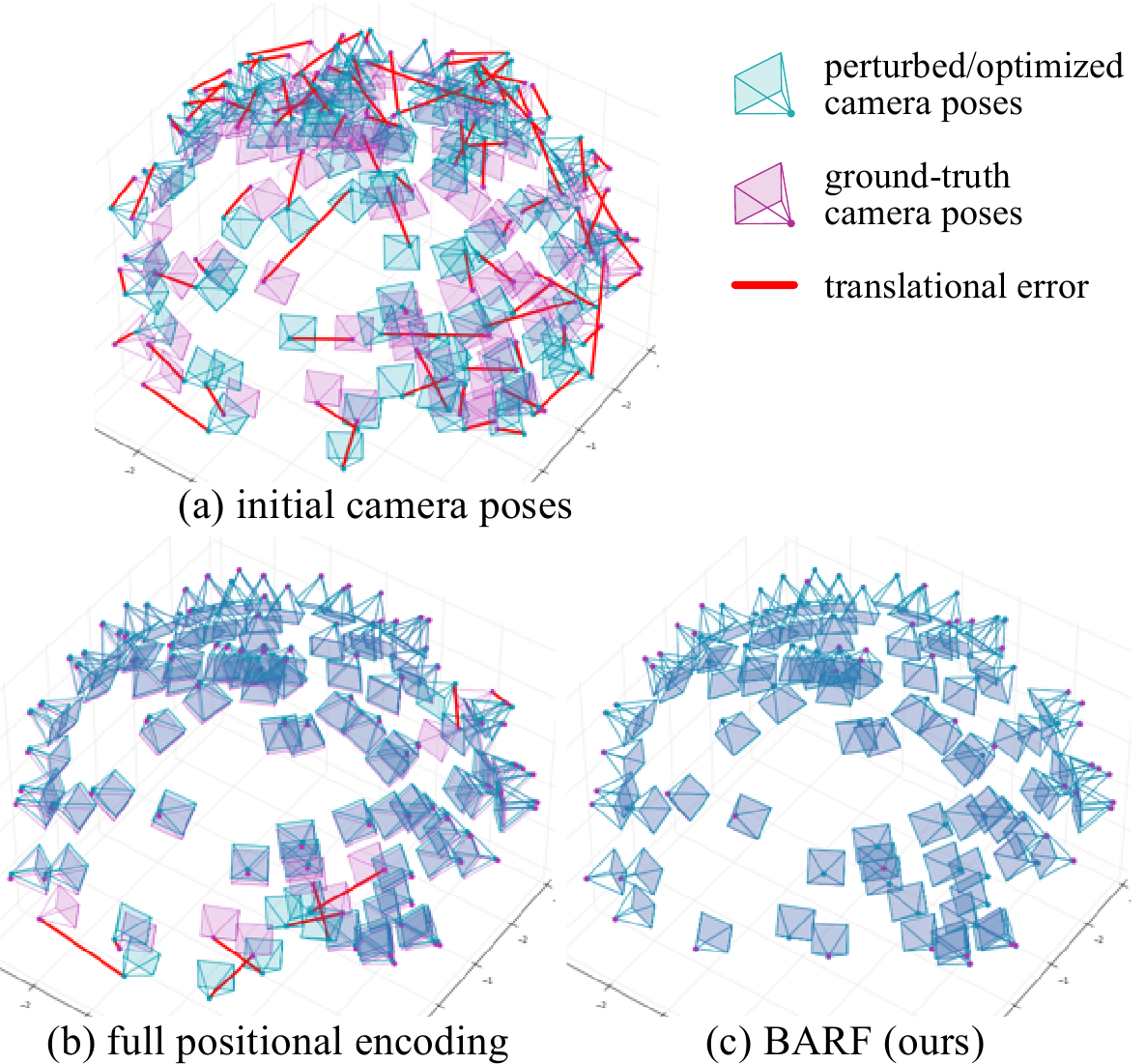
После прогона алгоритма, получилось сравнимое с NeRF (который тренировался на точных позициях камер) качество картинки, и достаточно точное восстановление позиций камер (меньше одного градуса ошибка поворота).

Второй эксперимент проводился на фотографиях реального мира (из датасет LLFF), при этом позы камер в данном наборе полученны при помощи SfM алгоритма, т.е. результат работы BARF сравнивался в данном случае не с некими реальными данными, а с тем, как эти данные приближает хороший алгоритм SfM.

В этом эксперименте BARF вновь продемонстрировал хорошие результаты и по восстановлению позиций камер (исходно все параметры камеры задавались равными нулю) и по тренировке сети для представления трехмерной сцены. Результаты в сравнении с NeRF (с точными позициями камер восстановленными при помощи SfM):

Карты глубин показывают, что и позиции камер BARF восстановил очень хорошо.