arXiv:1612.01022

Cтатья решает задачу предсказания пробок (в достаточно простой постановке). Есть дорога без разветвлений и перекрёстков. На этой дороге отмечен некий набор контрольных точек, в которых каждые 5 минут замеряется traffic volume

Надо на основе значения величины в контрольных точках в текущий момент и в прошлом, предсказать значение traffic volume в будущем.

Для решения задачи авторы предлагают объединить два типа сети: одномерную свёрточную сеть и рекуррентную LSTM сеть.

Схема работы выглядит следующим образом:

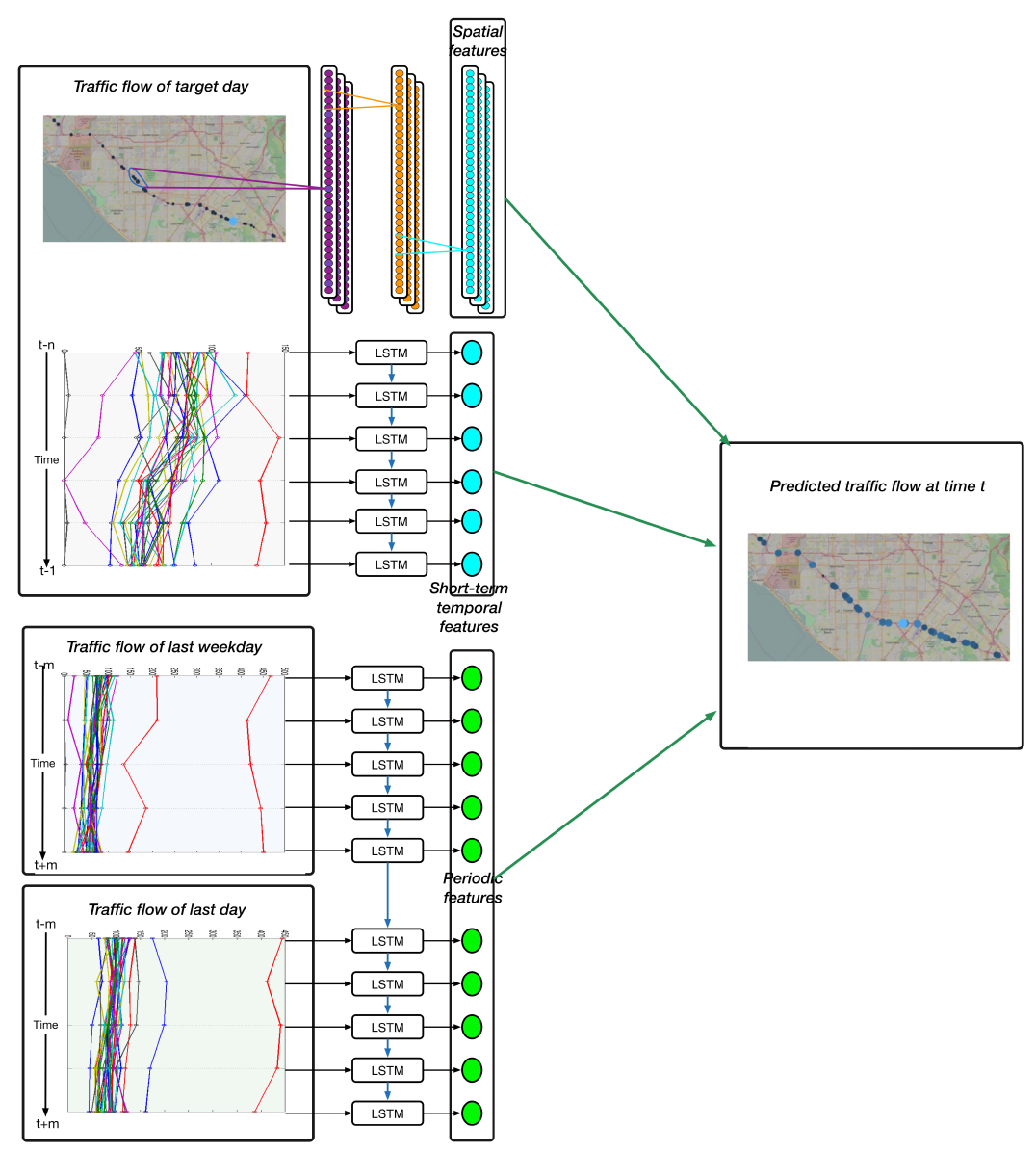
Итак у нас есть замеры в $p$ точках: $\{s_i(t)\}_{i=1}^p$ в моменты времени $(t-n, t-n+1, …, t-1)$ и нам надо предсказать значения той же величины traffic volume в этих точка в моменты времени $(t, t+1, …, t+h)$. Имеющиеся замеры можно представить в виде матрицы:

\[S = \begin{bmatrix} s_1(t-n)& s_1(t-n + 1)& ... & s_1(t-1)\\ s_2(t-n)& s_2(t-n + 1)& ... & s_2(t-1)\\ \vdots & \vdots & & \vdots\\ s_p(t-n)& s_p(t-n + 1)& ... & s_p(t-1)\\ \end{bmatrix}\]

Очевидно, пробки в данной точке зависят от значения в ней и от значения в её соседях. Поэтому авторы предлагают рассмотреть матрицу $S$ как $n$- канальный (по количеству временных отсчётов) одномерный сигнал: $T_q = \left[s_1(t-n+q), s_2(t-n+q),…, s_p(t-n+q)\right]^T$ ($0 \le q \le n-1)$), к которому можно применить одномерную свёрточную сеть, в результате снова получим одномерный сигнал с некоторым количеством каналов (по количеству фильтров свёрточной сети), для получения более сложных откликов, можно использовать несколько таких слоёв. При этом, в свёрточной сети авторы не пытаются выделить временные связи, а только пространственные, т.е. преобразование на слое $k$ выглядит следующим образом:

\[h_q^k = o(\omega_q^k \ast T_q^k + b_q^k)\]

здесь $\omega_q^k$ - веса, $b_q^k$ - свободный член, $\ast$ - свёртка, а $o(\cdot)$ - нелинейность.

Временную зависимость предполагается отслеживать, используя LSTM сеть. Авторы берут вариант LSTM с forget gate и peephole connection. На вход последовательно подаются всё теже вектора $T_q$ начиная с самого “старого” по времени $T_0$ и до $T_{n-1}$, на выходе получим последовательность откликов: $H = (H_0, H_1, …, H_{n-1})$.

Так же авторы предлагают учесть тот факт, что величина пробки имеет некую периодичность, поэтому они предлагают взять еще два набора значений:

\[S^d = \begin{bmatrix} s_1(t^d-n^d)& s_1(t^d-n^d + 1)& ... & s_1(t^d-1)\\ s_2(t^d-n^d)& s_2(t^d-n^d + 1)& ... & s_2(t^d-1)\\ \vdots & \vdots & & \vdots\\ s_p(t^d-n^d)& s_p(t^d-n^d + 1)& ... & s_p(t^d-1)\\ \end{bmatrix}\]

это значение пробки взятые в тоже время, но на день раньше ($t - t^d$ равно 24 часам), и

\[S^w = \begin{bmatrix} s_1(t^w-n^w)& s_1(t^w-n^w + 1)& ... & s_1(t^w-1)\\ s_2(t^w-n^w)& s_2(t^w-n^w + 1)& ... & s_2(t^w-1)\\ \vdots & \vdots & & \vdots\\ s_p(t^w-n^w)& s_p(t^w-n^w + 1)& ... & s_p(t^w-1)\\ \end{bmatrix}\]

это значения пробки в тоже время, но неделю назад. Таким образом у нас появилось еще два набора векторов $\{T^d_q\}_q$ и $\{T^w_q\}_q$, которые авторы предлагают так же прогнать через LSTM сеть, причем, предполагая наличие корреляции между этими двумя наборами, авторы добавляют связь из LSTM для предыдущего дня в LSTM для пробок неделю назад.

Теперь отклики от CNN и трёх LSTM объединяются, и подаются на последний слой, который должен выдать предсказание для пробок в наших контрольных точках в момент времени $t$.

В качестве штрафной функции для тренировки сети берётся сумма квадратов разностей между предсказанными значениями пробки и реальными (проще говоря, $\vert\vert \cdot \vert\vert^2_2$).

Эксперименты авторы проводили на наборе PeMS, в нем в 33 контрольных точках собирается значение пробки агрегированное за пять минут (т.е. 288 значений в одной точке за сутки).

Размер временного окна для $S$ был выбран $n = 15$ (т.е. 75 минут назад). Для $S^d$ и $S^w$ размер временного окна был выбран одинаковым: $n^d = n^w = 6$ (т.е. 30 минут).

Свёрточная сеть собрана из трех слоёв, по $30$ фильтров в каждом слое, ширина свёртки для первых двух слоёв равна $3$, для последнего $2$. Для LSTM сети текущего дня (на наборе $S$) размерность вектора откликов ($H_i$) выбрана равной $40$. Для LSTM сетей предыдушего дня и прошлой недели (на наборах $S^d$, $S^w$) размерность вектора откликов выбрана равной $25$.

Авторы показывают, что качество данного подхода лучше чем обычный LSTM, но правда всего на 1-1.5%.

Статья интересная, но с моей точки зрения слабо применима к реальной проблеме, особенно внутригородской, потому что работает с “коридором”, что позволяет применить обычную одномерную свёрточную сеть. Для более общей ситуации, надо будет заменять одномерный вариант, на что-то вроде GNN и это существенно усложнит решение.