arXiv:1812.11118

Сегодня разберём статью, посвященную классической проблеме статистического обучения: компромисса смещения-дисперсии (bias-variance trade-off), рассматриваемую в приложении к современным методам машинного обучения. Оказывается, что классическая интуиция в подборе модели - модель должна быть не слишком простой, чтобы суметь описать структуру данных (т.е. не должно произойти “недообучения”), но и не слишком сложной, чтобы не переобучиться на тренировочные данные и суметь обобщиться - так вот эта интуиция для современных моделей, таких как нейронные сети - не работает.

Нейронные сети представляют из себя весьма богатые модели и зачастую обучаются до такой степени, что на тренировочных данных ошибки практически отсутствуют, такая ситуация в классической интерпретации рассматривалась бы как переобучение, однако, такие переобученные сети показывают высокую точность и на тестовых данных.

В данной статье, авторы предлагают концепцию двойного спуска (double descent): если изобразить зависимость ошибки на тестовых данных от сложности модели в виде кривой, то в левой части такого графика мы имеем классическую U кривую - при увеличении сложности модели ошибка вначале уменьшается, а затем начинает расти. Однако, если продолжить увеличивать сложность модели, то ошибка на тестовых данных, с некоторого момента, вновь начинает спадать - получается второй спуск.

Введение

Классическую задачу машинного обучения - предсказание - можно сформулировать следующим образом: пусть у нас есть набор тренировочных данных вида $(x_1, y_1), (x_2, y_2),…,(x_n, y_n)$ из $\mathbb{R}^d \times \mathbb{R}$, необходимо обучить на этих данных функцию $h_n: \mathbb{R}^d \rightarrow \mathbb{R}$, чтобы уметь предсказывать значение метки $y$ для точек $x \in \mathbb{R}^d$, которых не было в тренировочном наборе.

Обычно фиксируется некоторый набор/класс функций ${\mathcal H}$ (например, нейронные сети определенной структуры), и решение задачи ищется в этом наборе. При этом в качестве хорошо предсказывающей функции ищут функцию $h(x)$ из ${\mathcal H}$ минимизирующую эмпирический риск, т.е. такую, которая решает задачу оптимизации:

\[\frac 1 n \sum_{j=1}^N l(h(x_j), y_j) \rightarrow \min,\, h \in {\mathcal H}\]

здес $l(y’, y)$ некоторая штрафная функция, которую обычно выбирают исходя из физического смысла задачи, например, для задачи регрессии часто используют квадрат ошибки: $l(y’, y) = (y’ - y)^2$, а для классификации кроссэнтропию или zero-one штраф: $l(y’, y) = \mathbb{1}_{y’\neq y}$.

Традиционно считается, что в зависимости от “приёмистости” класса ${\mathcal H}$ можно выделить два плохих случая:

1. Если класс ${\mathcal H}$ малопредставителен, то предсказатели из этого класса не смогут хорошо минимизировать эмпирический риск, а, следовательно, и предказывать метки вне тренировочного набора точек тоже будут плохо. Имеем ситуацию недообученности (underfiting).

2. Если класс ${\mathcal H}$ слишком богатый, то может получиться ситуация переобучения (overfiting), когда находится предсказатель для которого эмпирический риск близок или даже равен нулю, но при этом на данных из того же распределения, не входящих в тренировочный датасет, предсказатель работает плохо.

Поэтому класс ${\mathcal H}$ рекомендуется (в классическом машинном обучении) выбирать где-то между этими двумя случаями: недо- и пере- обучения (компромисс смещения-дисперсии). Делается это либо напрямую (например, выбором модели нейронной сети), либо косвенно (например, используя методы регуляризации, раннюю остановку и т.п.). Эту ситуацию графически можно описать как U-кривую риска:

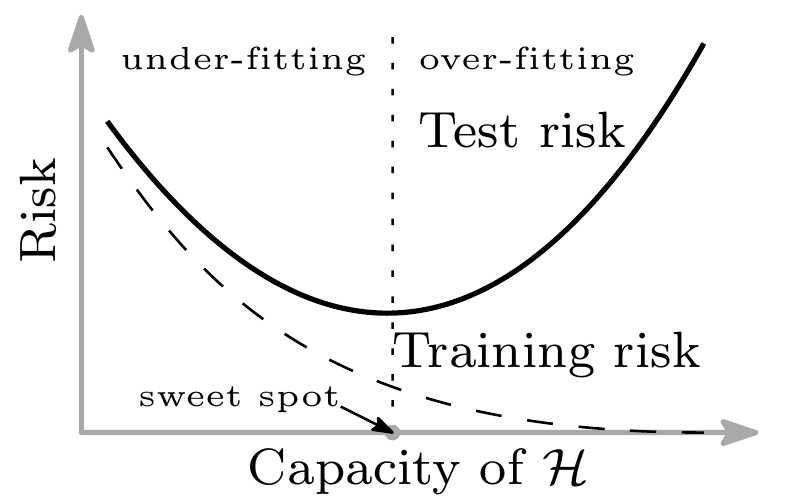
Т.е. в классическом машинном обучении считается, что если ошибка на тренировочных данных близка к нулю, то скорее всего модель для этой задачи слишком сложная и мы попали в ситуацию переобучения, надо либо упрощать модель, либо набирать больше данных. Однако, современные модели, например, нейронные сети, могут очень хорошо втренироваться, вплоть до того, что получить эмпирический риск равный нулю, при этом показывать отличную точность на тестовых данных, которые никогда не видели. Соответственно, для нейронных сетей обычно выбирают как раз модель, которая сможет на тренировочных данных опустить эмпирический риск до нуля. Более того, часто “сложные” модели натреннированные таким образом, показывают хорошие результаты даже, если тренировочные данные были зашумлены.

В данной статье, авторы исследуют зависимость качества предсказания от широты класса ${\mathcal H}$ из которого выбираются модели. Они показывают, что эту зависимость (строго говоря для некоторого класса, исследованных ими моделей) можно изобразить в виде графика двойного спуска:

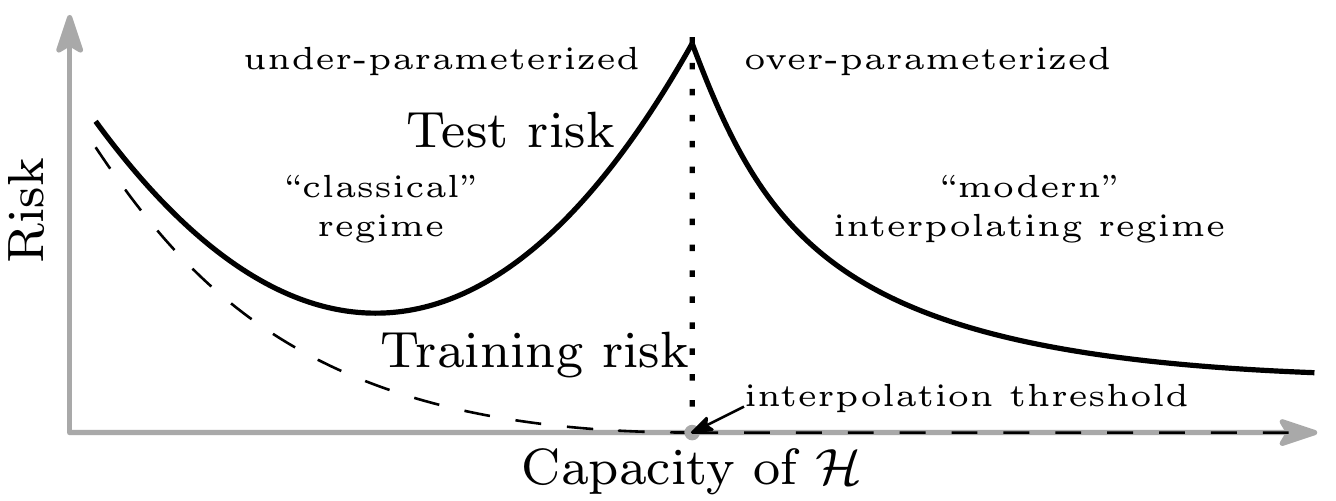
Видно, что кривая включает себя классическую U кривую, однако, если продолжать усложнять модель за пределы порога интерполяции (interpolation threshold), то ошибка на тестовых данных вновь начинает падать и, в конечном итоге, качество предсказателя с увеличением его сложности становится лучше, чем качество предсказателя сложность которого выбирали на основе компромисса смещения-дисперсии в нижней точке классической U кривой.

Нейронные сети

Random Fourier Features

Начинают авторы взяв в качестве класса моделей ${\mathcal H}_N$ - Random Fourier Features (см. “Random features for large-scale kernel machines”). Это функции $h: \mathbb{R}^d \rightarrow \mathbb{R}$ представимые в виде суммы:

\[h(x) = \sum_{k=1}^N a_k \phi(x, v_k),\, \phi(x, v) = e^{i\, v^T x}\]

$v_1, v_2, …, v_N$ - вектора выбранные независимым случайнным образом из стандартного нормального распределения на $\mathbb{R}^d$.

Углубляться в то, что представляет из себя данный класс функций не будем, но в след за авторами статьи отметим, что во-первых, функции данного класса можно рассматривать как нейронные сети из двух слоёв с фиксированными весами первого слоя. Во-вторых, при $N \rightarrow \infty$ мы получим класс функций ${\mathcal H}_{\infty}$ - гильбертово пространство с воспроизводящим ядром, у которого воспроизводящее ядро есть функция Гаусса.

Замечание. Пусть ${\mathcal H}$ — гильбертово пространство, состоящее из комплекснозначных измеримых функций, заданных на множестве $\Omega \in \mathbb{C}$. Термин “гильбертово пространство с воспроизводящим ядром” означает, что функционал $\delta_{\xi}$, который любой функции $f \in {\mathcal H}$ ставит в соответствие значение функции $f$ в точке $\xi \in \Omega$, является линейным и непрерывным функционалом для произвольной точки $\xi \in \Omega$. Пространство ${\mathcal H}$ имеет воспроизводящее ядро, т. е. функцию $K_{\mathcal H}(t, \xi)$, определенную для всех $(t, \xi) \in \Omega \times \Omega$ и такую, что для любого $\xi \in \Omega$, $K_{\mathcal H}(\cdot, \xi) \in {\mathcal H}$ и для любой $f \in {\mathcal H}$ выполнено соотношение: $\left(f, K_{\mathcal H}(\cdot, \xi)\right)_{\mathcal H} = f(\xi)$.

В данном случае сложность или “приёмистость” модели оценивается как $N$ - количество слагаемых.

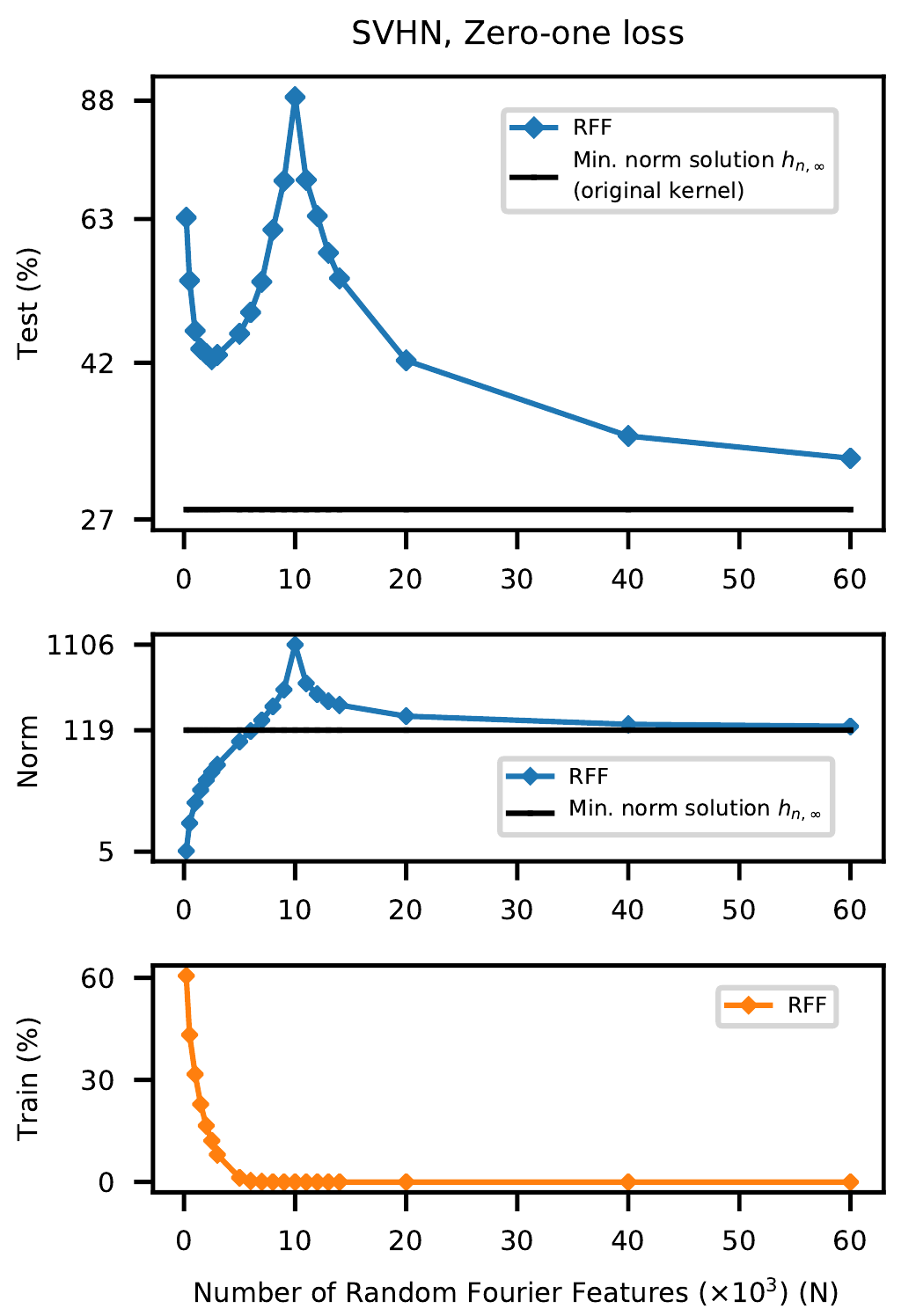
Авторы тренирует данную модель на датасете MNIST ($n = 10^4$, 10 классов) для разных значений $N$. Когда $N > n$ функция $h \in {\mathcal H}_N$, решающая задачу минимизации не будет единственной и авторы выбирают ту, для которой $l_2$-норма последовательности коэффициентов $(a_1, …, a_N)$ будет минимальной.

Результаты объеденены в графики:

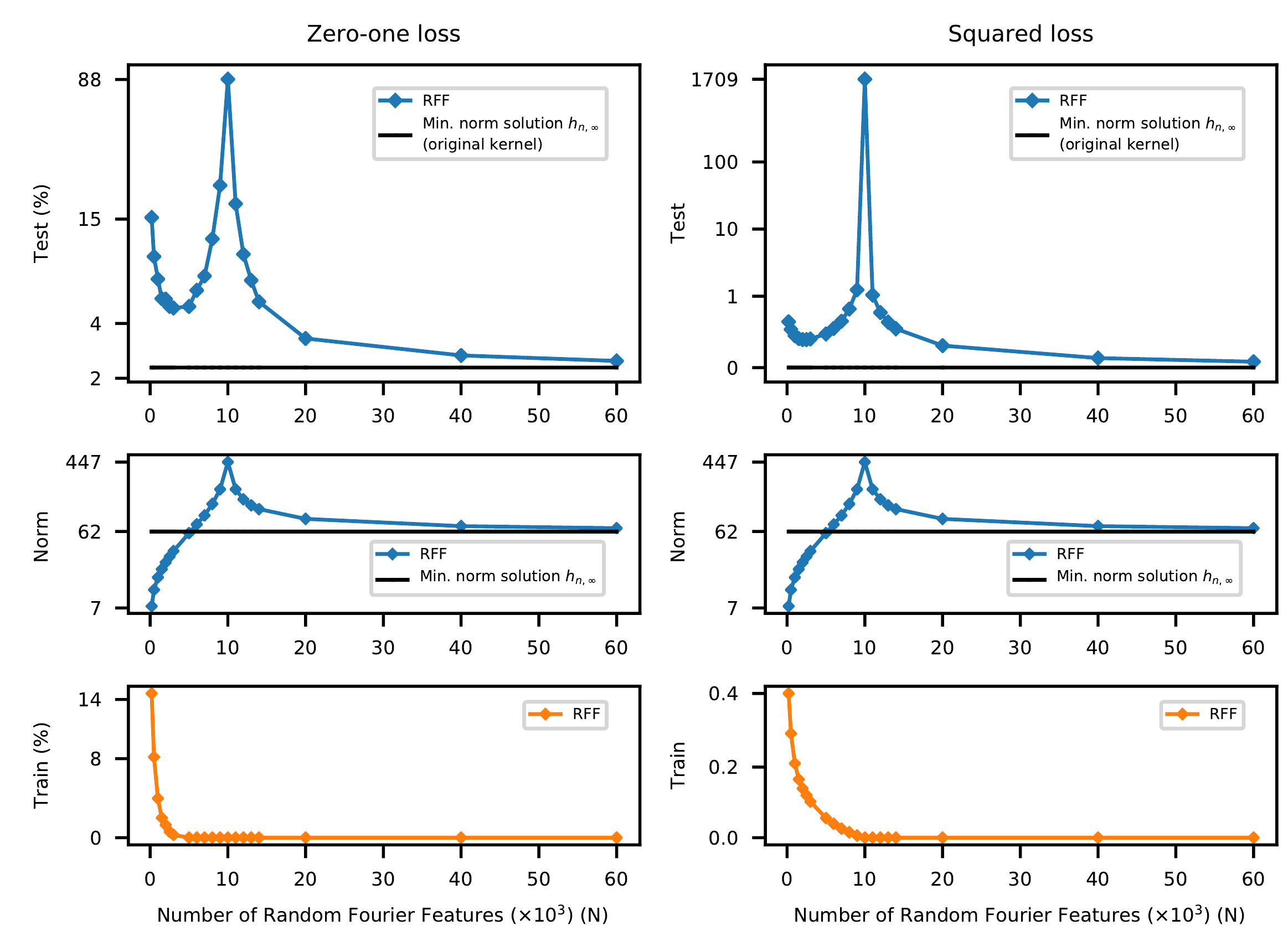
на графиках представлены зависимости процента ошибок и значения штрафной функции (здесь это среднеквадратичная ошибка) от размера модели, для тренировочных и тестовых данных, а также $l_2$ норма коэффициентов $a_k,\, k=1,…,N$. В качестве базовой модели на графике отображаются те же зависимости для предсказателя (с минимальной нормой) выбранного из ${\mathcal H}_{\infty}$.

Видно, что для $N \ll n$ работает классическая теория - вначале, с ростом сложности модели ошибка на тренировочных данных уменьшается, а качество предсказания на тестовых данных растет. Затем, начиная с некоторого момента, сложность модели становится такой, что она “перетренировывается”, т.е. ошибка на тренировочных данных уменьшается, но качество предсказания на тестовых данных начичнает ухудшаться. Наконец, начиная с некоторой сложности можно наблюдать второй спуск на котором увеличение сложности модели вновь приводит к улучшению качества, хотя казалось бы на тренировочных данных минимум ошибки достигнут на моделях с существенно меньшей сложностью.

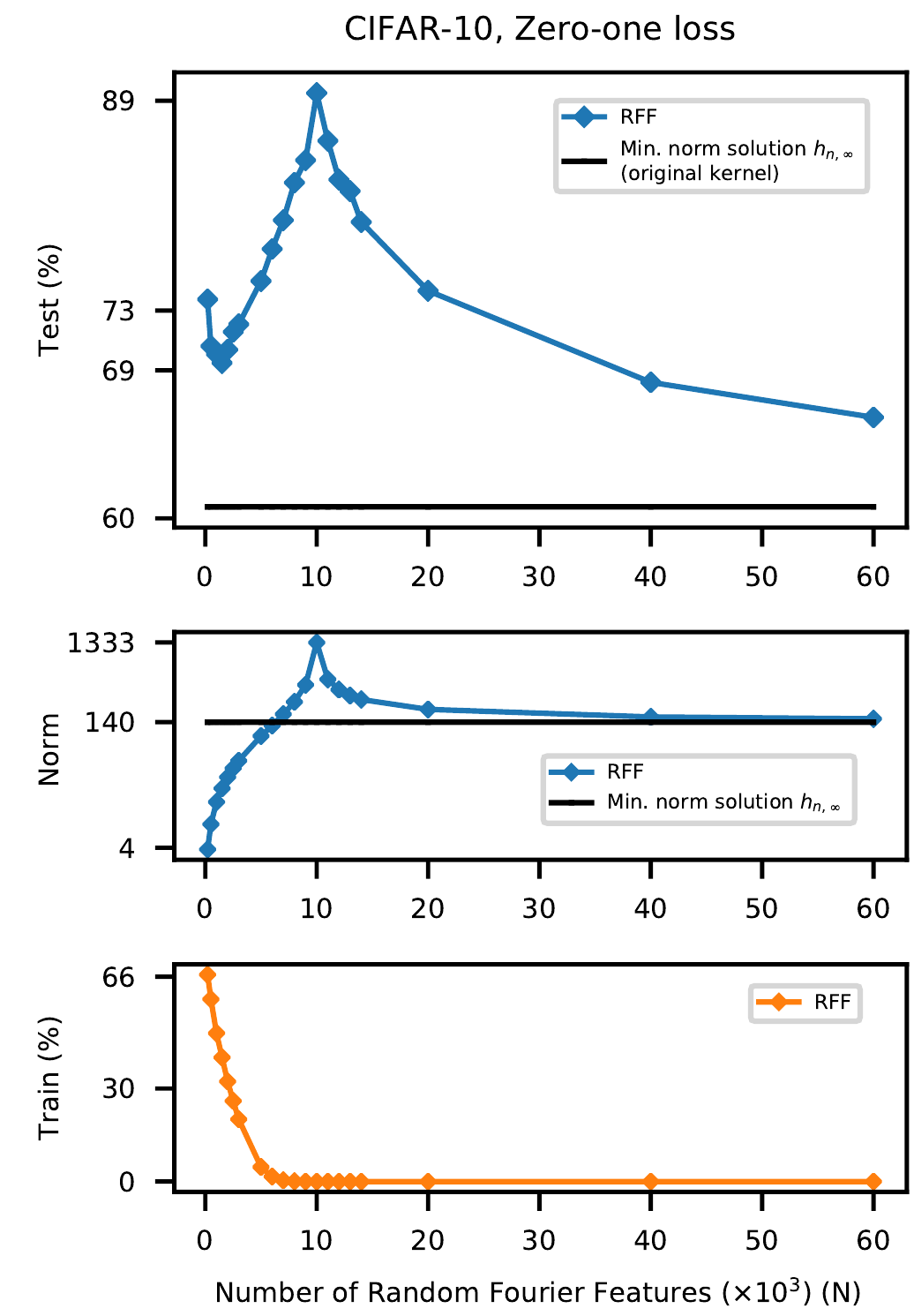
Авторы также натренировали RFF на некоторых других датасетах и во всех случаях получили схожие графики:

Обычная нейронная сеть

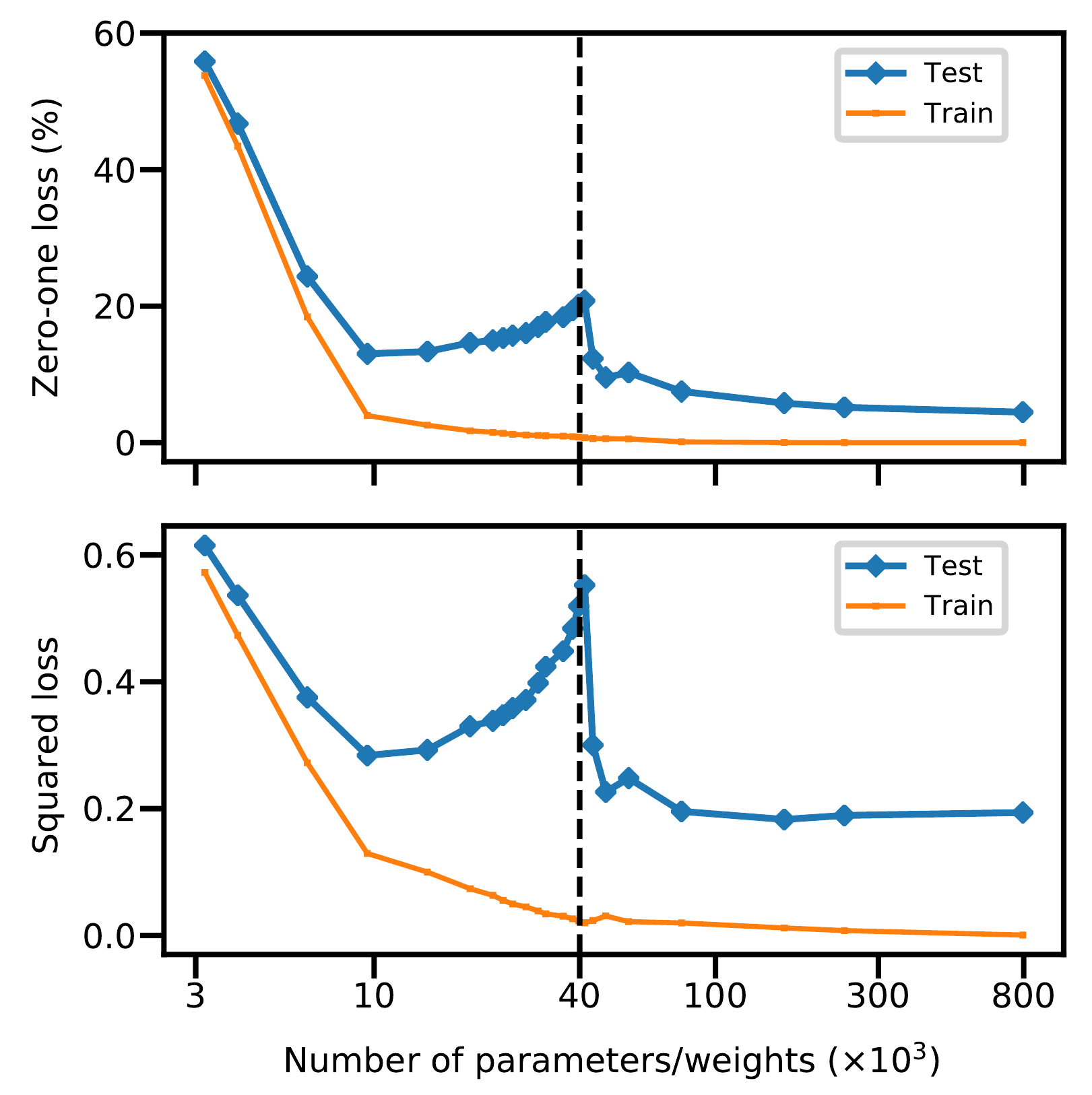
Следующий эксперимент авторы проводят на обычной полносвязной нейронной сети с одним скрытым слоем. Количество нейроннов $H$ скрытого слоя в данном случае характеризуют сложность модели. В качестве датасете для обучения используется подмножество из MNIST ($n=4 \cdot 10^3$, $d=784$, $K=10$ классов). Число параметров нейронной сети будет $(d+1)\cdot H + (H+1)\cdot K$. На графике авторы вертикальной прерывистой линией обозначили $N = n\cdot K$ - для которого наблюдается порог интерполяции:

Решающие деревья и ансамбли

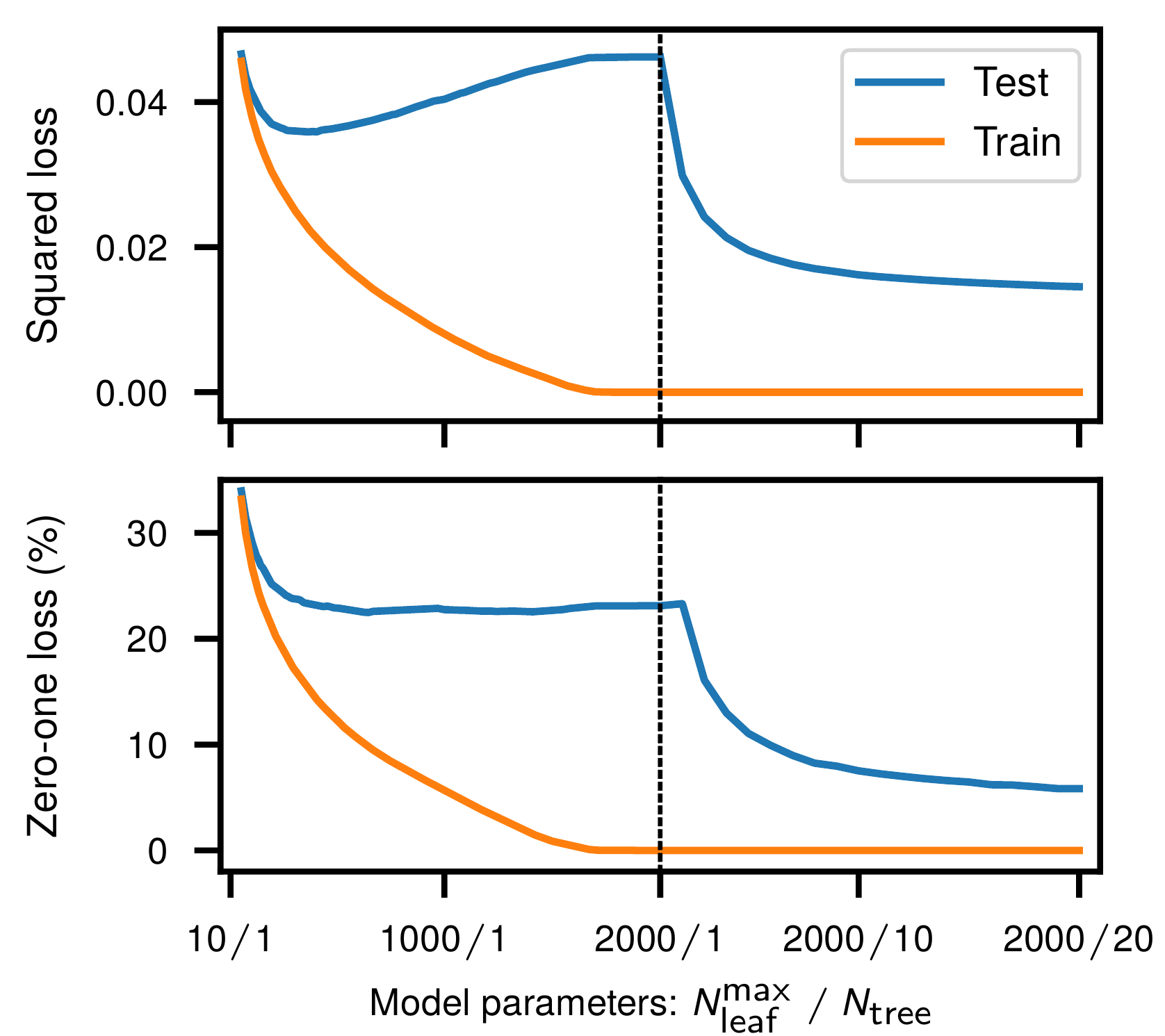
Авторы проводят аналогичный эксперимент со случайным лесом (random forest) из решающих деревьев, регулируя сложность модели высотой (количеством листов) дерева и количеством деревьев в лесу. В качестве датасета вновь используется подмножество из MNIST ($n=10^4$, 10 классов) и снова на графике можно наблюдать кривую двойного спуска:

Выводы

Таким образом авторы своей теорией двойного спуска увязывают классическую дилемму смещения-дисперсии и наблюдаемое улучшение качества предсказания при использовании сложных моделей нейронных сетей.