Продолжим разбираться с многоруким бандитом. Разберем способ оценки математического ожидания в случае когда распределение случайной величины меняется со временем, а также посмотрим как влияет на жадную стратегию выбор начальной оценки математического ожидания награды.

Меняющиеся со временем награды

Вернемся к вычислению математического ожидания некоторой случайной величины. Мы используем приближение математического ожидания средним значением. Т.е. мы имеем некоторый набор $\{\xi_j | j=1,…,P\}$ и оцениваем математическое ожидание как:

\[E_P = \frac 1 P \sum_{j=1}^P \xi_j ,\]

Поскольку хранить все уже полученные награды для каждой ручки, и пересчитывать каждый раз среднее, несколько накладно, мы в нашем алгоритме применяем следующую формулу:

\[E_{P+1} = \frac 1 {P+1} \sum_{j=1}^{P+1} \xi_j = \frac 1 {P+1} \sum_{j=1}^P \xi_j + \frac 1 {P+1} \xi_{P+1}=\] \[= \frac P {P+1} E_P + \frac 1 {P+1} \xi_{P+1} = E_P + \frac 1 {P+1} (\xi_{P+1} - E_P)\]

Иначе говоря мы считаем ошибку $\delta_{P+1}$ между значением величины, полученной на $P+1$-ом шаге и текущим приближением $E_P$ и новое приближение высчитываем как:

\[E_{P+1} = E_P + \frac {\delta_P} {P+1}\]

Обобщая, мы можем записать это в виде:

\[E_{P+1} = \alpha_P \cdot E_P + \beta_P \cdot \delta_P\]

Пока мы использовали $\{\alpha_j=1 | j = 1,2,…\}, \{\beta_j = \frac 1 j | j=1,2,… \}$. Теперь у нас открывается широкое поле возможностей, для экспериментов с тем как должны выглядеть ряды $\{\alpha_j\}, \{\beta_j\}$.

Меняя ряды коэффициентов, можно учитывать различные особенности распределений случайных величин наград. Например, это обобщение представляет практический интерес, когда распределения генерирующие награду меняются со временем. Считать просто среднее значение, при таких условиях уже достаточно глупо и поэтому есть смысл подобрать другие последовательности коэффициентов.

Например, выбрав некоторое $0 < \alpha \le 1$ и задавая $\{\alpha_j=\alpha\}, \{\beta_j = 1 - \alpha\}$, мы получим формулу:

\[E_{P+1} = \alpha E_P + (1-\alpha) (\xi_{P+1} - E_P)\]

известную под названием экспоненциально взвешенное скользящее среднее (или exponentially weighted moving average). Использование такой формулы для оценки, значительно лучше работает для нестационарных распределений, за счет того, что не уменьшает со временем влияния ошибки на последнем шаге.

Это далеко не единственный подход, применимый для случая когда со временем распределения “съезжают” (тех же различных скользящих средних придумано достаточное количество).

“Оптимистичная” инициализация

Вернемся к неменяющимся со временем распределениям и к жадной стратегии без exploration (т.е. $\epsilon = 0$). В алгоритме жадной стратегии мы инициализируем начальные оценки математических ожиданий нулями. В нашем примере с двуруким бандитом, понятно, что начальная инициализация очень важна. Напомню:

Пример.

Пусть у нас есть “двурукий” бандит. Первая ручка всегда выдаёт награду равную 1, вторая всегда выдаёт 2. Действуя согласно жадной стратегии мы дёрнем в начале первую ручку (поскольку в начале у нас оценка математических ожиданий одинаковые и равны нулю) повысим её оценку до $Q_1 = 1$. И в дальнейшем всегда будем выбирать первую ручку, а значит на каждом шаге будем получать на 1 меньше, чем могли бы.

Для данного случая есть как минимум две стратегии, которые приведут к оптимальному решению.

1. На первых $N$ ходах мы дергаем последовательно за каждую из $N$ ручек

2. Проинициализируем начальные оценки математических ожиданий величинами заведомо большими, чем те, что могут выдать ручки

Первая стратегия простая и понятная: дернули по разу каждую ручку и выбрали ту, что даёт наибольшую награду. Так же понятно, что в случае, если награда от ручки случайная величина, данная стратегия хоть и может несколько улучшить ситуацию, но явно не кардинально.

Вторая стратегия предполагает примерно тоже самое, что и первая, но не напрямую. Действительно, проинициализируем начальные значения средних, величинами большими нуля, например, $\{Q_a = 10 | a=1,…,N\}$. Дергаем за первую ручку получаем награду 1, усредняем с 10, получаем оценку на первой ручке 5.5. Следующий шаг: дергаем за вторую ручку получаем награду 2, усредняем - 6. Снова вторая ручка, после усреднения оценки математических ожиданий: 5.5, 4. Ну и так далее. Не то чтобы очень хорошо, за первую ручку мы дернем достаточное количество раз (чем больше начальная инициализация отстает от среднего, тем больше понадобится шагов для того, чтобы сойтись к правильному значению). Зато исследования происходят как бы сами собой.

Попробуем применить, такое изменение инициализации для эксперимента описанного в первой части. Сравним три графика (смотрим только первые 100 шагов). Когда мы инициализируем начальные значения: нулями, -10, 10.

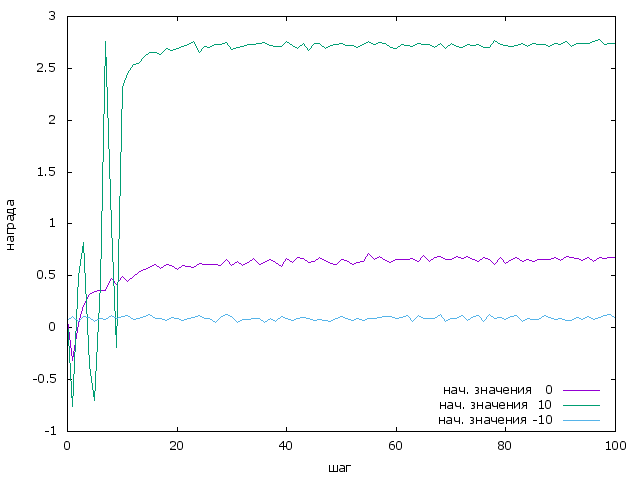
Очевидно, вариант с “оптимистичной” иницилизацией существенно превосходит обычную жадную стратегию.

Сравним теперь этот новый подход с $\epsilon$-жадной стратегией. Лучший результат у нас был при $\epsilon=0.05$. Смотрим график:

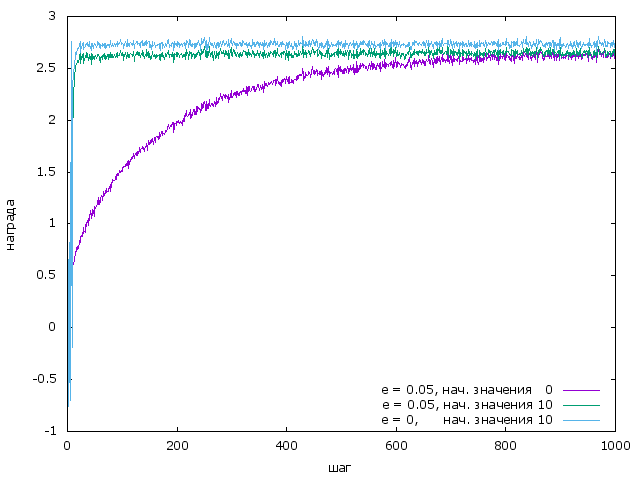
Из графика видно, что простая жадная стратегия с “оптимистичной” инициализацией работает лучше, $\epsilon$-жадной даже если для $\epsilon$-жадной также использовать “оптимистичную” инициализацию. Это объяснимо, ведь фактически в этом случае $\epsilon$-жадная стратегия примерно каждые $1 / \epsilon$ шагов выбирает не оптимальную ручку.

Код можно найти здесь.

---

Литература:

• Sutton and Barto. An introduction to Reinforcement Learning.