arXiv:1708.02002

Авторы статьи решают проблему разбалансировки классов в задаче детектирования объектов (обычно, у нас переизбыток негативов), предлагая заменить поиск сложных негативов и подсчет ошибки только на них, на специфичную штрафную функцию.

Задача детектирования объектов сейчас решается двумя способами. Оба предполагают использование свёрточных нейронных сетей.

Первый способ это двухэтапное детектирование, например, Faster-RCNN. Вначале берется какой-то детектор, который может сносно выбрать прямоугольник с объектом, а затем изображение из этого прямоугольника прогоняется через классификатор. Классификатор кроме основных классов знает еще про класс “негатив” и таким образом отбрасывает лишних претендентов.

Второй способ это работа в один этап, например, YOLO или SSD. Здесь набор претендентов фиксированный (и их обычно достаточно много - тысячи или десятки тысяч), и сетка для каждого даёт ответ о классе, причем опять же возможен негативный ответ.

Второй способ существенно быстрее первого, но уступает по качеству детектирования. Авторы статьи считают, что главная проблема заключается в серьезном перекосе между позитивами и негативами, а именно, для изображения генерируется большое количество претендентов (порядка десятков тысяч), но реальными объектами оказываются единицы. Такой перекос приводит к двум отрицательным эффектам:

1. неэффктивность тренировки, так как большинство претендентов - простые негативы, которые не выдают полезного обучающего сигнала.

2. не смотря на свою простоту (а, следовательно, малый штраф на каждом претенденте) в силу большого количества, эти простые негативы могут перекрыть полезный сигнал и привести к вырождению весов сети.

Обычно с этой проблемой борятся при помощи поиска сложных негативов (hard negative mining), т.е. считают функцию штрафа только на претендентах для которых классификатор выставил высокую вероятность принадлежности какому-то “настоящему” классу. Например, в SSD все претенденты не содержащие объекта вначале выстраиваются в порядке убывания уверенности и затем забираются в соотношении 3 негатива на один позитив.

Авторы, однако, предлагают вместо специфичного алгоритма тренировки, поправить штрафную функцию таким образом, чтобы учесть слабые негативы и погасить их влияние за счёт массовости. Т.е. штрафная функция будет вычисляться на всех претендентах, но такая чтобы большое количество простых негативов не мешало обучению.

Авторы отмечают, что обычно при создании штрафной функции стоит обратная задача - избавиться от outliers, т.е. выбросов. В качестве примера, штрафной функции, которая борется с выбросами приводят функцию Хубера. В статье же решается обратная задача подавить влияние inliers(т.е. простых примеров), чтобы они своей массовостью не отвлекали внимания сети от разбора сложных претендентов.

Focal Loss

Для простоты рассмотрим вначале бинарный классификатор, и кроссэнтропию в качестве функции ошибки. Т.е. каждому элементу у нас приписана одна из двух меток класса $y \in \{\pm 1\}$, а бинарный классификатор выдаёт нам вероятность $p$, что элемент принадлежит классу $y=1$, соответственно, $1 - p$, что классу $y = -1$. Тогда кроссэнтропия:

\[CE(p, y) = \begin{cases} -\log(p), & y = 1\\ -\log(1-p), & y = -1 \end{cases}\]

Обозначаем:

\[p_y = \begin{cases} p, & y = 1\\ 1-p, & y = -1 \end{cases}\]

и тогда можно переписать $CE(p, y) = CE(p_y) = -\log(p_y)$. Логарифм даже при $p_y \gg 0.5$ выдаёт достаточно большие значения, т.е. даже простые примеры, с которыми бинарный классификатор легко справляется, дадут вклад в результирующий штраф и если таких примеров достаточно много, то они просто забьют полезный для обучения сигнал.

Если разбалансировка связана с тем, что представителей одного класса существенно больше чем представителей другого (в нашем случае негативов на несколько порядков больше реальных объектов), то простейший способ побороть проблему - ввести весовой коэффициент. Т.е. давайте возьмем некоторую $\alpha \in [0, 1]$ для класса $+1$ и $1 - \alpha$ для класса $-1$ обозначим:

\[\alpha_y = \begin{cases} \alpha, & y = 1\\ 1-\alpha, & y = -1 \end{cases}\]

и вместо простой кроссэнтропии будем использовать $\alpha$ сбалансированную кроссэнтропию:

\[CE_{\alpha}(p_y) = -\alpha_y \log(p_y)\]

В качестве $\alpha$ можно брать обратную частоту представителей класса в общем наборе, или подбирать его как гиперпараметр обучения.

К сожалению, такая $\alpha$ сбалансированная кроссэнтропия не помогает бороться с простыми примерами (она пенализирует все примеры из класса с большим объёмом, не разделяя слабые от сильных). Авторы предлагают вариант штрафной функции, которая будет понижать влияние именно слабых примеров, т.е. тех для которых классификатор правильно определяет класс с высокой уверенностью ($p \approx 1$). Чтобы это сделать вместо фиксированного коэффициента надо умножать логарифм на что-то функционально зависящее от вероятности, авторы предлагают:

\[FL(p_y) = - (1 - p_y)^{\gamma}\log(p_y), \; \gamma \ge 0\]

Графики этой штрафной функции в сравнении с обычной кроссэнтропией ($\gamma = 0$):

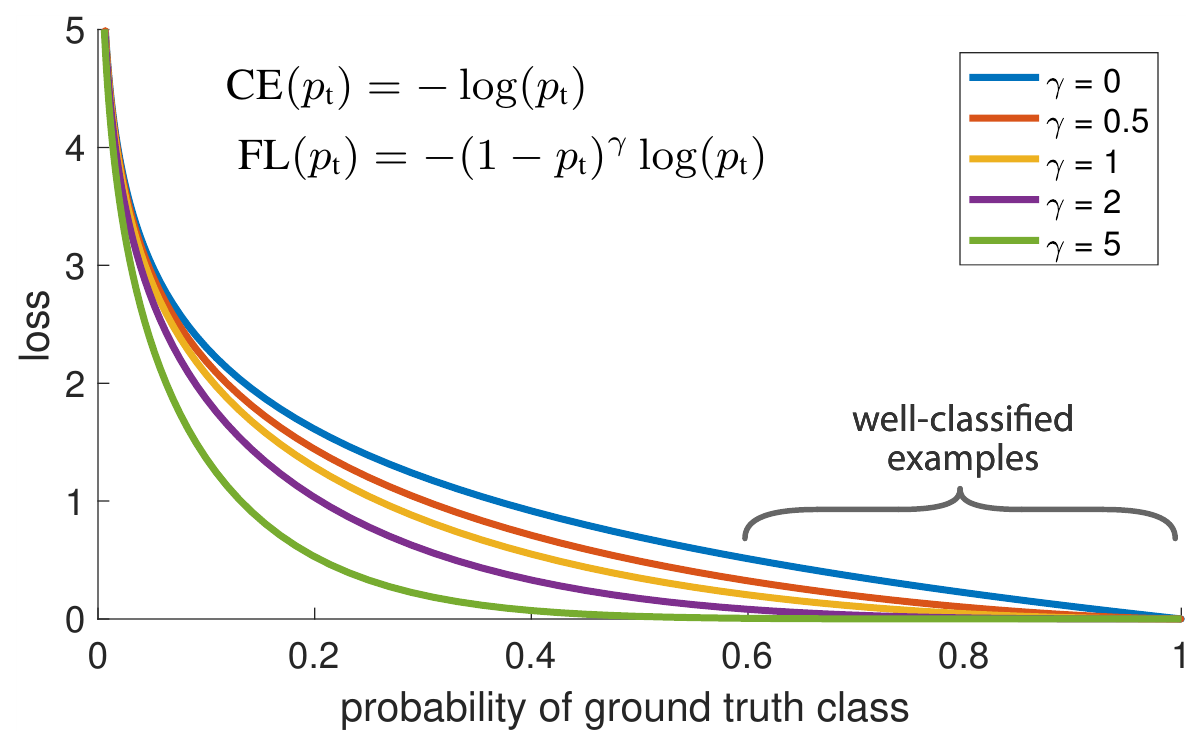
Такая функция обладает двумя полезными свойствами:

1. Если пример не правильно классифицирован и $p_y$ мала, то $(1 - p_y)^{\gamma} \approx 1$ и значит штраф практически не изменяется. В случае, если $p_y \rightarrow 1$, то множитель стремится к нулю и штраф от правильно классифицированного объекта уменьшается.

2. $\gamma$ позволяет гладко понижать вес простых примеров в штрафе.

Авторы на основе экспериментов выбрали $\gamma = 2$. При этом авторы считают правильным оставить и $\alpha$ балансировку, т.е. окончательный вариант штрафной функции будет выглядеть так:

\[FL(p_y) = - \alpha_y(1-p_y)^{\gamma}\log(p_y)\]

Таким образом, эту штрафную функцию можно использовать уже без дополнительных процедур поиска сложных негативов и т.п.

Вторую половину статьи авторы описывают свою сеть - RetinaNet, но это уже не так интересно. Сеть похожа на SSD, только используется FPN подход из более ранней статьи тех же авторов. В результате тренировок с использованием новой штрафной функции, на COCO датасете авторы получают качество лучше чем не только одноэтапные детекторы (SSD, YOLOv2), но и двухэтапного Faster-RCNN.