arXiv:1911.06217

Прошлый раз разбирались с алгоритмом node2vec и тренировкой функции, чтобы вкладывать вершины графа в векторное пространство, для переноса свойств вершин или поиска скрытых связей. В статье, которую хочется разобрать сегодня, авторы используют node2vec для работы с графом представляющим из себя дорожную сеть, а если более точно дорожную сеть Дании. Авторы вкладывают ее в векторное пространство особенностей алгоритмом node2vec и пытаются провесить скоростные ограничения и типы дорог с известных участков на неизвестные.

Сразу отметим, что если до этого мы говорили о вершинах графа, то теперь речь идёт о ребрах, т.е. нам надо будет найти представление для ребер графа.

К счастью, решается это достаточно просто. Если у нас есть граф $\mathcal G = (\mathcal V, \mathcal E)$ и функция $f : \mathcal V \rightarrow \mathbb{R}^d$ отображающая вершины графы в некоторое $d$-мерное векторное пространство особенностей, то для рёбер можно использовать функцию, которая просто берёт и склеивает два вектора, один для вершины из которой выходит ребро, а второй для вершины в которую ребро направлено. Т.е. $g : \mathcal E \rightarrow \mathbb{R}^{2\cdot d}$ для ребра $e = (v_1, v_2)$ будет определена как $g(e) = (f(v_1), f(v_2))$.

Вкладываем вершины в векторное пространство ровно так как это делалось в node2vec. Т.е. ищем такую фуункцию $f$, которая максимизирует сумму:

напомним, здесь $\Omega$ набор обходов, по $r$ штук из каждой вершины, т.е. $|\Omega| = |\mathcal V| \cdot r$, обход это упорядоченный набор вершин: $W =\{v_1, …, v_l\}$, таких что между двумя последовательными вершинами $v_{i-1}$ и $v_i$ есть ребро, выходящее из $v_{i-1}$ и приходящее в $v_i$. Алгоритм добавление вершин в обход как раз основной результат работы про node2vec. $N(W, v_i)$ - окрестность вершины $v_i$, полученная из обхода $W$, размер окрестности определяется параметром $c$, а именно $N(W, v_i) = \{v_{i-c}, …, v_{i-1}, v_{i+1}, …, v_{i+c}\}$.

Датасет

Датасет это выдернутая из OSM датская дорожная сеть. Дорожная сеть представлена в виде ориентированного графа, вершины - точки пересечения дорог или конец дороги, а рёбра, соответственно, связи между этими точками. Ребра ориентированы, потому что очевидно существуют односторонние дороги. Таким образом авторы собрали граф с 583’816 вершинами и 1’291’168 рёбрами. Каждое ребро было размечено одной из 9 категорий дороги (насколько я понял, авторы использовали дополнительные данные, чтобы разметить все рёбра). Также для 163’043 ребра были размечены ограничения скорости. Т.е. во-первых, ограничения скорости были всего у ~12.5 % рёбер, во-вторых, авторы отмечают, что разметка не была равномерна распределена географически, центральные города были размечены лучше. Распределение по классам выглядит следующим образом:

Категории дорог

Класс                    |  Груп. экв. |   Кол-во / Процент  |
--------------------------------------------------------------
Residental               |       90.4% |     570'820 (44.2%) |
Sevice                   |       72.7% |     278'985 (21.6%) |
Unclassified             |       78.0% |     257'725 (20.0%) |
Tertiary                 |       70.2% |     103'830 (8.04%) |
Secondary                |       70.6% |      52'021 (4.03%) |
Primary                  |       71.7% |      22'255 (1.72%) |
Motorway                 |       78.2% |       2'236 (0.17%) |
Motorway Approach/Exit   |       36.8% |       1'749 (0.14%) |
Trunk                    |       81.7% |       1'546 (0.12%) |
--------------------------------------------------------------
Среднее/Итого            |       72.3% |   1'291'168 (100%)  |

Скоростные ограничения

Класс                    |  Груп. экв. |  Кол-во / Процент  |
--------------------------------------------------------------
 50                      |       82.2% |     85'377 (52.4%) |
 80                      |       73.1% |     37'750 (23.2%) |
 40                      |       79.7% |     11'830 (7.26%) |
 60                      |       64.9% |     10'112 (6.20%) |
 30                      |       78.4% |      9'093 (4.03%) |
 70                      |       63.2% |      4'481 (2.75%) |
 20                      |       80.7% |      1'383 (0.85%) |
 110                     |       70.5% |      1'103 (0.68%) |
 90                      |       72.9% |      1'087 (0.66%) |
 130                     |       71.5% |        827 (0.51%) |
--------------------------------------------------------------
Среднее/Итого            |       75.8% |    163'043 (100%)  |

Разберёмся, что такое групповая эквивалентность и зачем она считается. В node2vec мы уже разбирали, что хорошая функция генерации особенностей, должна уметь выделять для вершин (рёбер) групповую и структурную эквивалентность, групповая эквивалентность (homophily - термин, который используется для обозначения этого свойства, я честно поискал перевод - не нашел, много есть про гемофилию - болезнь такая, чтобы не путаться я решил что групповая эквивалентность вполне нормальная замена) - это одинаковые атрибуты сильно связных вершин, а структурная - это когда вершины выполняют одни и теже структурные функции, например, обе являются центром кластера. Для рёбер, в качестве примера, структурной эквивалентности можно привести случай, когда в графе есть несколько сильносвязных внутри кластеров, которые между собой соеденены “мостами”, т.е. единичными рёбрами, вот такие рёбра-мосты можно считать структурно эквивалентными.Авторы вводят формальную метрику групповой эквивалентности рёбер относительно некоторого, приписываемого им атрибута $a$ следующим образом. Пусть есть два смежных ребра $e_1 = (u, v)$ и $e_2 = (v, w)$ графа $\mathcal G = (\mathcal V, \mathcal E)$, назовем групповой эквивалентностью относительно атрибута $a$ - условную вероятность того, что атрибут $a$ приписан ребру $e_1$, если он приписан ребру $e_2$, т.е.

здесь $Z$ - нормирующая константа, а $A(u, v)$ значение атрибута $A$ для ребра $(u,v)$, например, значение ограничения скорости на ребре.

Таким образом вводится числовая оценка для групповой эквивалентности по некоторому конкретному значению атрибута (например, скоростному ограничению 50 кмч). Если атрибут имеет несколько возможных значений $A = \{a_1, …, a_m\}$ мы можем подсчитать оценку для каждого из значений, а дополнительно ещё и взвешенное среднее по всем значениям, которое авторы называют групповой эквивалентностью относительно атрибута $A$:

В таблицах выше можно увидить, что групповая эквивалентность относительно категории дорог на рассматриваемом датасете будет $H^L_{\mathcal G} = 72.3\%$, а относительно скоростных ограничений $H^L_{\mathcal G} = 75.8\%$. Причем для категорий дорог сильно выделяется групповая эквивалентность для Motorway Approach/Exit равная всего $36.8\%$ (что логично, если задуматься о том, что это за категория).

Эксперименты

Вначале применяется node2vec алгоритм и дорожный граф вкладывается в векторное пространство. Делается по $r = 10$ случайных обходов длины $l = 80$ из каждой вершины. Чтобы получить вектор особенностей для ребра, как и писалось выше, соединяются координаты вектора для начальной вершины и для конечной. На полученных особенностях тренируются классификаторы. И для категорий дорог и для скоростных ограничений, исходный датасет разбивается пополам случайным образом, половина элементов уходит в тренировочную, а вторая половина в тестовую часть. И для категорий дорог и для скоростных ограничений авторы тренируют по два классификатора: линейный (логистичесская регрессия “один против всех”) и нелинейный (случайный лес с 10-ю решающими деревьями). Для сравнения, в качестве некоторого базового уровня, предлагается два тривиальных классификатора:

1. Наиболее частый (“Most Frequent”) - этот классификатор всегда приписывает наиболее часто встречающийся класс в датасете.

2. Эмпирическое сэмплирование (“Empirical Sampling”) - приписываем класс случайным образом, с вероятностью распределения равной частотности классов в датасете.

В качестве метрики авторы использую $F_1$ оценку (гармоническое среднее точности и полноты).

Выбор классификатора

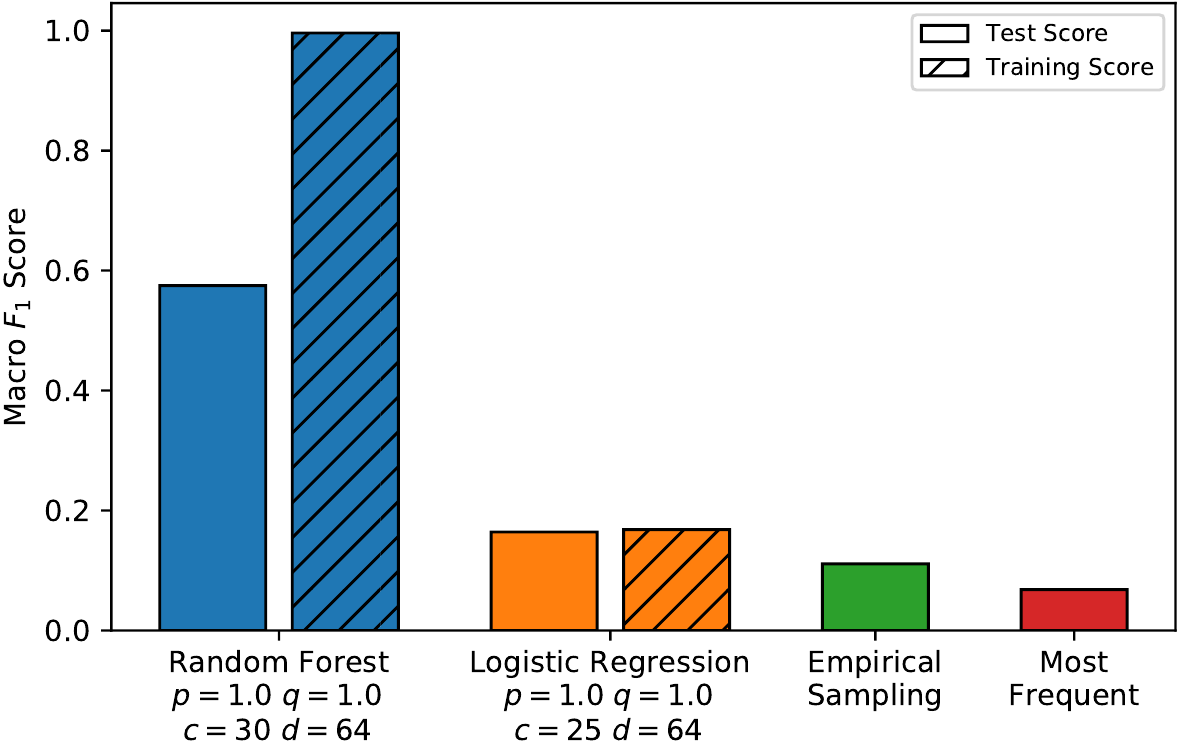
Вначале, авторы берут параметры алгоритма node2vec: $p = 1.0$, $q = 1.0$, $c = 30$, $d = 64$ и смотрят на результаты классификаторов:

Категории дорог

Ограничения скорости

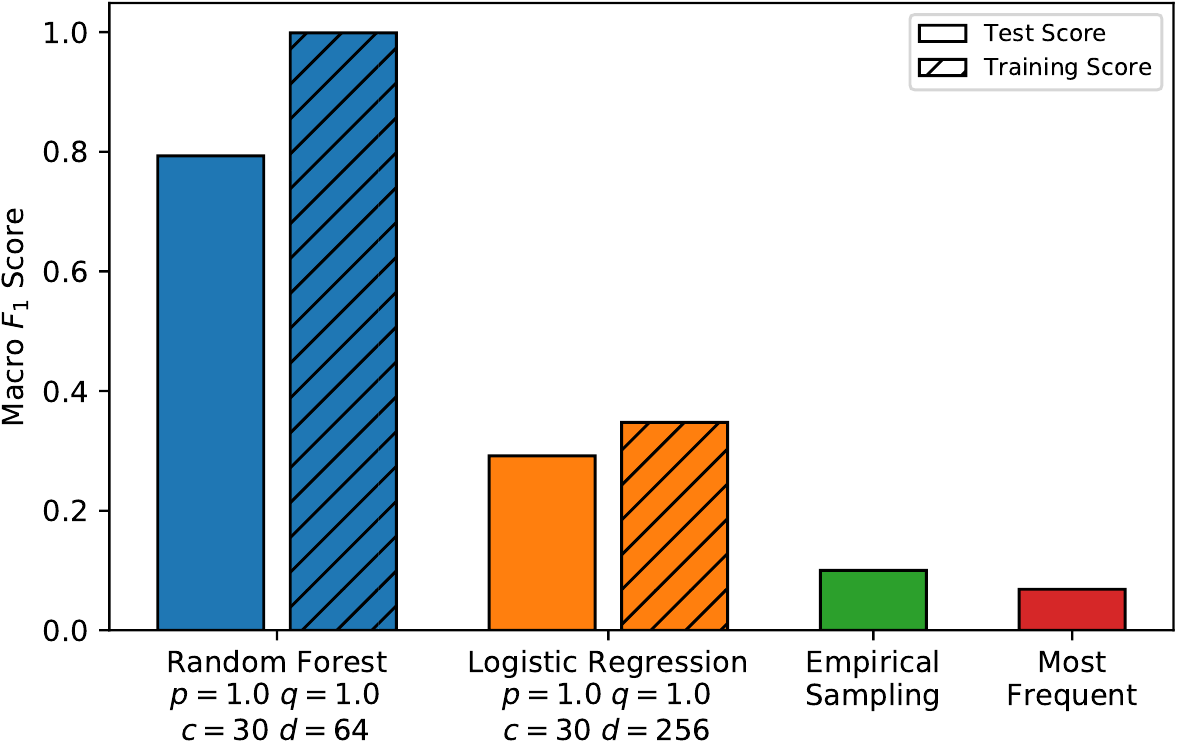
Из графиков очевидно, что логистическая регрессия работает плохо и в первом и во втором случае. Для задачи классификации категорий дорог, она даёт практически такой же результат, как если бы мы присваивали класс просто исходя их частоты представителей этого класса в датасете. В задаче определения ограничения скорости качество линейного классификатора чуть лучше, но всё равно недостаточное. С другой стороны random forest показывает значительно лучший результат на обеих задачах, для категорий дорог $F_1$ оценка на тестовом датасете $~57\%$, для ограничений скорости $~79\%$, при этом на тренировочной части качество добирается практически до $100\%$, а значит скорее всего произошло переобучение, и если уточнить гиперпараметры, то можно будет повысить результат на тестовой части.

Авторы проводят дополнительные эксперименты по линейной сепарабельности классов в пространстве особенностей, но удовлетворительного качества классификации линейным классификатором им добиться не удаётся.

Параметры обходов

Как было описано в исходной статье о node2vec, параметры $q$ и $p$ генерации обходов позволяют плавно менять тип обхода от DFS (Depth-first sampling или поиск в глубину) до BFS (Breadth-first sampling - поиск в ширину). Когда значения $q$ малы то обход будет скорее соответствовать алгоритму DFS, а когда $q$ растёт, то стратегия меняется в сторону похожести на BFS. Параметр $p$ отвечает за повторное посещение вершины в которой уже были, чем $p$ меньше тем выше вероятность вернуться в только что посещенную вершину.

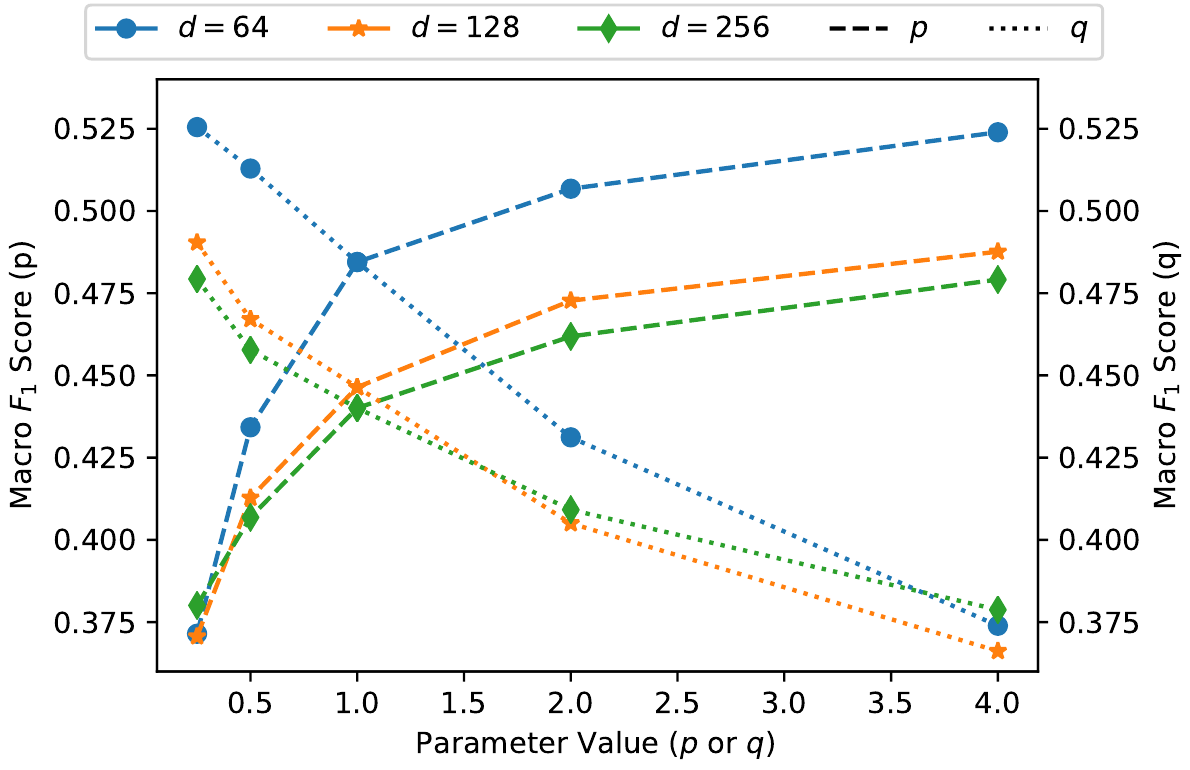
На самом деле все эти тонкости играют скорее философскую роль в процессе, а практически авторы выбирают три различных $d \in \{64, 128, 256\}$ - размерность векторного пространства особенностей и прогоняют процесс для различных $p$ и $q$ оценивая качество получаемого классификатора:

Категории дорог

Ограничения скорости

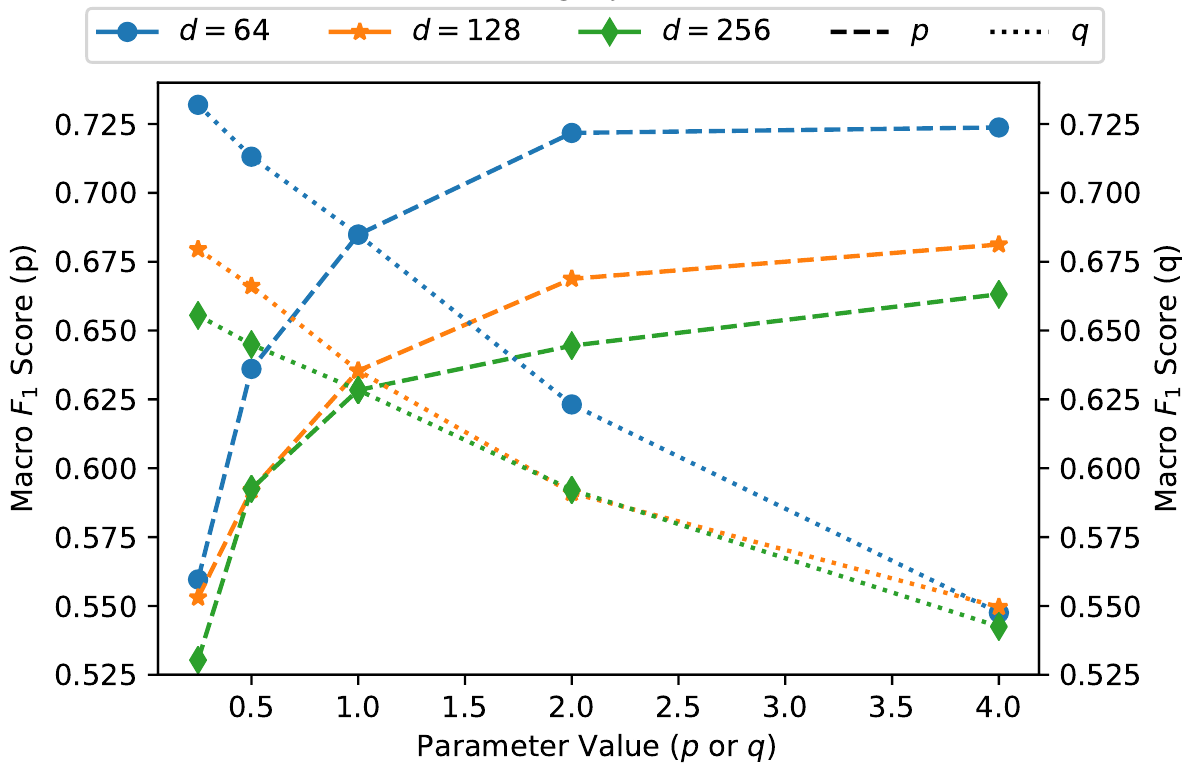
Очевидно качество растёт, при увеличении значения $p$, т.е. когда при обходе мы не возвращаемся в только что посещённую вершину, иначе говоря, с увеличением вероятности исследовать много разных вершин при каждом обходе. Для $q$ наоборот, чем $q$ меньше, тем выше качество, т.е. снова более длинные обходы с захватом разных вершин приводят к улучшению качества классификации.

Еще один эксперимент это изменение качества классификации в зависимости от величины отношения $p / q$ - не вполне понятно, правда, каких неожиданных результатов тут хотели добиться авторы, но график подтверждает только что сделанные выводы: для улучшения качества классификации $p$ надо увеличивать, а $q$ уменьшать, ну и понятно их отношение тоже желательно растить.

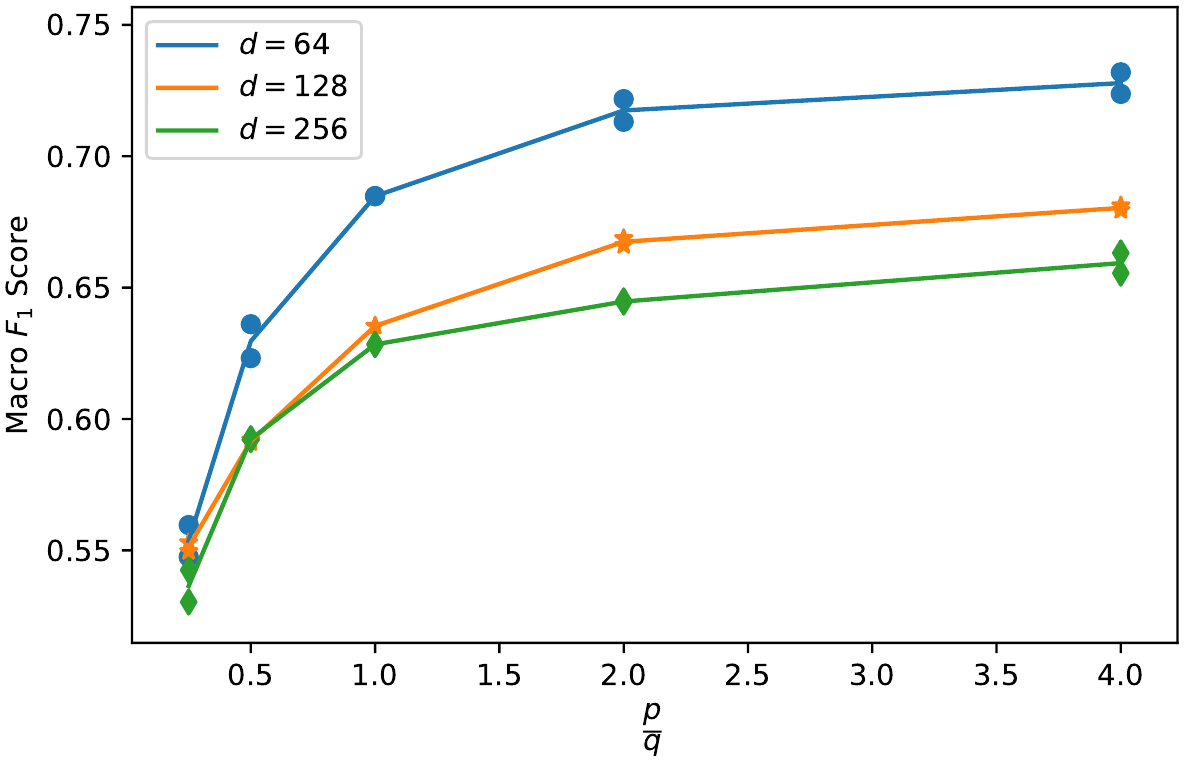
Поскольку одно и тоже отношение можно получить, выбирая разные пары $p$ и $q$ (например, и $p=1$, $q=0.25$ и $p=4$, $q=1$ выдадут нам $p/q = 4$), то на графике показаны среднии от $F_1$ оценок, для одинаковых отношений.

Последний, пока еще незадействованный параметр, это размер окрестности: $c$, как уже не сложно догадаться качество растёт, когда он увеличивается, авторы проверили значения до $30$, уже на $c=15$ рост замедлился, а к $c=30$ практически остановился.

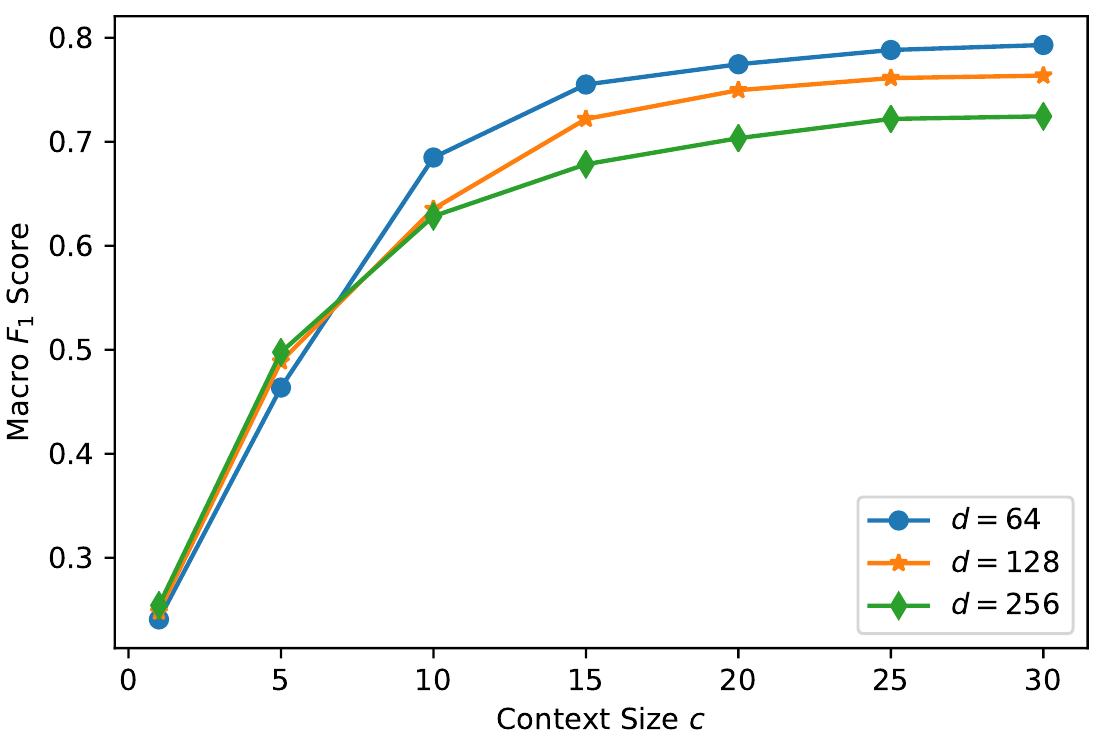
Последнее, что хочется отметить завершая эту часть. Качество получается практически всегда лучше для $d = 64$, чем для $d = 128, 256$.

Связь качества классификации с групповой эквивалентностью

Авторы отмечают, что групповая эквивалентность для ограничения скорости в среднем выше, чем для категорий дорог и более равномерно распределена. Подсчитав оценку качества для каждого класса категорий дорог отдельно, становится очевидной, высокая степень зависимости между оценкой групповой эквивалентности для класса и качества классификации на этом классе.

Класс                    |  Груп. экв. |   F1 качество |
--------------------------------------------------------
Residental               |       90.4% |          0.83 |
Trunk                    |       81.7% |          0.67 |
Motorway                 |       78.2% |          0.62 |
Unclassified             |       78.0% |          0.62 |
Sevice                   |       72.7% |          0.56 |
Primary                  |       71.7% |          0.57 |
Secondary                |       70.6% |          0.54 |
Tertiary                 |       70.2% |          0.52 |
Motorway Approach/Exit   |       36.8% |          0.25 |
--------------------------------------------------------

Вывод

Таким образом, судя по результатам, полученным в статье на дорожном графе хорошо будут решаться задачи классификации в случае, если классы имеют высокую оценку групповой эквивалентности, причем классы с высокой групповой эквивалентностью и классифицироваться будут лучше.

Я тут правда слегка запутался. Авторы говорят, что они добрали $79\%$ качества на ограничениях скоростей, используя random forest классификатор и набор параметров $p = 1.0$, $q = 1.0$, $c = 30$, $d = 64$, потом они показывают как растёт качество от изменения параметров, но как-то итогового результата вида: “и вот наконец мы собрали все полученные знания в кучу, выставили вот такие параметры, натренировали классификатор и получили качество F > 79%” в статье так и не появилось. Это крайне странно и не понятно, возможно я чего-то недопонял.