arXiv:1905.03561

Продолжаем тему поиска особых точек и их дескрипторов при помощи нейронных сетей. В прошлый раз разбирали статью, где использовалась сетка с “двумя головами”, которая в каком-то смысле повторяла классический подход, одна голова искала особые точки, а вторая потом для этих особых точек выдавала дескрипторы (на самом деле дексрипторы были для всех точек изображения, но нас интересовали только те которые нашлись как особые).

Сегодня разберем еще одну статью, про поиск особых точек на картинке нейронными сетями.

В этой статье авторы вполне логично замечают, что при помощи нейронной сети можно сформировать дескрипторы сначала, а уже потом выбрать по этим дескрипторам хорошие особые точки.

Т.е. авторы предлагают заменить “detect-then-describe” подход на “detect-and-describe” и даже приводят красивую картинку.

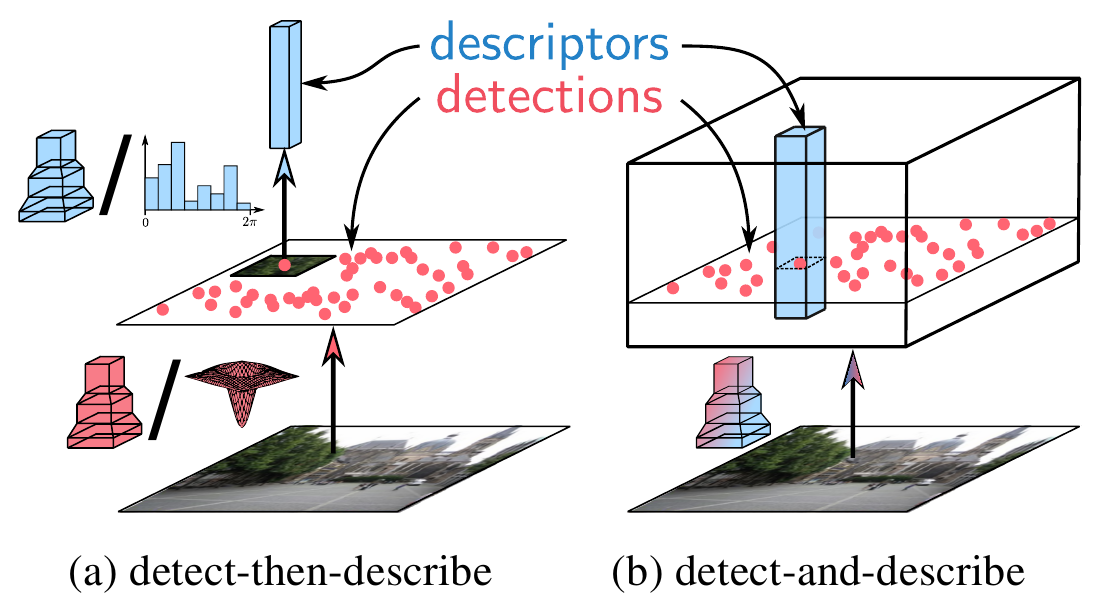
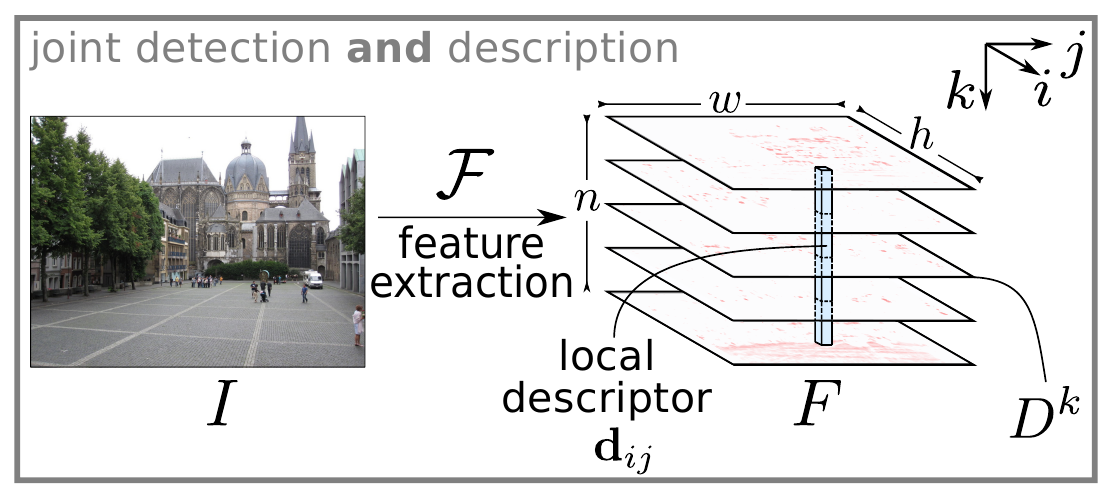
Идея понятная, исходное изображение, при помощи свёрточной сети, преобразуем в тензор особенностей $F \in \mathbb{R}^{h \times w \times n}$, этот тензор авторы предлагают рассмотреть с двух позиций.

Во-первых, как двумерный набор векторов размерности $n$:

\[d_{ij} = F_{ij:} \in \mathbb{R}^n\]

теперь, если нормализовать эти вектора,

\[\hat{d}_{ij} = d_{ij} / \left \| d_{ij} \right \|_2\]

и правильно натренировать сеть, то есть надежда, что для одной 3Д-точки на разных изображениях, эти вектора будут близки в смысле обычного расстояния. Т.е фактически вектора $\hat{d}_{ij}$ выдают нам дескрипторы, и решают половину задачи.

Во-вторых, этот же тензор можно представить как набор плоскостей:

\[D^k = F_{::k} \in \mathbb{R}^{h \times w}, k = 1,...,n\]

Авторы рассматривают эти плоскости $D^k$ как аналоги Difference-of-Gaussian из алгоритма SIFT и предлагают использовать их для детектирования особых точек.

Будем точку $(i, j)$ считать особой, если и только если для $k = \arg \max_t D^t_{ij}$, $D^k_{ij}$ - локальный максимум в $D^k$.

Другими словами для точки $(i,j)$ выбираем лучшую плоскость $D^k$ и потом проверяем является ли эта точка на этой плоскости локальным максимумом.

Таким образом, один тензор $F$, полученный при помощи свёрточной нейронной сети, одновременно решает и проблему детектирования особой точки и проблему формирования для этой точки дескриптора.

Осталось натренировать нужную сеть. Но для тренировки необходимо переформулировать критерий особенности точки, в дифференцируемом виде, чтобы можно было считать градиенты. Авторы ослабляют исходное определение и вводят “мякгое условие детектирование”. Вначале две формулы:

1. Мягкий локальный максимум:

   \[\alpha^k_{ij} = \frac {\exp \left( D^k_{ij} \right)} {\sum_{(i',j')\in\mathcal{N}(i,j)} \exp\left(D^k_{i'j'}\right)}\]

   здесь $\mathcal{N}(i,j)$ - это пиксели квадрата $3 \times 3$ с центром в $(i, j)$.

2. Поканальный non-maximum suppression:

   \[\beta^k_{ij} = \frac {D^k_{ij}} {\max_t D^t_{ij}}\]

Объединяя эти две формулы:

\[\gamma_{ij} = \max_k\left(\alpha^k_{ij} \cdot \beta^k_{ij}\right)\]

вводим мягкую оценку детекции в точке $(i, j)$:

\[s_{ij} = \frac {\gamma_{ij}} {\sum_{(i', j')} \gamma_{i'j'}}\]

В качестве иллюстрации:

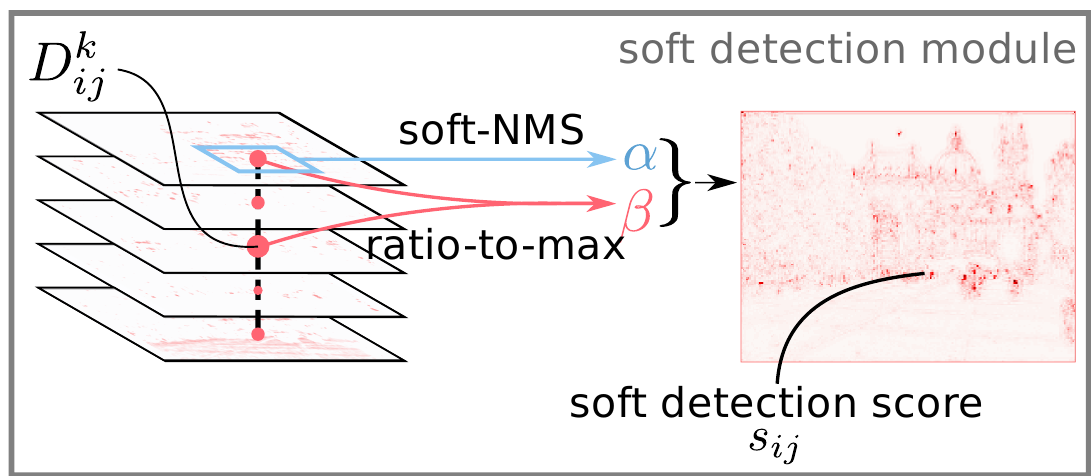
Однако, это пока еще не штрафная функция. В отличии от SuperPoint, в данной статье не идёт речи о синтетических данных или автоматическом расширении датасета. Авторы статьи берут вполне натуральные фотографии, и размечают соответствие точек на парах изображений. В качестве датасета они используют Megadepth Dataset, а парные точки размечают автоматически, используя знания о преобразованиях, связывающих пары изображений, и карту глубины (чтобы исключить точки, которые скрыты на одном из изображений). Таким образом для пары изображений $(I_1, I_2)$ определены связанные точки $A \in I_1$ и $B \in I_2$. Выберем теперь еще по одной точке на каждом изображении $N_1 \in I_1$ и $N_2 \in I_2$, выбирать будем таким образом, чтобы $N_1$ лежала вне окрестности $A$ и аналогично $N_2$ вне окрестности $B$. Авторы предлагают в качестве окрестности точки брать квадрат со стороной $2K,\, K = 4$ в карте особенностей.

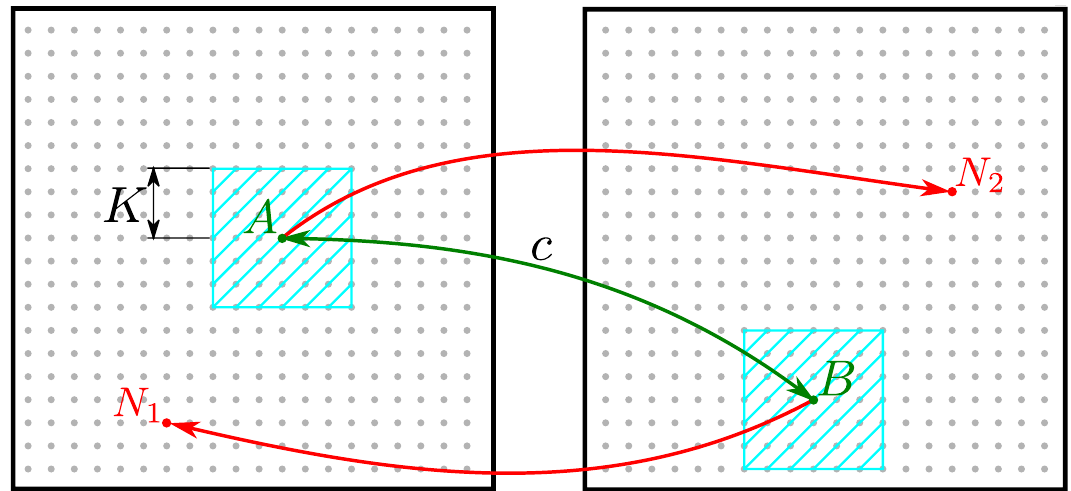
Учитывая, что карту особенностей предполагается брать со слоя conv4_3 сети VGG, а значит каждая точка на карте особенностей, вбирает в себя информацию о квадрате $65 \times 65$ из исходного изображения, то отступив на $K = 4$, мы получим точку, квадрат вокруг которой на исходном изображении пересекается с квадратом точки $A$ ($B$) меньше чем на 50%. Нам нужны hard negatives, поэтому точку $N_1$ выберем с дескриптором максимально “похожим” на дескриптор точки $B$:

\[N_1 = \arg \min_{P \in I_1} \left \| \hat{d}^{(1)}_{P} - \hat{d}^{(2)}_{B} \right \|_2, \, \left\| A - P \right\|_{\infty} > K\]

Аналогично выберем точку $N_2$ с дескриптором “близким” к точке $A$.

Штрафная функция должна расти, во-первых, с ростом расстояния между дескрипторами связанных точек $A$ и $B$, во-вторых, с уменьшением расстояния между дескрипторами несвязанных точек $A$ и $N_2$, $B$ и $N_1$. Обозначим

\[p(A, B) = \left \| \hat{d}^{(1)}_{A} - \hat{d}^{(2)}_{B} \right \|_2\]

и

\[n(A, B) = \min \left( \left \| \hat{d}^{(1)}_{A} - \hat{d}^{(2)}_{N_2} \right \|_2, \left \| \hat{d}^{(1)}_{B} - \hat{d}^{(2)}_{N_1} \right \|_2 \right)\]

Первая функция меряет расстояние между связанными точками, вторая между несвязанными, объединим их:

\[m(A, B) = \max \left(0, M^2 + p^2(A, B) - n^2(A, B) \right)\]

$M$ - здесь гиперпараметр, для отсечения краевых ситуаций. Теперь, если для пары изображений у нас есть набор пар связанных точек $C = \{(A,B) | A\in I_1, B \in I_2\}$, то окончательно штрафная функция запишется в виде суммы по всем таким парам, с учетом оценки детекции, определенной ранее:

\[\mathcal{L}(I_1, I_2) = \sum_{(A,B) \in C} \frac {s^{(1)}_A \cdot s^{(2)}_B} {\sum_{(A', B') \in C} s^{(1)}_{A'} \cdot s^{(2)}_{B'}} \cdot m(A, B)\]

Результаты

Тестировали подход на датасете HPatches. Брали наборы из 6 связанных изображений. 52 набора с изменением освещения, но фиксированной точкой съёмки, и еще 56 наборов с фиксированным освещением, но с изменяющейся точкой съёмки. Для тестов брали первое изображение из набора и матчили из с оставшимися пятью, т.е. получилось $5 \cdot (52 + 56) = 540$ пар.

В качестве численной оценки авторы используют среднюю точность совпадения (mean matching accuracy (MMA)). Т.е. для пары изображений, они находят особые точки и матчат их используя nearest neighbor search, затем отбирают правильно сматченные (поскольку для пары изображений известна гомография это можно сделать), при этом используют порог в пределах которого допускается ошибка репроекции.

Сравнение с другими подходами не сильно поражает воображение:

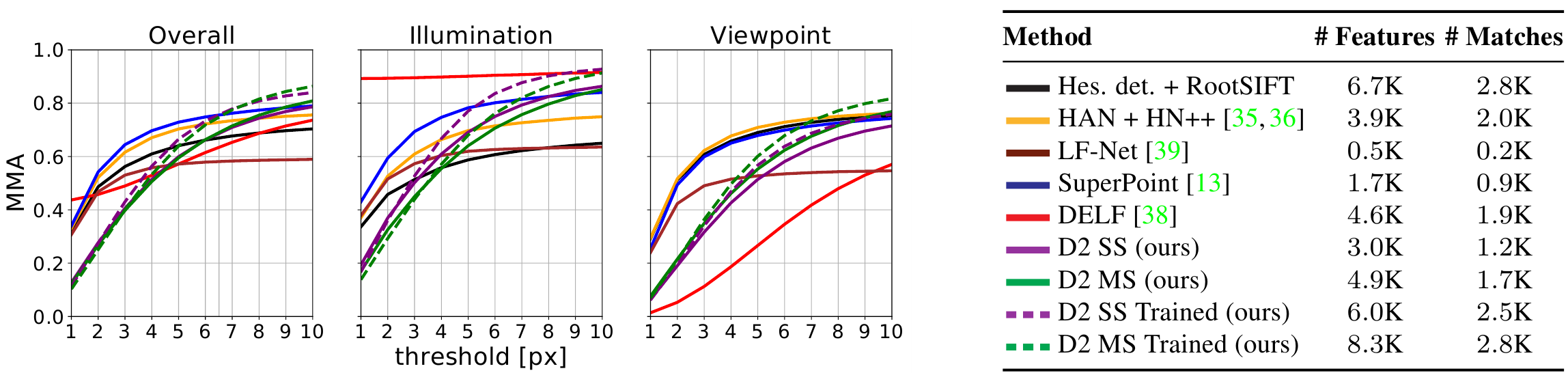
На объедененном датасете качество нового подхода становится лучше других только при пороге приблизительно $6.5$ пикселей. Т.е. с одной стороны много точек и много точек правильно сматченных, но только если критерий “правильности” размыт в достаточно широкую область.

Авторы далее приводят статистику на использование данного подхода в задаче 3D реконструкции. Показал себя близко к уровню RootSIFT, но ошибка репроекции всё таки больше (практически вдвое на всех примерах, которые приведены в статье).

Выводы

Если в SuperPoint был некий задор: синтетический датасет, его расширение. Да, результаты тоже были не то чтобы очень хороши, но подход интересный. То здесь из интересного - штрафная функция, остальное всё достаточно стандартно для алгоритмов с использованием нейронных сетей. Ну и, к сожалению, результаты не перекрывают старые подходы, правда тут не очень понятно то ли это не устранимая проблема, то ли просто не достаточный датасет или параметры тренировки.