arXiv:1609.02907

В статье рассказывается об использовании свёрточной сети на графе для полуавтоматического обучения классификатора.

Задача стоит: взять граф некоторым вершинам которого приписан класс, и продолжить классификацию на неразмеченные вершины. Например, мы хотим классифицировать документы, помещаем их в вершины графа, и связываем две вершины ребром, если один из документов ссылается на другой. При этом у нас только небольшой части документов приписаны метки, а мы хотим разметить все документы.

Итак у нас есть взвешенный неориентированный граф $\mathcal G = (\mathcal V, \mathcal E, W)$, $\mathcal V$ - вершины ($N$ штук), $\mathcal E$ - рёбра и $W \in\mathbb R^{N\times N}$ - матрица весов. Обозначим $\mathcal L = W - D$ - лапласиан графа.

Один из способов решать поставленную выше задачу это опираясь на “гладкость” разметки на графе. Гладкость рассматривается на базе лапласиана (про определение гладкости сигнала на графе с помощью Лапласиана можно посмотреть в статье про графы). Для этого зададим штрафную функцию $L = L_0 + \lambda L_{reg}$ состоящую из взвешенной суммы двух слагаемых. $L_0$ - штрафует за ошибку на размеченных вершинах, а

\[L_{reg} = \sum_{i,j}W_{ij} \left \| f\left(X_i\right) - f\left(X_j\right)\right \|^2 = f\left(X\right)^T \mathcal L f\left(X\right)\]

отвечает за сглаживание разметки. $f(\cdot)$ - некая функция (например, реализованная в виде нейронной сети), которая преобразует вектор особенностей вершины графа.

Проблема такого подхода в том, что рёбра не обязательно кодируют “одинаковость” вершин, они могут содержать какую-то другую информацию.

Поэтому авторы статьи хотят закодировать в нейронной сети, представляющей функцию $f(X, W)$, еще и структуру самого графа. Подбирать эту функцию (тренировать веса) планируется, используя штраф $L_0$ на размеченных вершинах. Предполагая, что натренированная таким образом сеть будет правильно представлять и размеченные и неразмеченные вершины.

Многослойная свёрточная сеть на графе

Обозначим $\tilde W = W + I$ - т.е. добавим петлю для каждой вершины. $\tilde D$ - диагональная матрица степеней вершин на базе $\tilde W$. Аторы статьи предлагают один свёрточный слой на графе представлять в виде преобразования:

\[H^{(l+1)} = \sigma\left(\tilde D^{-\frac 1 2} \tilde W \tilde D^{-\frac 1 2} H^{(l)} A^{(l)}\right)\]

$\sigma(\cdot)$ - нелинейность (например, ${\rm ReLU}$), $H^{(l)} \in \mathbb R^{N \times F}$ - отклик $l$-го слоя на графе ($H^{(0)} = X$ исходные вектора особенностей вершин) и $A^{(l)}$ весовая матрица, которую мы хотим натренировать в результате обучения.

Авторы обосновывают свой подход связью такого свёрточного слоя с операцией свёртки на графе. В качестве лапласиана выбирается нормализованный симметричный вариант: $\mathcal L_{sym}=D^{-1/2} \mathcal L D^{-1/2} = I - D^{-1/2} W D^{-1/2}$ и свёртка сигнала $x$ с фильтром $g$ на графе аппроксимируется при помощи полиномов Чебышева:

\[g \ast_{\mathcal G} x \approx \sum_{k=0}^{K} a_k T_k(\tilde{\mathcal L}_{sym})x\]

здесь

\[\tilde{\mathcal L}_{sym} = \frac 2 {\lambda_{max}} \mathcal L_{sym} - I\]

линейно сдвинутый лапласиан, у которого собственные числа попадают в отрезок $[-1, 1]$ как это требуется, чтобы можно было использовать полиномы Чебышева. $a_k,\,\forall k=0,…,K$ - это те параметры, которые мы планируем тренировать. Напомним, что на результат в вершине $i$ будут влиять значения сигнала в вершинах отстающих от нее не более чем на $K$ рёбер.

Можно сделать многослойную свёрточную сеть на графе, если собирать такие слои друг за другом, вставляя в промежутки нелинейность действующую на сигнал в каждой вершине.

Авторы статьи предлагают ограничиться вариантом с $K=1$, т.е. влиять на результат свёртки в данной вершине будут только значение сигнала в её непосредственных соседях. Однако, собирая последовательно несколько свёрточных слоёв мы, аналогично тому как это происходит для обычных свёрточных сетей, увеличим расстояние до вершин, влияющих на сигнал в данной.

Aвторы предлагают оценить максимальное собственное число лапласиана как $\lambda_{max} \approx 2$. На самом деле для нормализованного симметричного Лапласиана, который используют авторы $\lambda_{max} \le 2$ и равенство достигается только в случае, если граф двудольный (см., например, Lemma 1.7, Chung. “Spectral Graph Theory”), таким образом замена на $2$ в данном случае допустима.

Получаем:

\[\tilde{\mathcal L}_{sym} = \mathcal L_{sym} - I\]

и свёртка запишется в виде:

\[g \ast_{\mathcal G} x \approx a_0 x + a_1 (\tilde{\mathcal L}_{sym} - I) x = a_0 x - a_1 D^{-1/2} W D^{-1/2} x\]

Наконец авторы предлагают упростить данную свёртку положив $a = a_0 = -a_1$. Во-первых, это уменьшит число параметров, а значит и вероятность перетренировать сеть, во-вторых, уменьшит число операций и значит снизит расходы на вычисления. В результате получаем:

\[g \ast_{\mathcal G} x \approx a \left(I + D^{-1/2} W D^{-1/2}\right) x\]

Однако, в таком виде преобразование остаётся численно нестабильным и может привести к проблеме исчезающих/взрывающихся градиентов. Поэтому авторы статьи предлагают заменить $I + D^{-1/2} W D^{-1/2}$ на ренормализованную версию $\tilde D^{-1/2} \tilde W \tilde D^{-1/2}$, где $\tilde W = W + I$, а $\tilde D$ - соответственно диагональная матрица степеней, для матрицы весов $\tilde W$.

Пока это всё было для одномерного сигнала в каждой вершине графа, теперь если взять $X \in \mathbb R^{N \times C}$, т.е. в каждой вершине сигнал будет представлен в виде вектора из $\mathbb R^{C}$, или другими словами каждой вершине приписан вектор особенностей размерности $C$. И мы хотим применить $F$ фильтров, чтобы получить в каждой вершине новый вектор особенностей размерности $F$, или тензор особенностей на графе $Z \in \mathbb R^{N \times F}$, то свёртку можно записать в виде:

\[Z = \tilde D^{-1/2} \tilde W \tilde D^{-1/2} X A\]

здесь $A \in \mathbb R^{C \times F}$ матрица параметров, которые мы будем тренировать. Сложность такой операции будет $O(\vert\mathcal E\vert F C)$.

Пример

В качестве примера, авторы приводят двухслойную сеть на частично размеченном графе. Вначале взяв матрицу весов графа $W$, вычисляется матрица $\hat W = \tilde D^{-1/2} \tilde W \tilde D^{-1/2}$. Затем функция представляется в виде:

\[Z = f(X, W) = {\rm softmax}\left(\hat W \cdot {\rm ReLU}\left(\hat W X A^{(0)} \right) A^{(1)} \right).\]

$A^{(0)} \in \mathbb R^{C\times H}$, $A^{(1)} \in \mathbb R^{H\times F}$, здесь $C$ - размерность векторов особенностей вершин исходного графа, $H$ - размерность векторов отклика на вершинах графа в промежуточном слое, и $F$ - количество классов на которые мы планируем поделить вершины.

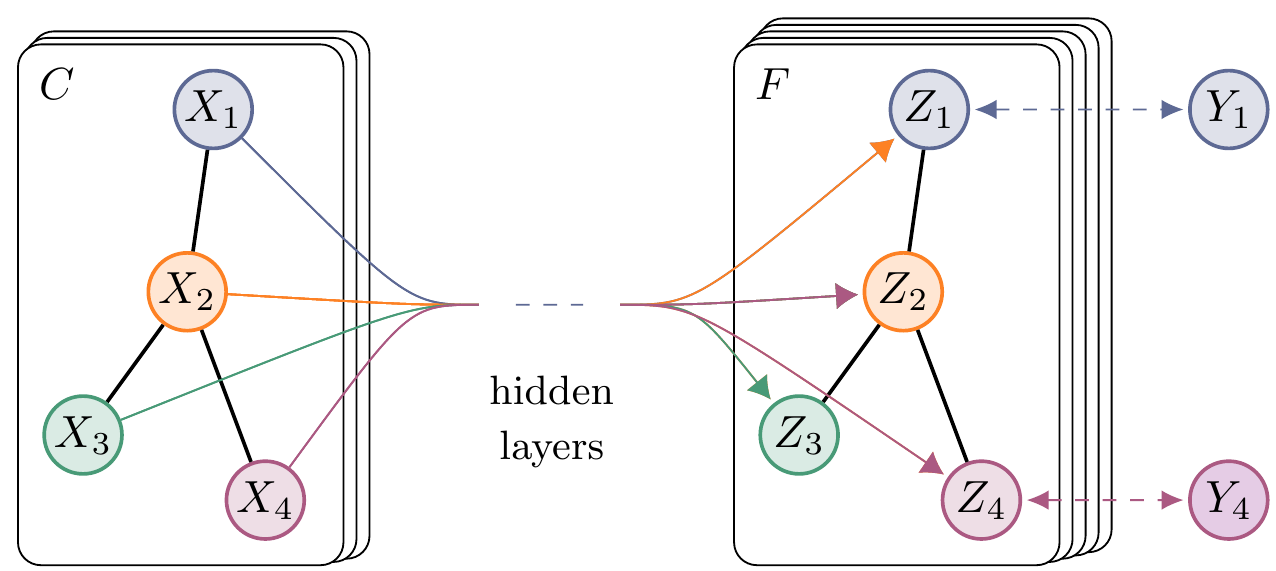
Функцию ошибки авторы статьи предлагают задать в виде кроссэнтропии, на тех вершинах которые имеют разметку ($Y_L$):

\[L = - \sum_{l\in Y_L}\sum_{f=1}^F Y_{lf} \log \left( Z_{lf} \right)\]

Тренировать предлагается обычным градиентным методом, при этом на тех датасетах на которых авторы тестировали сеть, можно было не делить набор на минибатчи, а запускать каждый шаг сразу на всем наборе.

Судя по цифрам, которые приводят авторы, данный подход победил другие, имевшиеся на тот момент, на всех датасетах (три датасета были про разметку статей на классы, и четвертый с базой знаний).

Что надо отметить - в данной статье уже есть свёрточные слои на графе, однако, если сравнивать со свёрточными нейронными сетями применяемыми для картинок, например, то пока нет слоёв аналогичных тем, что осуществляют pooling.