Двойная свёрточная сеть на графе для полуавтоматической классификации
Разбирали статью про полуавтоматическое обучение, в статье описывалась сеть с помошью которой, имея разметку для части вершин графа, можно продолжить эту разметку на непомеченные вершины. В новой статье предлагается улучшить решение этой задачки путём добавления еще одного слагаемого в штрафную функцию. Это слагаемое описывает связь между вершинами графа, основанную на положительной точечной взаимной информации (positive pointwise mutual information) и помогает улучшить глобальную согласованность разметки.
Итак у нас снова есть взвешенный неориентированный граф $\mathcal G = (\mathcal V, \mathcal E, W)$, $\mathcal V$ - вершины ($N$ штук), $\mathcal E$ - рёбра и $W \in\mathbb R^{N\times N}$ - матрица весов этого графа. При этом каждой вершине из множества $Y_L \subset \mathcal V$ приписана метка и мы хотим научиться приписывать метки оставшимся вершинам графа из $\mathcal V \setminus Y_L$.
В предыдущей статье, чтобы продолжить разметку строилась свёрточная сеть на графе, состоящая из нескольких слоёв, которые определялись функцией свёртки:
\[H^{(l+1)} = \sigma\left(\tilde D^{-\frac 1 2} \tilde W \tilde D^{-\frac 1 2} H^{(l)} A^{(l)}\right)\]здесь $\tilde W = W + I$, $\tilde D$ - диагональная матрица степеней вершин на базе $\tilde W$ ($\tilde D_{ii} = \sum_j \tilde W_{ij}$), $\sigma(\cdot)$ - нелинейность (например, ${\rm ReLU}$), $H^{(l)} \in \mathbb R^{N \times F_l}$ - отклик $l$-го слоя на графе ($H^{(0)} = X$ исходные вектора особенностей вершин) и $A^{(l)}$ весовая матрица, которую мы тренируем в процессе обучения.
В качестве последнего слоя добавлялся softmax:
\[Z = {\rm softmax}\left(H^{(T)}\right),\]а штрафная функция выглядела как:
\[L_0 = - \frac 1 {\vert Y_L \vert} \sum_{i\in Y_L}\sum_{f=1}^F Y_{if} \log \left( Z_{if} \right)\]Однако, в силу того как работает преобразование свёртки, разметка вершины, зависела только от локальной структуры графа, что не всегда продуцирует правильный результат. Авторы решили добавить в штрафную функцию регуляризацию, отвечающую за глобальную согласованность на графе.
\[L_{reg} = \frac 1 N \sum_{i=1}^N \left\|Z_{i\,:} - Q_{i\,:}\right\|^2\]$Z_{i\,:}$ - вероятности классов для $i$-ой вершины графа, полученная по исходной свёрточной схеме. А матрица $Q$ должна отвечать за глобальную согласованность и авторы предлагают получать её так же как и $Z$ (т.е. используя несколько свёрточных слоёв на графе с softmax на конце). Только в свёрточных слоях вместо весовой матрицы графа использовать матрицу положительной точечной взаимной информации $P$. Как её получить мы обсудим позже, пока же заметим, что у нас появляется как бы два набора свёрточных слоёв через которые проходят вектора особенностей вершин, первый $\left\{H^{(l)}\right\}$ и второй:
\[J^{(l+1)} = \sigma\left(D_P^{-\frac 1 2} P D_P^{-\frac 1 2} J^{(l)} A^{(l)}\right)\]$D_P$ - диагональная матрица, соответствующая $P$. $Q$ получаем снова используя softmax на последнем свёрточном слое:
\[Q = {\rm softmax}\left(J^{(T)}\right),\]тогда штрафная функция принимает вид:
\[L = L_0 + \lambda(t) L_{reg}\]Важно отметить, что веса свёрточных слоёв $A^{(l)}$ будем тренировать общие и для свёрток на базе матрицы весов и для свёрток на базе матрицы ПТВИ.
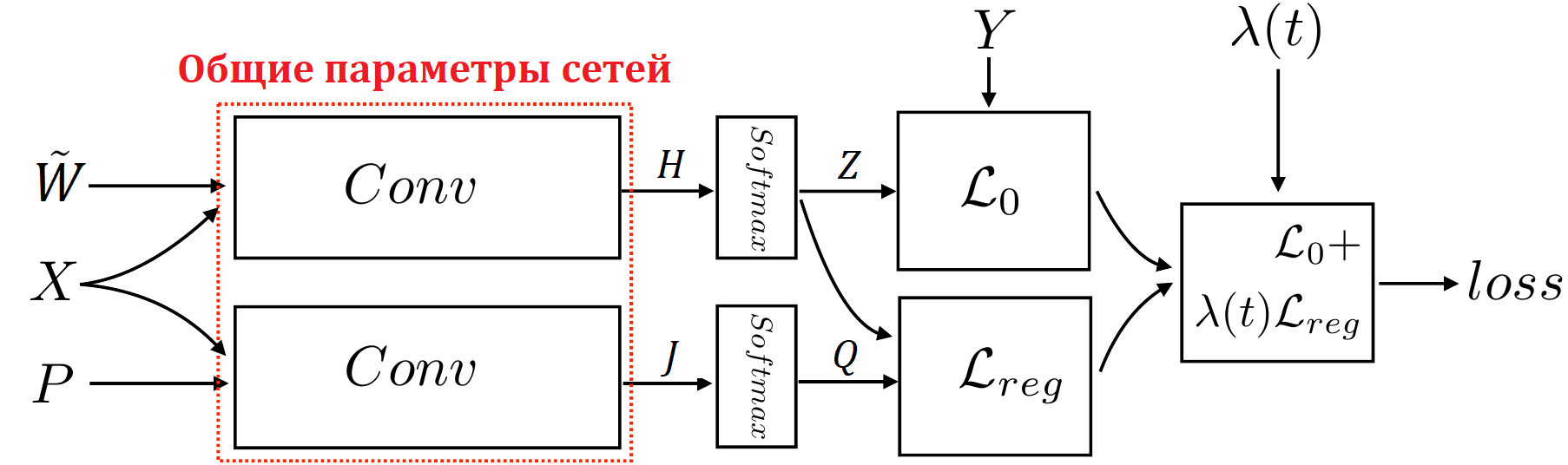
$\lambda(t)$ - предлагается увеличивать со временем тренировки, т.е. вначале мы тренируем сеть практически без дополнительного слагаемого в штрафной функции, а с каждой следующей эпохой увеличиваем влияние именно регуляризации. В статье есть сравнение разных вариантов зависимости $\lambda$ от эпохи и соответствующая точность классификации.
Итак осталось описать процедуру построения матрицы $P$. Вначале вычислим частотную матрицу $F \in \mathbb R^{N\times N}$.
Вход: матрица весов $W$ графа; длина пути $q$; размер окна $w$; количество путей из каждой вершины $\gamma$
Выход: частотная матрица $F$
-
Устанавливаем все элементы матрицы $F$ равными нулю.
-
Для каждой вершины $\mathcal v \in \mathcal V$ графа. Повторяем $\gamma$ раз
2.1. Генерируем случайный путь $S = \left\{\mathcal v_1 = \mathcal v, …, \mathcal v_q \right\}$ длины $q$ из вершины $\mathcal v$ на базе матрицы весов $W$.
2.2. Для каждой пары вершин $(\mathcal v_i, \mathcal v_j)$ из $S$ увеличиваем элементы: $F_{\mathcal v_i \mathcal v_j} += 1,\; F_{\mathcal v_j \mathcal v_i} += 1$
Случайный путь генерируется, используя вероятность перехода на $t+1$-ом шаге из $i$-ой вершины в $j$-ую:
\[\mathbb P(\mathcal v_{t+1} = j \vert \mathcal v_t = i) = W_{ij} / \sum_i W_{ij}\]Вычислив частотную матрицу $F$. Обозначим:
\[\begin{align*} p_{ij} &= \frac {F_{ij}} {\sum_{i,j} F_{ij}}, \\ p_{i*} &= \frac {\sum_j F_{ij}} {\sum_{i,j} F_{ij}}, \\ p_{*j} &= \frac {\sum_i F_{ij}} {\sum_{i,j} F_{ij}}, \end{align*}\]$p_{ij}$ будут приближения совместного распределения появления на пути $i$-ой вершины при выходе из $j$-ой, и соответствующих частотных распределений $p_{i}$, $p_{j}$. Теперь воспользуемся понятием точечной взаимной информации (см. Bouma, Gerlof. “Normalized (Pointwise) Mutual Information in Collocation Extraction”) и определим матрицу $P$ элементы которой зададим формулой:
\[P_{ij} = \max \left\{\ln\left(\frac {p_{ij}} {p_{i*}\cdot p_{*j}}\right), 0\right\}\]отсечение отрицательных элементов приводит к матрице с положительной точечной взаимной информацией. Авторы статьи предполагают, что эта матрица отвечает за глобальную согласованность вершин графа. Во всяком случае их эксперименты показывают улучшение распространения разметки при использовании дополнительных свёрточных слоёв на базе матрицы $P$.
В результате добавления дополнительной ветки в свёрточную сеть и дополнительного регуляризационного члена в штрафную функцию увеличение качества работы составляет от 2% до 8% в зависимости от датасета.
Интересно, что новая сеть DGCN (Dual Graph Convolutional Network) в отличии от обычной GCN лучше работает в условиях слабой исходной разметки. Например, авторы приводят следующую табличку результатов на датасете Simplified NELL:
% Размеченных | 1% | 5% | 10% | 15% | 20% | 25% |
---------------------------------------------------------------
DGCN | 26.0% | 62.6% | 70.4% | 70.6% | 72.0% | 72.8% |
GCN | 20.4% | 53.0% | 63.4% | 64.6% | 68.6% | 69.8% |
---------------------------------------------------------------
Разница | +5.6% | +9.6% | +7.0% | +6.0% | +3.4% | +3.0% |
---------------------------------------------------------------