arXiv:1704.03165

Авторы предлагают новый подход к представлению вершин графа в виде элементов некоторого векторного пространства. При этом вектора, представляющие структурно похожие вершины, близки в смысле обычной метрики векторного пространства.

На самом деле, построение функции, вкладывающей вершины графа в некоторое векторное пространство, неоднократно обсуждалось в различных статьях, например, мы разбирали node2vec подход. Есть варианты такого вложения при помощи нейронных сетей. Однако, эти подходы опираются на локальную структуру графа, т.е. две вершины получат близкое представление в виде векторов, если они близки в графе. Это хорошо в случае, когда выполняется предположение о наличии свойства групповой эквивалентности (homophily) вершин, но именно структурная эквивалентность двух вершин, далёких в графе в таком представлении не улавливается.

В качестве примера мы можем рассмотреть, например, граф представляющий связи работников некоторого (достаточно большого) завода. Подходы типа node2vec позволяют получить векторное представление вершин при котором, близкими будут вектора, соответствующие работникам одного цеха, а новый подход, должен позволить выявить структурные особенности, т.е. близкими в нём будут вектора начальников цехов, а вектора обычных работников (независимо от цеха) составят в векторном пространстве другой кластер.

Ещё один пример структурно близких вершин из статьи:

здесь вершины $u$ и $v$ структурно похожи, действительно степени у них $5$ и $4$, вершина $u$ присоединина к 3 треугольникам, а вершина $v$ - к двум. К остальной сети эти вершины присоединяются через две вершины. Однако, если $u$ и $v$ в сети находятся на большом расстоянии, то такие подходы как node2vec разместят соответствующие им вектора так же на большом расстоянии.

Перейдём к описанию struc2vec представления вершин.

Мера структурной схожести

Пусть у нас есть неориентированный, невзвешенный граф $\mathcal G = (\mathcal V,\mathcal E)$, $\mathcal V$ - множество вершин, $\mathcal E$ - множество рёбер. Обозначим $R_k(u)$ - множество вершин на расстоянии в точности $k \ge 0$ от вершины $u$. Таким образом $R_1(u)$ - вершины соседние для $u$, а $R_k(u)$ - обзначает кольцо (не круг) вершин на расстоянии $k$.

Введём функцию $s(S)$ - функцию, отображающую подмножество вершин графа $S \subset \mathcal V$ в числовую последовательность степеней вершин из $S$, упорядоченную по возрастанию.

Сравнивая такие упорядоченные последовательности степеней для колец на расстоянии $k$ у пары вершин, можно получить представление о структурной схожести этой пары. Формализуя, авторы вводят понятие структурного расстояния:

\[f_k(u,v) = f_{k-1}(u,v) + g\left(s(R_k(u)),s(R_k(v))\right),\\ k \ge 0,\, \vert R_k(u)\vert > 0,\,\vert R_k(v)\vert > 0\]

здесь $g(D_1, D_2) \ge 0$ расстояние между упорядоченными последовательностями степеней $D_1$ и $D_2$, а $f_{-1} = 0$. Т.к. значения $g(\cdot)$ не отрицательны, то $f_k(u,v)$ не убывает с ростом $k$. Из определения очевидно, что $f_k(u,v)$ определена, только если на расстоянии $k$ и у вершины $u$ и у вершины $v$ есть соседи. Также если $k$-окрестности вершин $u$ и $v$ изоморфны, то $f_{k-1}(u, v) = 0$.

Осталось определить функцию $g(\cdot)$. Эта функция должна измерять расстояние между двумя упорядоченными последовательностями $s(R_k(u)),s(R_k(v)$, эти последовательности могут быть различной длины и состоят из целых чисел (возможно повторяющихся) из отрезка $[0, n-1]$. Авторы предлагают использовать динамическое сопоставление временных последовательностей (Dynamic Time Warping), которое позволяет оптимальным образом сопоставить элементы двух последовательностей $A$ и $B$. Имея функцию расстояния $d(a,b)$, ДСВП алгоритм строит такое сопоставления между элементами последовательностей (не обязательно взаимно-однозначное), чтобы сумма расстояний между сматченными элементами была минимальной.

Для иллюстрации картинка из статьи “FastDTW: Toward Accurate Dynamic Time Warping in Linear Time and Space”:

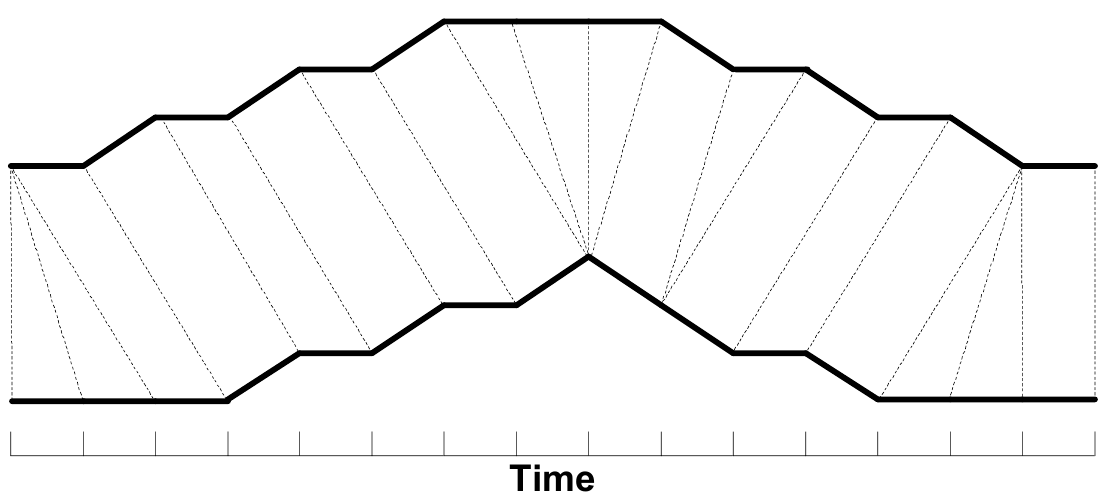
В качестве $d(a,b)$ авторы предлагают использовать:

\[d(a,b) = \frac {\max(a,b)} {\min(a, b)} - 1\]

$a$ и $b$ здесь степени вершин, если они одинаковы $a = b$, то $d(a, b)$ = 0, а значит расстояние между двумя одинаковыми последовательностями степеней будет нулевым. Так же авторы отмечают, что таким образом введенная функция расстояния, сильнее разделяет степени вершины $1, 2$, чем $101, 102$, что соответствует интуиции, вершины у которых $101$ и $102$ соседа, структурно намного более похожи, чем вершина с $1$ соседом и вершина с $2$-мя.

Построение графа контекста

Определившись с метрикой структурной схожести вершин, авторы переходят к построению дополнительного графа контекста.

У нас есть исходный граф $\mathcal G = (\mathcal V,\mathcal E)$, диаметра $d_{\mathcal G}$, будем строить новый взвешенный многоуровневый граф, состоящий из $d_{\mathcal G} + 1$ слоёв, каждый слой $k = 0, …, d_{\mathcal G}$ это полный граф, содержащий все вершины $\mathcal V$ исходного графа и $C_n^2$ рёбер. Вес ребра между вершинами $u$ и $v$ на уровне $k$ определяется формулой:

\[w_k(u, v) = \left\{\begin{matrix} e^{-f_k(u, v)}, &если\, f_k(u, v) \, определена \\ 0, & если\, f_k(u, v) \, не \, определена \end{matrix}\right.\]

Поскольку функция $f_k(u,v)$ определена только, если на расстоянии $k$ и у вершины $u$ и у вершины $v$ есть соседи, для слоёв с $k > d_{\mathcal G}$, очевидно, не будет рёбер с весом больше нуля и значит смысла добавлять слои для таких $k$ - нет. Также надо отметить, что поскольку $f_k(u, v) \ge 0$, то вес ребра находится в интервале $[0, 1]$ и чем больше структурная схожесть двух вершин, тем больше будет вес ребра, которое их соединяет.

Кроме рёбер внутри слоя, добавляются рёбра между слоями, эти рёбра соединяют экземпляры одной и той же вершины на разных слоях вновь построенного графа. Каждая вершина $u_k$, соответствующая на слое $k$ вершине $u \in \mathcal V$ исходного графа связывается с вершинами $u_{k-1}$ и $u_{k+1}$. Рёбрам приписываются веса, согласно формулам:

\[\begin{align*} w(u_k, u_{k+1}) &= \ln(\Gamma_k(u) + e),\, &k = 0, ..., d_{\mathcal G} - 1 \\ w(u_k, u_{k-1}) &= 1,\, &k = 1, ..., d_{\mathcal G} \end{align*}\]

здесь

\[\Gamma_k(u) = \sum_{v \in \mathcal V} \mathbb{1}(w_k(u,v) > \bar{w_k})\]

т.е. количество рёбер инцидентных $u$ вес которых больше, чем средний вес рёбер на уровне $k$. Функция $\Gamma_k(u)$ показывает насколько вершина $u$ похожа на остальные вершины $k$-го слоя. Если на слое $k$ много вершин похожих на $u$, то надо переместится на следующий слой $k+1$, чтобы выделить похожие более точно.

$f_k(u, v)$ неубывает с ростом $k$ и значит вес $w_k(u, v)$ не возрастает. Интуитивно, переход с уровня $k$ на уровень $k+1$ должен снижать количество похожих для данной вершины, но вообще говоря $\Gamma_k(u)$ не обязана убывать, потому что средний вес тоже будет уменьшаться.

Итак в результате получился многослойный граф $\mathcal M$ у которого $n\,d_{\mathcal G}$ вершин и $d_{\mathcal G} C_n^2 + 2n(d_{\mathcal G} - 1)$ рёбер.

Поскольку авторы хотят использовать Skip-Gram подход (который применяется в задачах Natural Language Processing), для “вкладывания” вершин исходного графа в векторное пространство, то следующим шагом надо нагенерировать последовательностей вершин, или, иначе говоря, для каждой вершины сгенерировать контекст.

Генерация контекста для вершин

Для каждой вершины $v \in {\mathcal V}$ исходного графа ${\mathcal G}$ генерируется несколько последовательностей с началом в этой вершине. Для этого используется процесс случайного блуждания (random walk) по графу ${\mathcal M}$, который стартует в вершине, соответствующей $v$ на нулевом уровне.

Процесс устроен следующим образом.

Допустим мы на текущем шаге находимся в вершине $a$ на уровне $k$ графа ${\mathcal M}$, вначале определяем остаться ли на том же уровне (вероятность $q>0$) или (с вероятностью $1-q$) перейти на уровень $k-1$ или $k+1$. Если принято решение остаться на том же уровне, то вероятность $p_k(a,b)$ перейти в вершину $b$ определяется весом рёбер инцендентных текущей вершине:

\[p_k(a,b)=\frac {e^{-f_k(a,b)}} {Z_k(a)},\; Z_k(a) = \sum_{t\in V, t \neq a} e^{-f_k(a,t)}\]

Поскольку структурно похожие вершины у нас связывают рёбра большего веса, то соответственно и в последовательность вероятнее будет набрать вершины структурно схожие. Т.е. контекст исходной вершины будет формироваться из вершин структурно схожих с ней.

Если же решено перейти на другой уровень, то вероятность перейти на $k-1$ или $k+1$ уровень так же пропорциональна весу соответствующих ребер:

\[\begin{align*} p_k(a_k,a_{k+1}) &= \frac {w_k(a_k, a_{k+1})} {w_k(a_k, a_{k+1}) + w_k(a_k, a_{k-1})},\\ p_k(a_k,a_{k-1}) &= \frac {w_k(a_k, a_{k-1})} {w_k(a_k, a_{k+1}) + w_k(a_k, a_{k-1})} \end{align*}\]

Осталось на полученных последовательностях вершин натренировать Skip-Gram и таким образом получить представление вершин в векторном пространстве.

Оптимизации

Для достаточно большого исходного графа, построение многослойного графа ${\mathcal M}$ задача накладная и по вычислительным ресурсам и по памяти. Авторы предлагают несколько вариантов оптимизации.

1. Уменьшение длины последовательности степеней вершин (OPT1)
2. Уменьшение количества рёбер для которых вычисляются веса (OPT2). Очевидно, что если у одной вершины степень $3$, а у другой $300$, то уже на нулевом уровне структурное расстояние между ними будет достаточно большим (а соответственно вес ребра малым) и нет смысла считать веса на следующих уровнях
3. Уменьшение числа слоёв (OPT3). С ростом $k$ разница $\vert f_k(u,v) -f_{k+1}(u,v) \vert$ становится всё меньше и меньше и структурную схожесть вершин зачастую можно определить ограничившись количеством слоёв в графе ${\mathcal M}$ меньшим, чем $d_{\mathcal G}$

Эксперименты

В качестве первого эксперимента авторы рассматривают $(h,k)$ - граф-штангу ($(h,k)$ - barbell graph).

$(h,k)$ - граф-штанга это граф, который состоит из трёх частей: двух полных графов $K_1$ и $K_2$ (каждый из $h$ вершин) и пути $P$ длины $k$, который соединяет $K_1$ и $K_2$. Две вершины $b_1\in K_1$ и $b_2\in K_2$ выступают в качестве зацепления, к ним присоединяются соответственно вершины $p_1$ и $p_k$ пути $P = {p_1, p_2, …, p_k}$.

Очевидно, у такого рода графов, много структурно идентичных вершин. Например, все вершины из объединения множеств $C_1=K_1\setminus{b_1}$ и $C_2=K_2\setminus{b_2}$ структурно эквивалентны, можно даже построить изоморфизм на любой паре таких вершин. Также структурно эквивалентны любые пары вершин $(p_i, p_{k-i})$ для $i=1,…,(k-1)$, и наконец пара вершин $(b_1, b_2)$.

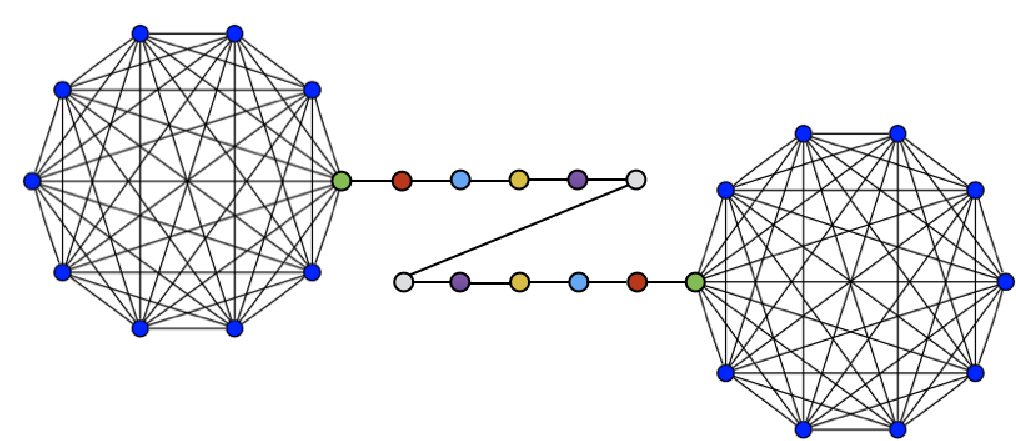
Авторы берут $(10, 10)$ граф-штангу и применяют различные алгоритмы для получения представления вершин в виде элементов векторного пространства $\mathbb{R}^2$ (проще говоря точек на плоскости).

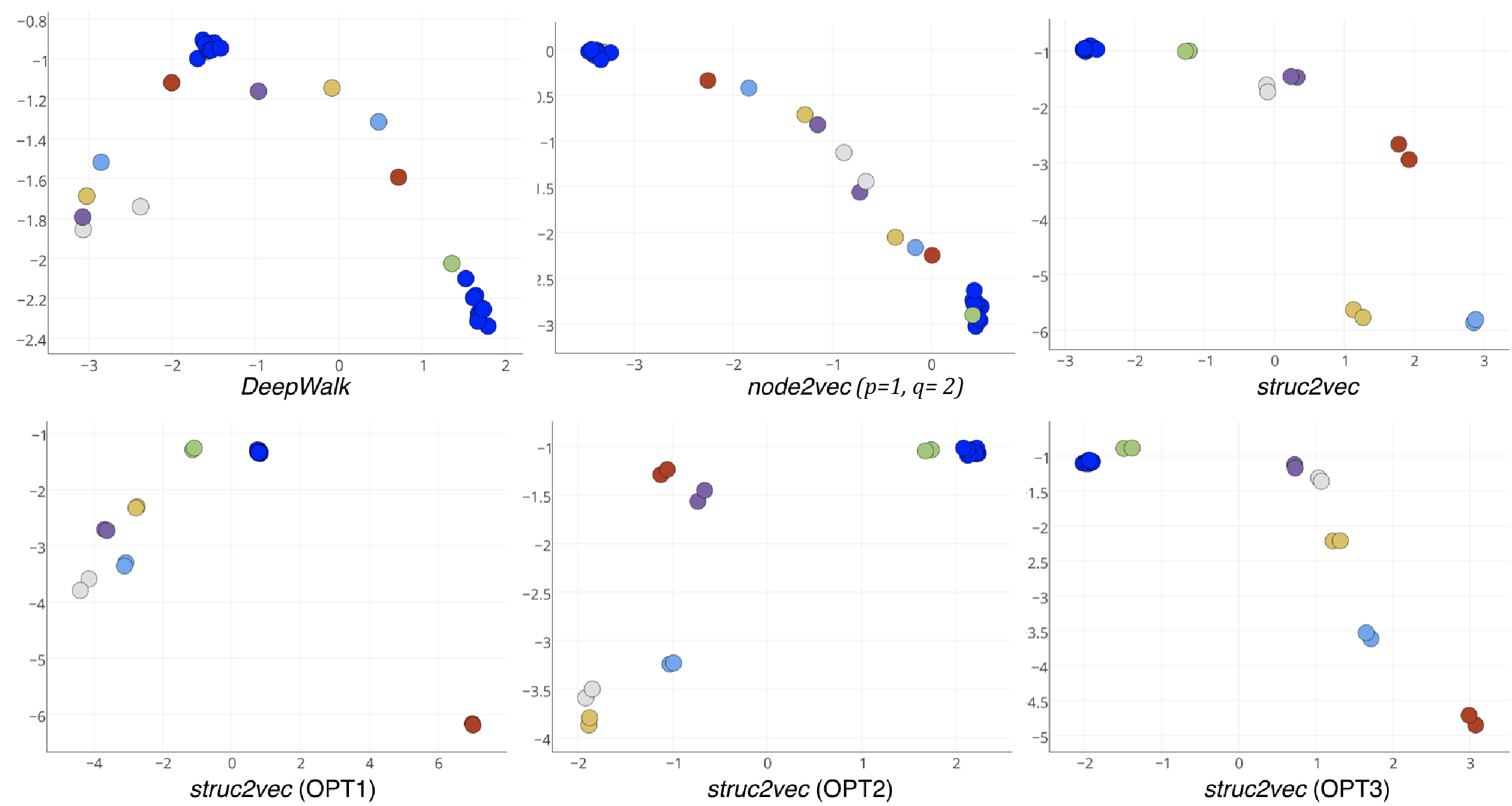
Очевидно, что struc2vec во всех вариантах, наиболее точно позволяет ухватить структурную идентичность вершин и построить соответсвующее отображение.

Для второго эксперимента авторы берут Zachary’s Karate Club, причем они его берут в двух экземплярах и складывают в один граф, добавив ребро между 1-й и 37-й (которая есть дубль 1-й) вершинами, чтобы граф стал связным.

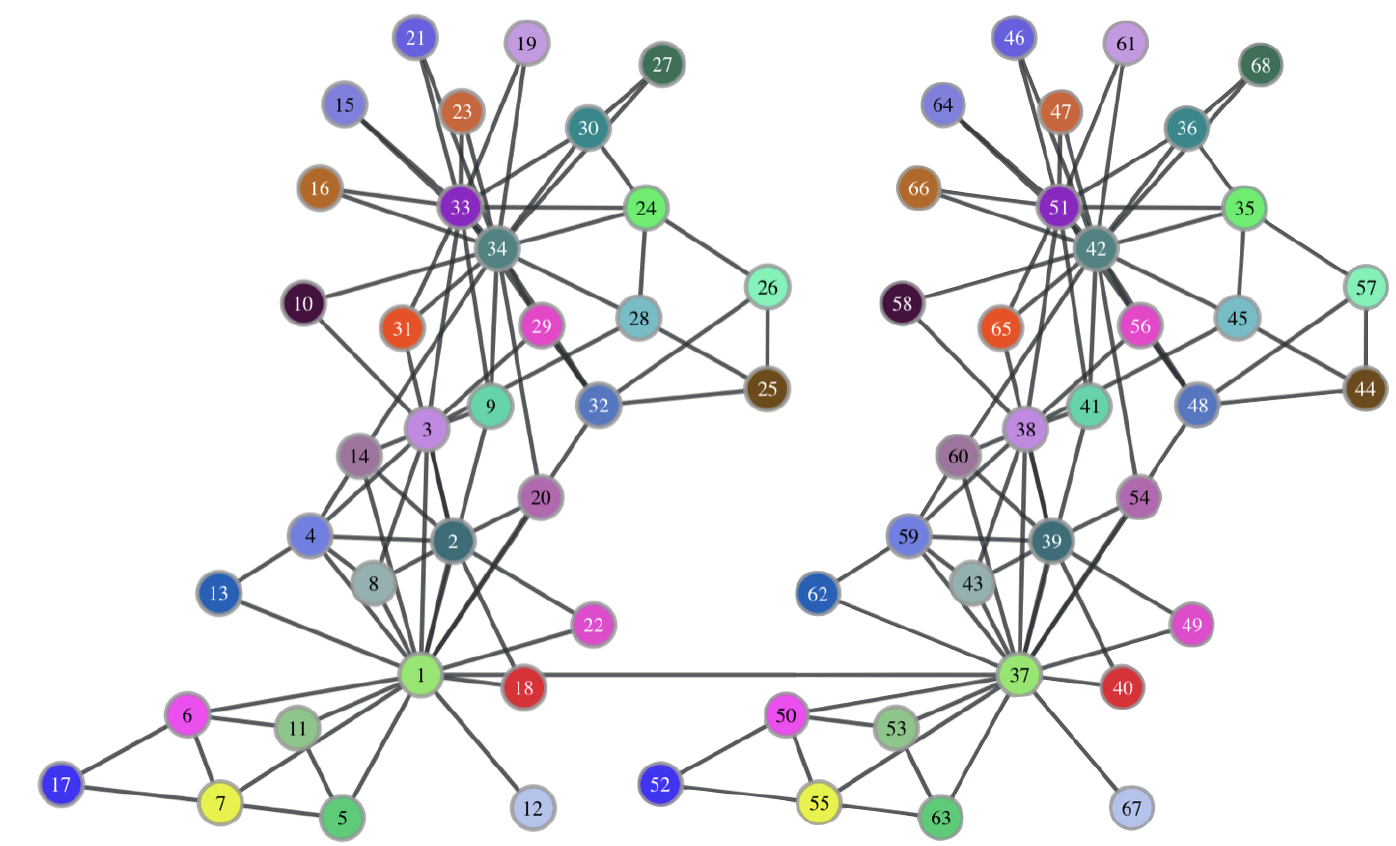
Авторы опять применяют node2vec, DeepWalk и свой алгоритм:

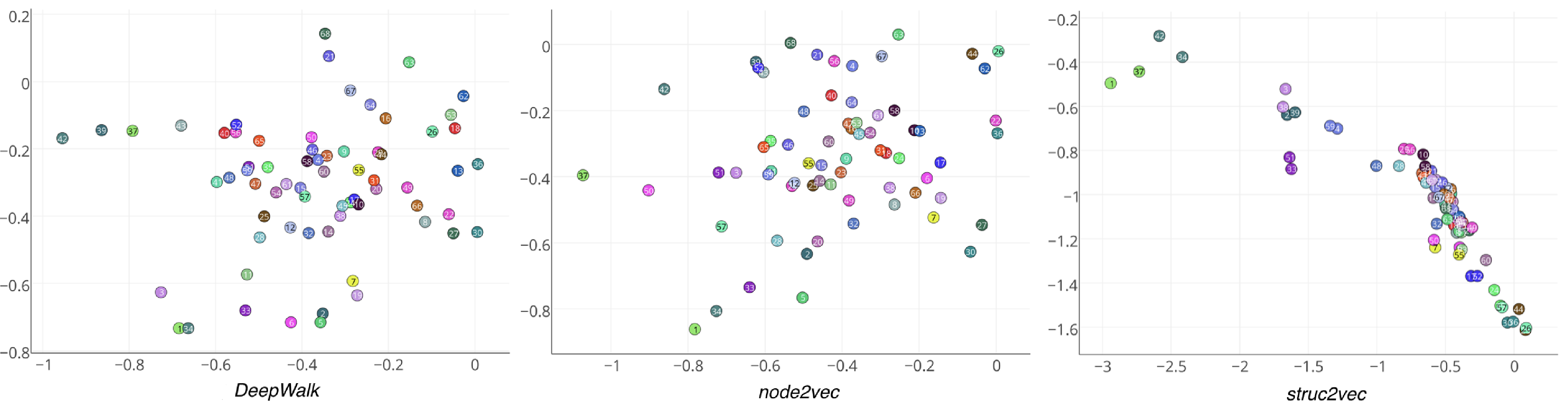
Очевидно, что и node2vec, DeepWalk не смогли разместить парные вершины близко в векторном пространстве, а struc2vec не только выявил парные вершины, но и выделил в отдельный кластер две пары вершины 1, 37 и 34, 42 - которые соответствуют инструктору и администратору клуба. Так же есть еще несколько кластеров, которые выделил struc2vec алгоритм и которые действительно соответствуют “структурно идентичным” членам клуба.

Выводы

Подход интересный, и наверное, в каких-то ситуациях работает лучше других, но не очень понятно насколько большие графы можно “прожевать” при таких не маленьких потребностях в вычислительных мощностях и памяти.