Глубокое взаимное обучение

Дата: 28 декабря 2021.

Разобрал уже два варианта knowledge distillation в первом случае данные передавались от очень большой сети (учителя) к маленькой (ученику) напрямую, а во втором обучение происходило через посредника - сетку среднего размера (помошника учителя). Авторы статьи, рассматриваемой сегодня, предлагают подход, который они назвали глубокое взаимное обучение (deep mutual learning (DML)): несколько небольших сеток обучаются одновременно обмениваясь между собой знаниями во время обучения.

Возникает вопрос почему такое взаимное обучение должно привести к хорошим результатам (лучшим, чем просто обучение отдельной нейронной сети)? Авторы обосновывают это тем, что все малые сетки с каждым шагом тренировки должны всё лучше и лучше интерполировать вероятности принадлежности подаваемого на вход объекта одному из классов, но при этом вероятности остальных классов у каждой из сетей будут распределены по разному (поскольку обучение стартует с разных начальных весов, даже если структура сетей одинакова), и обмениваясь вот этой информацией сети и дообучают друг друга.

Разберёмся со случаем взаимного обучения двух сетей, расширить его на случай, когда сетей больше можно будет очевидным образом. Итак у нас есть две сети для классификации, на конце каждой есть softmax слой:

\[P^{(k)}_i = \frac {\exp (z^{(k)}_i)} {\sum_j \exp (z^{(k)}_j)},\, i=1,...,M,\, k=1, 2\]

который преобразует logits $z^{(k)}$ в вероятности. В качестве штрафной функции при тренировке классификатора используется кроссэнтропия. Если взять набор пар объект-класс: $<X_i, Y_i>, \, i = 1, …, N$, то можно это расписать как:

\[\mathcal L^{(k)}_{CE} = - \sum_{s=1}^{N} \sum_{i=1}^M [i = Y_s] \ln (P^{(k)}_i(X_s))\]

Авторы предлагают добавить в функцию штрафа, в качестве дополнительного слагаемого, расстояние Кульбака — Лейблера между распределениями, получаемыми на выходе сетей (надо отметить что расстояние КЛ не симметрично):

\[D_{KL}(P^{(2)} || P^{(1)}) = \sum_{s=1}^{N} \sum_{i=1}^M P^{(2)}_i(X_s) \ln \frac {P^{(2)}_i(X_s)} {P^{(1)}_i(X_s)},\\ D_{KL}(P^{(1)} || P^{(2)}) = \sum_{s=1}^{N} \sum_{i=1}^M P^{(1)}_i(X_s) \ln \frac {P^{(1)}_i(X_s)} {P^{(2)}_i(X_s)}\]

Таким образом для первой сети получаем функцию штрафа:

\[\mathcal L^{(1)} = \mathcal L^{(1)}_{CE} + D_{KL}(P^{(2)} || P^{(1)})\]

а для второй:

\[\mathcal L^{(2)} = \mathcal L^{(2)}_{CE} + D_{KL}(P^{(1)} || P^{(2)})\]

Во время тренировки, авторы предлагают брать минибатч высчитывать на нём вероятности с помощью первой и второй сетей, затем обновить веса первой сети, снова пересчитать вероятностные распределения (только первой сети) и обновить веса второй сети.

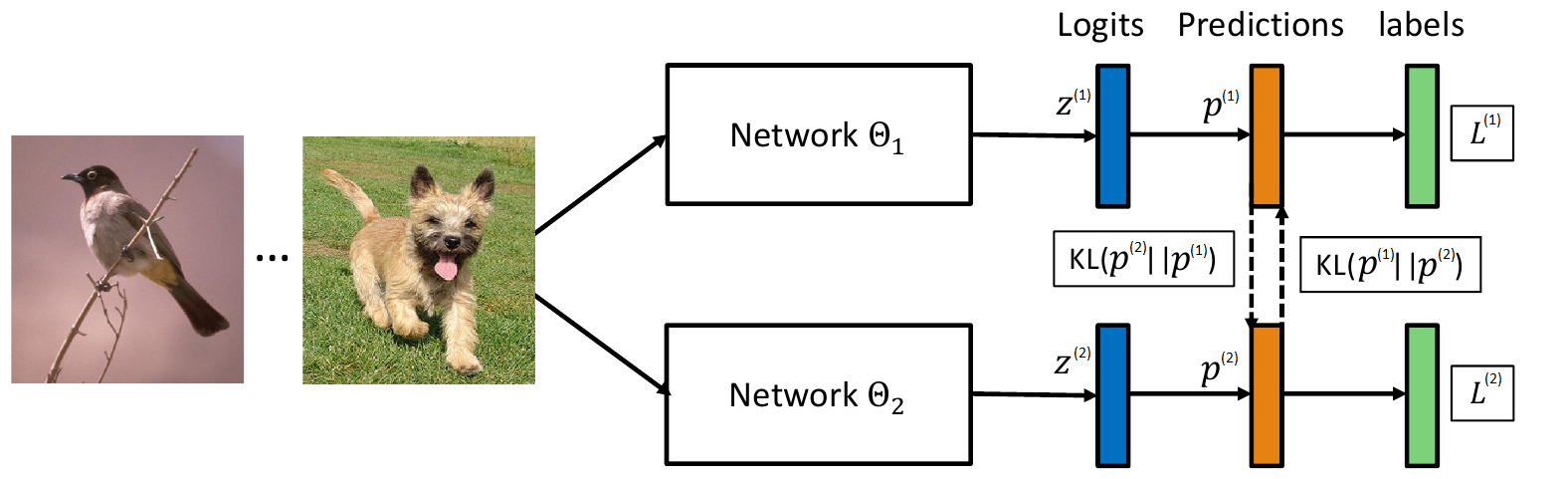
Схема взаимного обучения, изображение из статьи

В случае если одновременно хотим обучить $T > 2$ нейронных сетей, то возможно два варианта обобщения:

Добавим в функцию штрафа среднее арифметическое расстояний КЛ до вероятностных распределений всех сетей кроме данной:
\[\mathcal L^{(t)} = \mathcal L^{(t)}_{CE} + \frac 1 {T-1} \sum_{k=1, k\neq t}^{T} D_{KL}(P^{(k)} || P^{(t)})\]
В функции штрафа заменим второе слагаемое на расстояние КЛ до усредненного распределения всех сетей кроме данной:
\[\mathcal L^{(t)} = \mathcal L^{(t)}_{CE} + D_{KL}(P^{(avg)} || P^{(t)}),\, P^{(avg)} = \frac 1 {T-1} \sum_{k=1, k\neq t}^{T} P^{(k)}\]

Второй вариант на тестах показывает себя хуже и это логично объясняется тем, что у среднего распределения пик вероятности для “правильного” класса выражен значительно ярче, а весь смысл knowledge distillation в использовании сглаженных распределений для улучшения обучения.

Эксперименты

Для экспериментов авторы используют датасеты CIFAR-100 и Market-1501 и сети ResNet-32, MobilNet, InceptionV1 и Wide ResNet WRN-28-10.

Сети существенно варьируются по количеству параметров:

--------------------------------------------------------------------------------
                             | ResNet-32 | MobileNet | InceptionV1 | WRN-28-10 |
--------------------------------------------------------------------------------
кол-во параметров (миллионы) |       0.5 |       3.3 |         7.8 |      36.5 |
--------------------------------------------------------------------------------

На CIFAR-100 авторы тренировали сети ResNet-32, MobileNet и WRN-28-10 как независимо, так и в парах:

-------------------------------------------------------------------------------
        Модели        |    Независимо   | Взаимное обучение |    Улучшение    |
 Модель 1 |  Модель 2 |   М1   |   М2   |    М1   |    М2   |   М1   |   М2   | 
-------------------------------------------------------------------------------
ResNet-32 | ResNet-32 | 68.99% | 68.99% |  71.19% |  70.75% |  1.20% |  1.76% |
WRN-28-10 | ResNet-32 | 78.69% | 68.99% |  78.96% |  70.73% |  0.27% |  1.74% |
MobileNet | ResNet-32 | 73.65% | 68.99% |  76.13% |  71.10% |  2.48% |  2.11% |
MobileNet | MobileNet | 73.65% | 73.65% |  76.21% |  76.10% |  2.56% |  2.45% |
WRN-28-10 | MobileNet | 78.69% | 73.65% |  80.28% |  77.39% |  1.59% |  3.74% |
WRN-28-10 | WRN-28-10 | 78.69% | 78.69% |  80.28% |  80.08% |  1.59% |  1.39% |
-------------------------------------------------------------------------------

Столбец “Улучшение” показывает прирост качества сети полученной при взаимном обучении относительно той же модели обученной независимо.

Из таблицы видно, что при взаимном обучении качество растет а) для всех моделей б) при любом сочетании пар моделей. Т.е. даже “маленький” ResNet позволяет улучшить качество “огромной” WRN-28-10 хотя и незначительно.

На Market-1501 авторы тренировали MobileNet (отдельно и в паре) и тоже получили значительное улучшение при взаимном обучении.

Следующая серия экспериментов сравнивает взаимное обучение и обучение малой сети при помощи большой:

------------------------------------------------------------------------------------
 Датасет    |          Модели         |    Независимо   | 1 -> 2 |  Взаимное обуч. |
            |  Модель 1   |  Модель 2 |   М1   |   М2   |        |   М1   |    М2  |
------------------------------------------------------------------------------------
CIIFAR-100  | WRN-28-10   | ResNet-32 | 78.69% | 68.99% | 69.48% | 78.96% | 70.73% |
            | MobileNet   | ResNet-32 | 73.65% | 68.99% | 69.12% | 76.13% | 71.10% |
------------------------------------------------------------------------------------
Market 1501 | InceptionV1 | MobileNet | 65.26% | 46.07% | 49.11% | 65.34% | 52.87% |
            | MobileNet   | MobileNet | 46.07% | 46.07% | 45.16% | 52.95% | 51.26% |
------------------------------------------------------------------------------------

в столбце “1 -> 2” результат тренировки с использованием knowledge distillation, где натренированная сеть с моделью 1 передаёт знание сети с моделью 2. И снова взаимное обучение показывает результаты лучше.

Далее авторы изучают вопрос сказывается ли количество одновременно взаимно обучаемых сетей на конечное качество. Для этого они запускают тренировку нескольких MobileNet на датасете Market-1501 меряют средний mAP и стандартное отклонение:

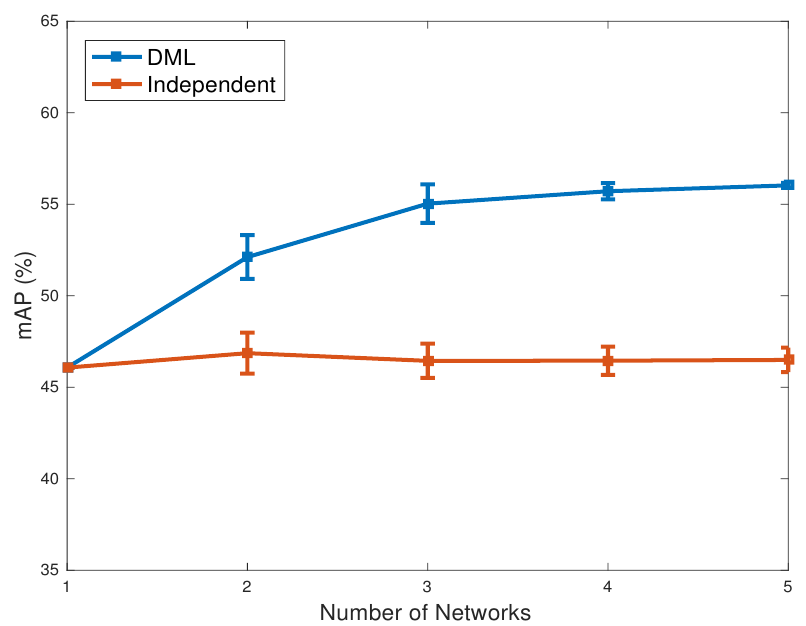
График зависимости качества от кол-ва учеников, изображение из статьи

Из графика видно, что с увеличением числа учеников качество сетей обученных совместно растет, при этом снижается стандартное отклонение, т.е. еще и обобщающая способность повышается.

Далее авторы пробуют обученные только что сетки использовать не по отдельности, а в виде ансамбля:

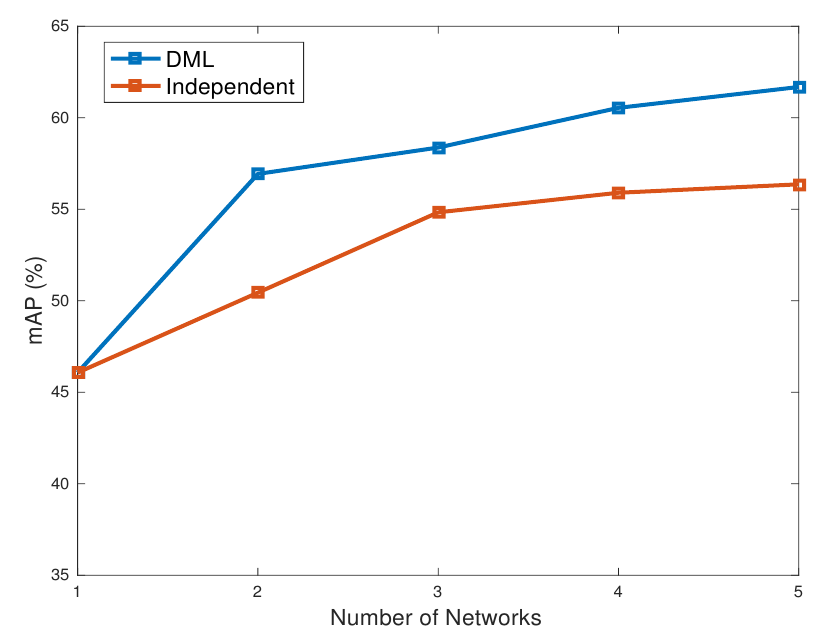
График зависимости качества ансамбля от кол-ва учеников, изображение из статьи

Из графика видно, что ансамбль индивидуально обученных сетей наращивает качество, относительно отдельной сети (это вполне очевидно), но вариант ансамбля из взаимно обученных сетей и здесь показывает результаты лучше.