arXiv:1912.02292

В прошлый раз смотрели статью, которая разбирала проблему компромисса смещения-дисперсии (bias-variance trade-off) и вводила понятие двойного спуска. В этой статье на конкретных примерах было показано, что вместо выбора модели сбалансированной между недообученностью и переобученностью сложности, как это обычно предлагается в классическом машинном обучении, можно “переусложнить” модель добившись нулевой или близкой к нулю ошибки на тренировочных данных и при этом получить на тестовых данных результаты лучше чем в сбалансированном варианте.

Новая статья продолжает копать в том же направлении. Авторы показывают, что не только усложнение (увеличение числа параметров) модели приводит ко второму спаду, но и увеличение числа эпох тренировки. В статье вводится понятие эффективной сложности модели, которое объединяет в себе и сложность модели и длительность тренировки.

Так же авторы показывают, что эффект пика и двойного спуска, крайне ярко проявляется при зашумленности тестовых данных, а переусложнение модели позволяет с зашумленностью бороться.

В качестве затравки график качества на тренировочных и тестовых данных из CIFAR-10:

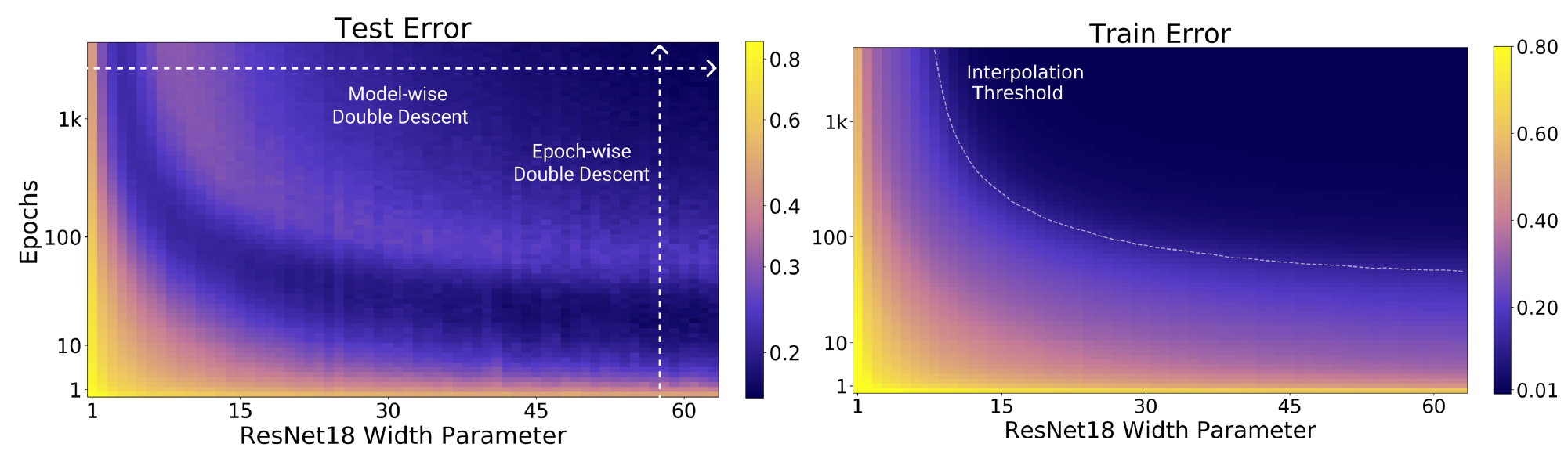
В качестве модели использовалась ResNet18 с разным числом фильтров в свёрточных слоях $[k, 2k, 4k, 8k]$ (для модели из исходной статьи про ResNet: $k=64$). На графиках видно, что эффект двойного спада наблюдается как при увеличении сложности модели, так и при увеличении длительности тренировки.

Эффективная сложность модели

Для некоторой формализации, авторы статьи вводят понятие эффективная сложность модели (Effective Model Complexity). Пусть у нас есть некоторый набор размеченных данных $S =\{(x_1, y_1), …,(x_n, y_n)\}$, $x_k\in\mathbb{R}^d$, $y_k \in \mathbb{R}$, соответствующий, распределению ${\mathcal D}$. Процедура тренировки ${\mathcal T}$, используя этот набор, строит классификатор ${\mathcal T}(S)$. Эффективной сложностью модели ${\mathcal T}$ авторы предлагают называть максимальное число примеров $n$ на которых средняя ошибка ${\mathcal T}$ близка к нулю. Более формально:

Определение. Эффективной сложностью модели тренировочной процедуры ${\mathcal T}$ по отношению к распределению ${\mathcal D}$ и точности $\varepsilon > 0$ назовем:

\[EMC_{\mathcal{D}, \varepsilon}({\mathcal T}) = \max\left\{n\vert \mathbb{E}_{S\sim{\mathcal D}} \left[Error_{S}({\mathcal T}(S))\right]\le \varepsilon \right\}\]

здесь $Error_{S}(M)$ - средняя ошибка модели $M$ на тренировочном наборе $S$.

Рассмотрим задачу предсказания на основе $n$ примеров из распределения $\mathcal{D}$, которую будем решать тренируя в качестве классификатора процедурой $\mathcal{T}$ нейронную сеть. Авторы выдвигают гипотезу, что для достаточно малого $\varepsilon>0$, можно рассмотреть три ситуации:

1. Недопараметризованный режим. Если $EMC_{\mathcal{D}, \varepsilon}({\mathcal T})$ достаточно меньше, чем $n$, то любое изменение $\mathcal{T}$, которое увеличит эффективную сложность модели, в свою очередь приведёт к уменьшению ошибки на тестовых данных.

2. Перепараметризованный режим. Если $EMC_{\mathcal{D}, \varepsilon}({\mathcal T})$ достаточно больше, чем $n$, то любое изменение $\mathcal{T}$, которое увеличит эффективную сложность модели, в свою очередь приведёт к уменьшению ошибки на тестовых данных.

3. Критический режим. Если $EMC_{\mathcal{D}, \varepsilon}({\mathcal T}) \approx n$, то любое изменение $\mathcal{T}$, которое увеличит эффективную сложность модели, может привести как к уменьшению так и к увеличению ошибки на тестовых данных.

Авторы сами отмечают, что гипотеза эта очень неформальная. Потому что не вполне ясно какое брать $\varepsilon$, а термины достаточно меньше и достаточно больше вызывают определенные вопросы. Однако, эксперименты, которые авторы провели, показывают наличие критического интервала вокруг порога интерполяции, когда $EMC_{\mathcal{D}, \varepsilon}({\mathcal T}) = n$, вне этого интервала, увеличение сложности приводит к росту точности, а вот внутри - может как улучшить, так и ухудшить ситуацию. Ширина интервала зависит от данных и от процедуры тренировки, но как именно у авторов статьи ответа нет.

Переходим к собственно экспериментам, которые представлены в статье.

Двойной спад при увеличении сложности модели

В некотором смысле это повторение экспериментов исходной статьи про двойной спад, однако, на других моделях нейронных сетей и других датасетах, дополнительно в тренировочную часть датасета может быть внесен шум. Внесение шума вероятности $p$ в разметку (label noise) означает, что каждому элементу данных из датасета с вероятностью $(1-p)$ присвоена правильная метка, и с вероятностью $p$ метка, выбранная равномерно и случайно из всех возможных в данном датасете. Такой шум вносится до начала тренировки и в течении тренировки метки не меняются.

Сложность модели

Итак первый набор графиков показывает зависимость ошибки тренировки и тестов на датасете CIFAR-10:

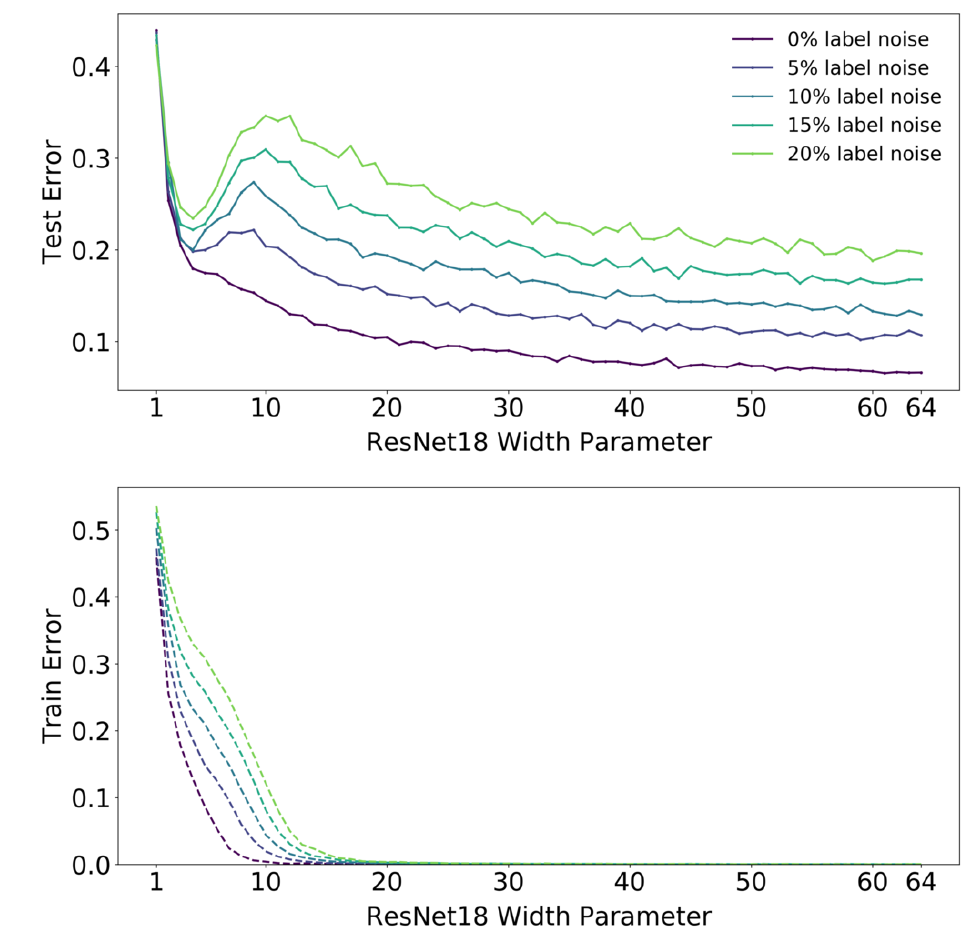
в качестве классификатора используется сеть ResNet18 с разным числом фильтров в свёрточных слоях (см. выше). Видно, что для случая, когда в тренировочные данные не вносился шум, то при сложности модели в районе порога интерполяции на тестовых данных наблюдается “плато”, которое при увеличении сложности переходит в спад. Для случая когда тренировка происходит на зашумленных данных, при примерно тех же параметрах сложности модели наблюдается увеличение ошибки на тестовых данных, которое тем больше, чем больше искажений внесено в тренировочный датасет, и снова увеличение сложности приводит к уменьшению ошибки.

Аналогичные графики для ResNet18, но на CIFAR-100:

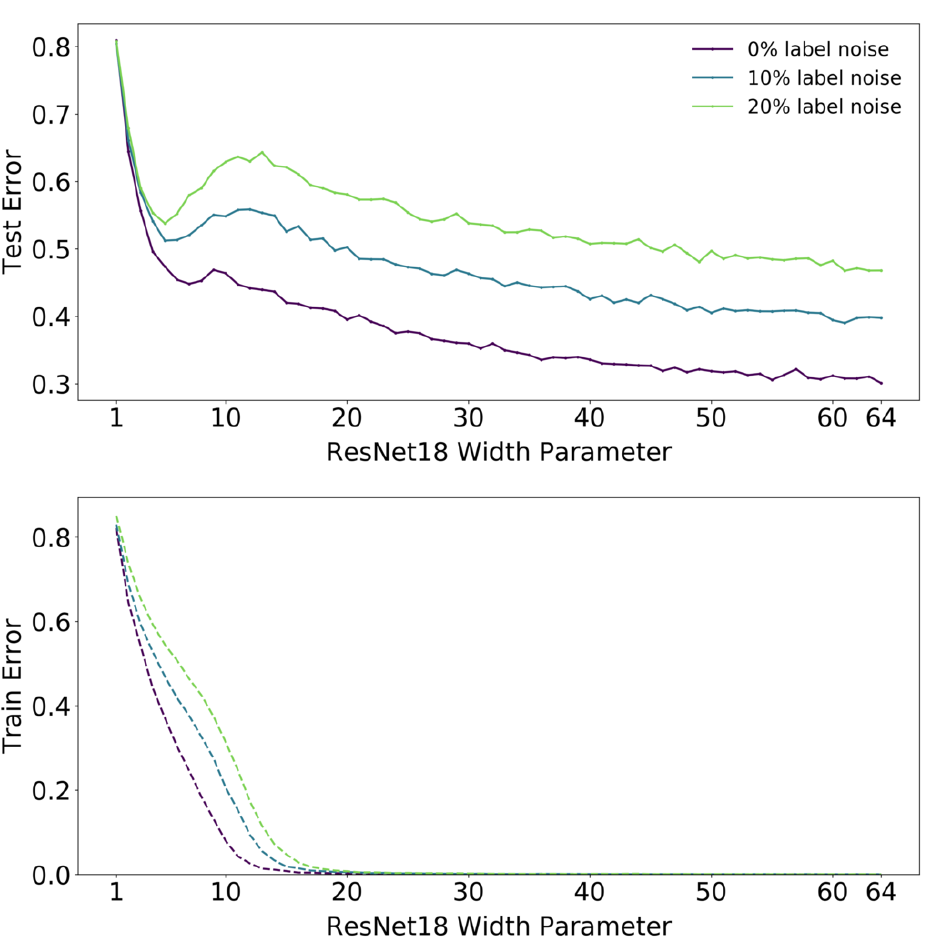
В отличии от CIFAR-10 здесь даже для незашумленного тренировочного набора, получаем пик на тестовых данных в районе порога интерполяции.

Можно сделать вывод, что увеличение сложности модели позволяет побороть зашумленность тренировочных данных.

Замечание. В обоих случаях тренировали с использованием Adam оптимизатора 4К эпох.

Data Augmentation

Следующий эксперимент использует обычную свёрточную сеть из 5 слоёв с количеством фильтров $[k, 2k, 4k, 8k]$ и полносвязным слоем для классификации на конце. Используется датасет CIFAR-10, проверяется влияние расширения данных (data augmentation) на порог интерполяции:

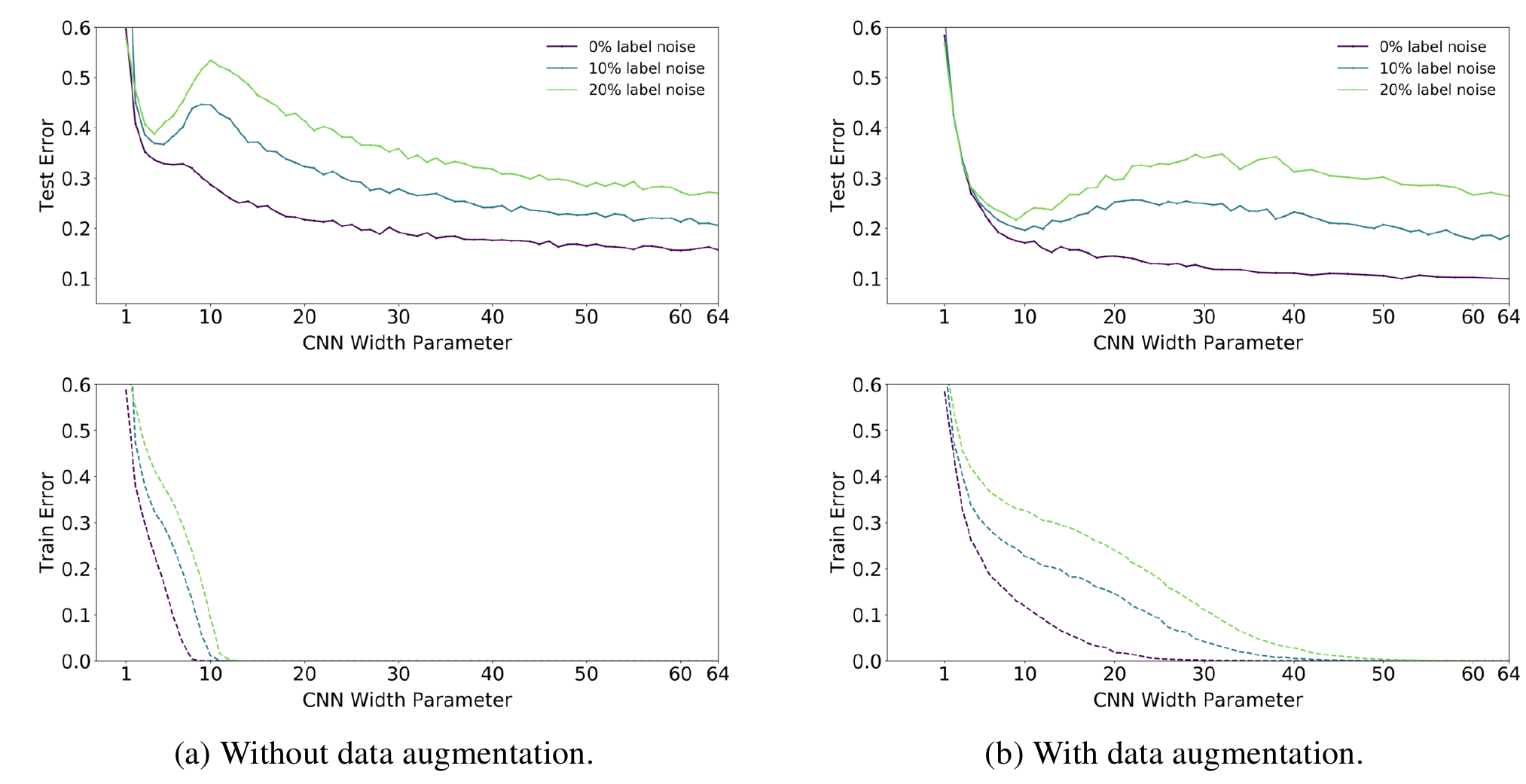
Из графиков можно сделать вывод, что процесс расширения данных сдвигает вправо (в сторону увеличения сложности) порог интерполяции, синхронно сдвигая и пик ошибки на тестовых данных (в то же время сглаживая величину пика).

Замечание. В обоих случаях тренировали с использованием SGD оптимизатора 500К шагов.

Оптимизаторы SGD vs Adam

Еще один эксперимент сравнивающий разные оптимизаторы. Сверточная сеть из предыдушего пункта тренируется на датасете без зашумления и расширения данных с использованием SGD оптимизатора 500К шагов и с использованием Adam 4K эпох:

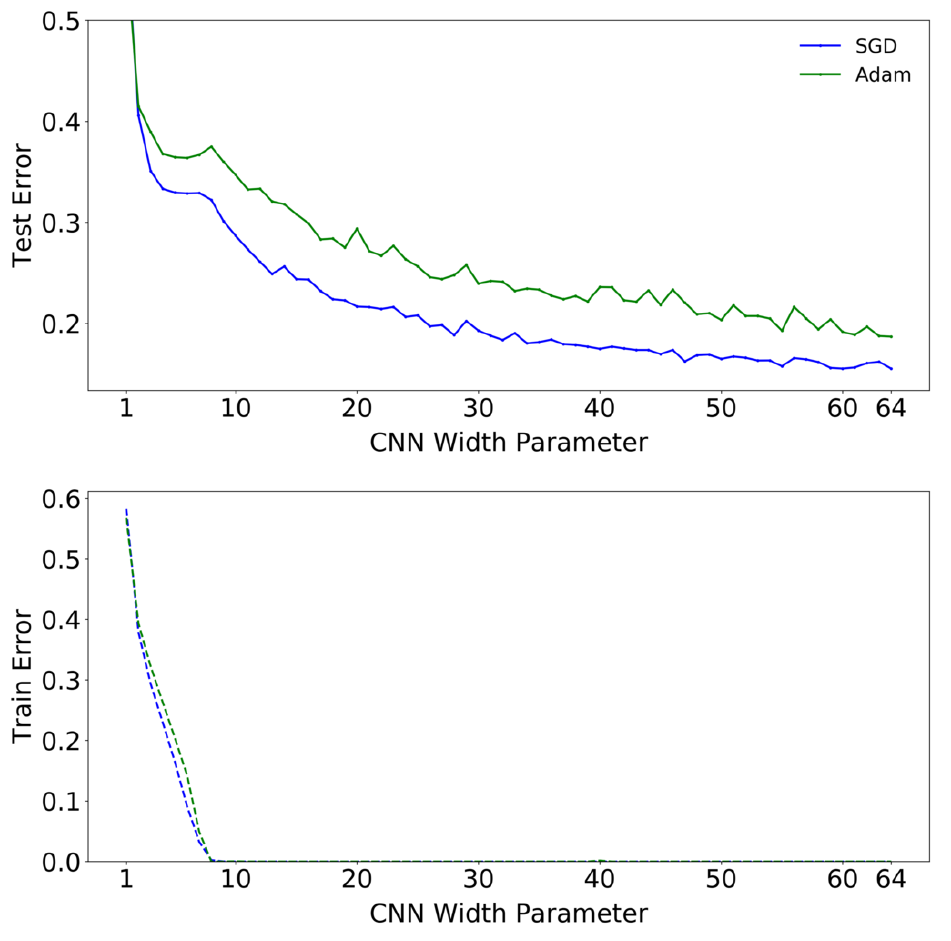
Сложность модели и длительность тренировки

Теперь авторы проводят эксперимент для выяснения связи сложности модели и длительности тренировки. CIFAR-100, свёрточная сеть из 5 слоёв, данные без зашумления и расширения и SGD в качестве оптимизатора:

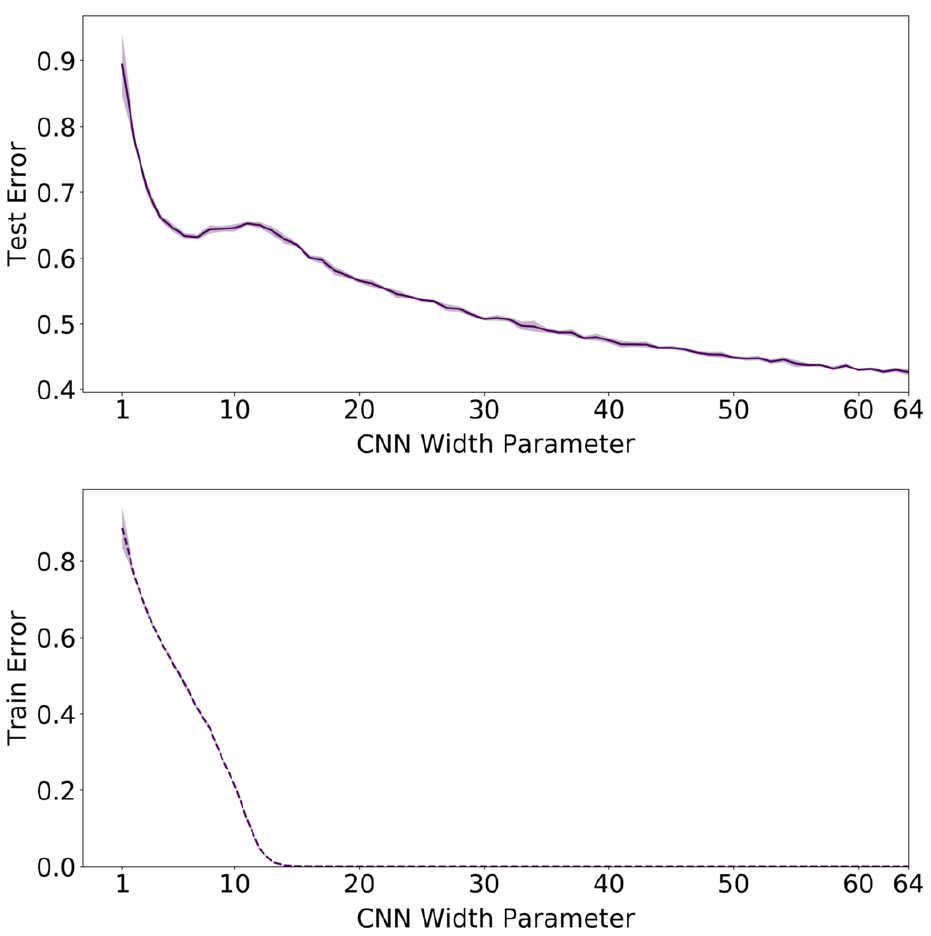
Видно пик на тестовых данных.

Для этого же эксперимента зависимость точности и от сложности модели и от длительности тренировки:

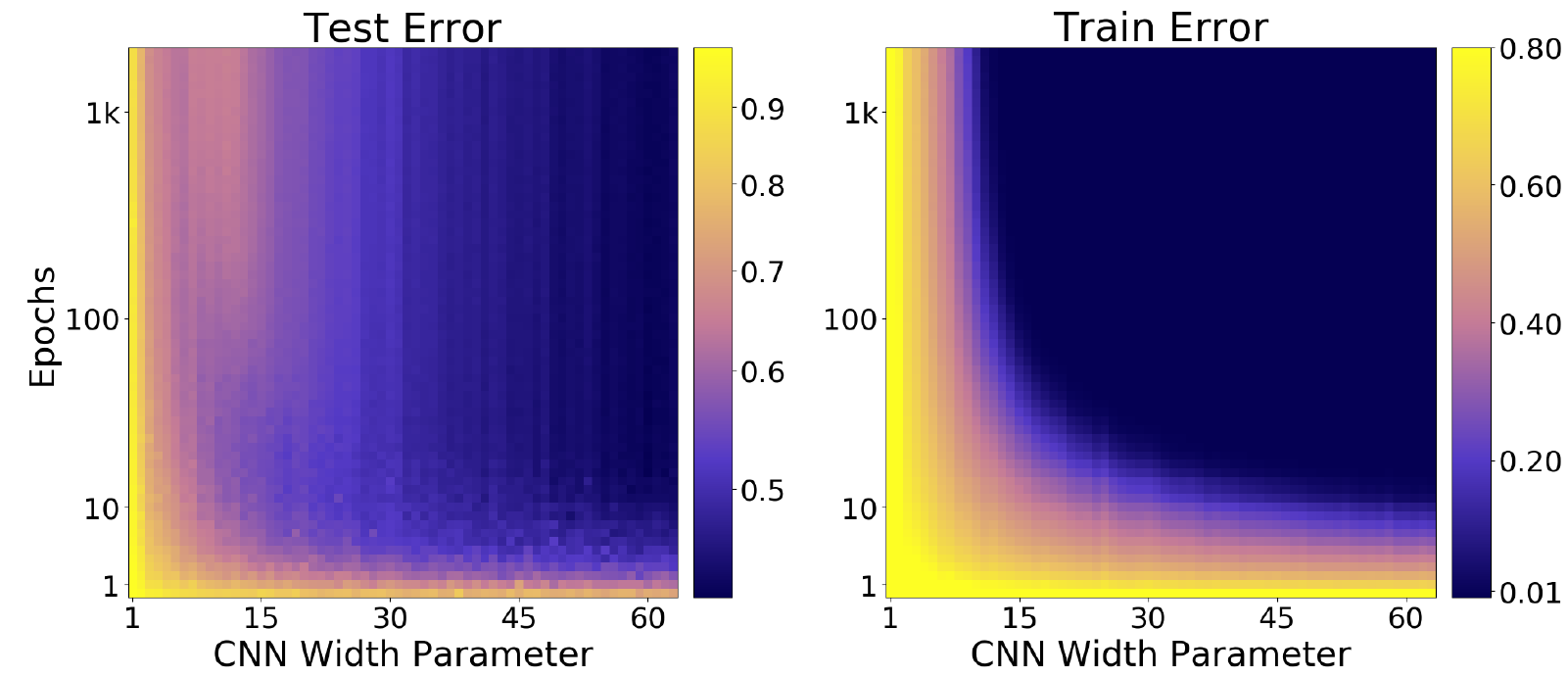
И наконец, динамика ошибки на тестовых данных:

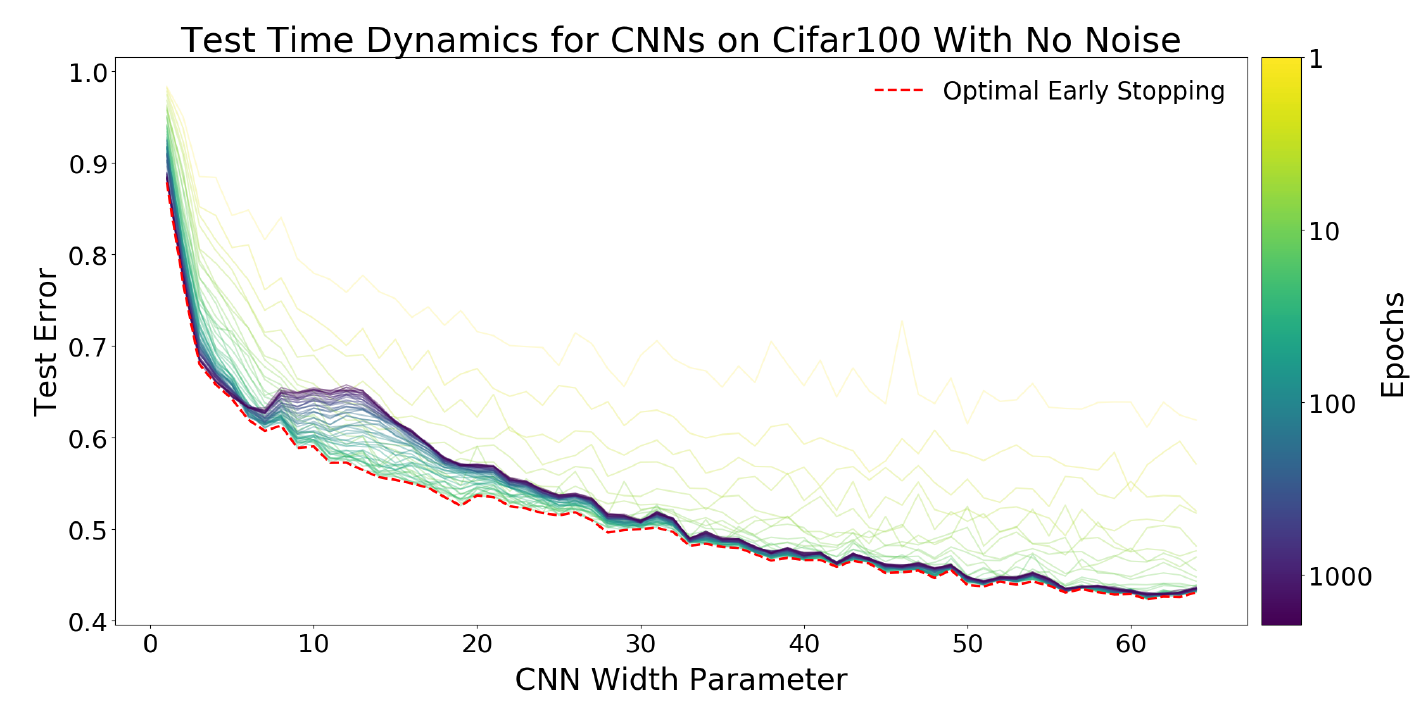
Из экспериментов ясно, почему для “слабых” моделей нужно использовать “раннюю остановку” тренировки.

Длительность тренировки

В следующей части работы, авторы изучают эффект двойного спада в зависимости от количества эпох, которые тренировалась модель.

Снова тренируется набор ResNet сетей разного размера на датасете CIFAR-10 с внесенным 20% шумом, в качестве оптимизатора используется Adam, график показывает зависимость качества, полученной сети на тестовых данных от размера и длительности тренировки:

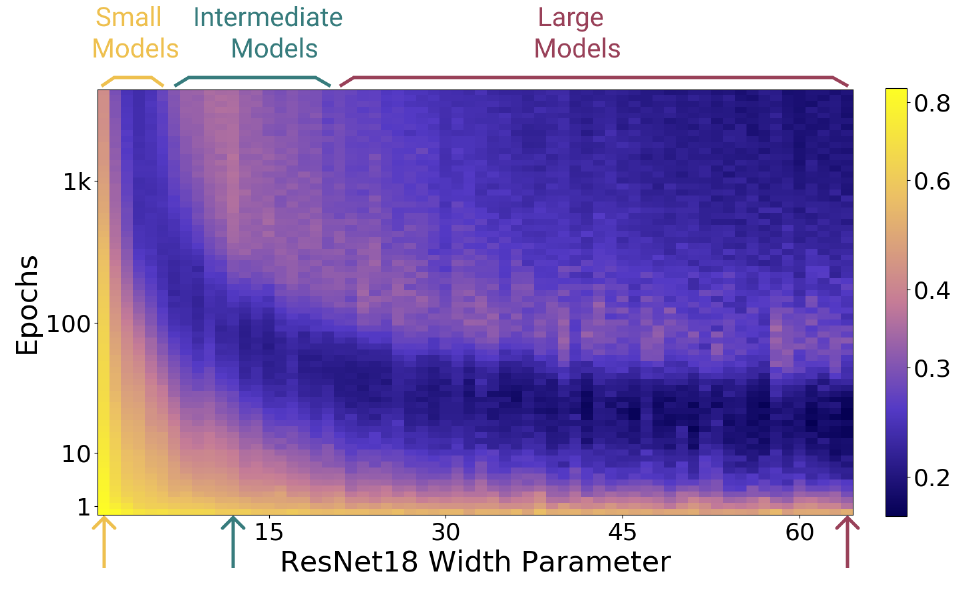
авторы разбивают модели по сложности на три класса: маленькие, среднии и большие. График зависимости качества на тестовых данных от длительности тренировки (взято по одному представителю из каждого класса моделей):

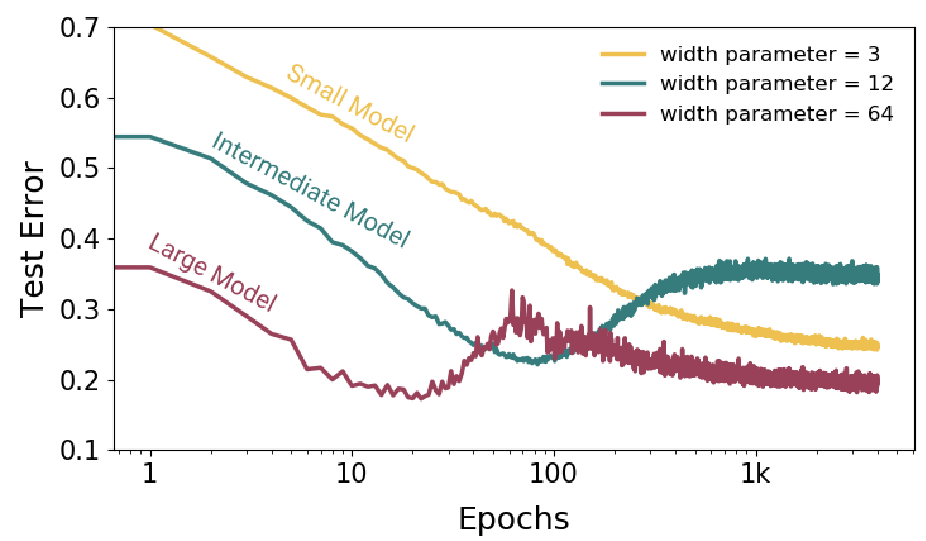
Сложность маленьких моделей такова, что они всегда находятся в зоне недообученности, т.е. не могут на тренировочных данных получить ошибку “близкую к нулю”. Для таких моделей увеличение длительности тренировки, может привести только к улучшению качества работы на тестовых данных (правда в конечном итоге все упирается в некоторый порог ниже которого не опускается).

Для средних моделей имеем класическую U-кривую, когда начиная с некоторого порога интерполяции, качество на тренировочных данных ухудшается, а второго спада достичь продолжением тренировки не удаётся (на самом деле среднии модели и на тренировочных данных не получают обычно нулевую ошибку). Для таких моделей следует использовать “раннюю остановку”, чтобы получить хорошие результаты.

Наконец, для больших моделей мы наблюдаем “двойной спуск”, на каком-то этапе качество на тестовых данных падает, но если продолжить тренировку, то оно вновь начинает расти и в конечном итоге получается лучше чем в момент приближения к порогу интерполяции слева.

Далее авторы проводят эксперименты с разными моделями сетей и разными датасетами (в разной степени зашумленными), показывая, что и здесь присутствует эффект двойного спада при увеличении длительности тренировки.

ResNet18 и CIFAR-10:

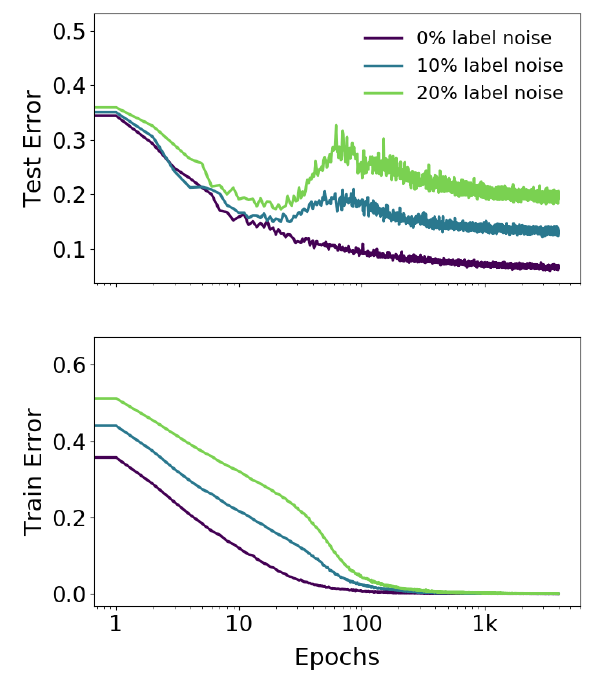
ResNet18 и CIFAR-100:

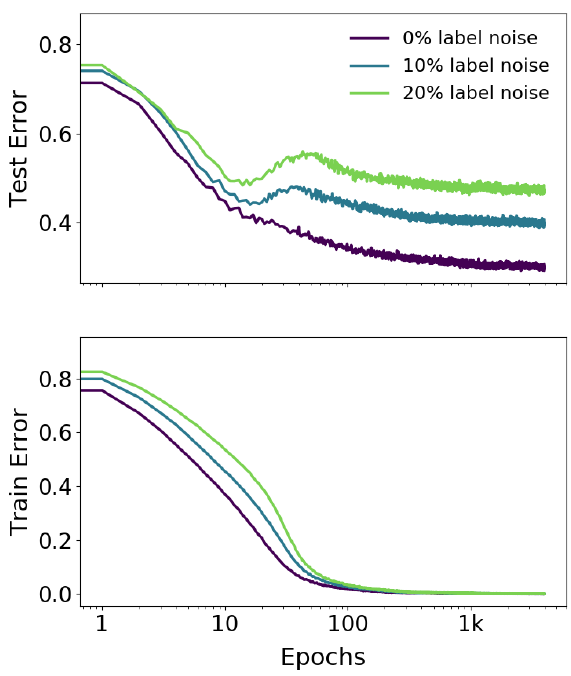
5-слойная CNN и CIFAR-10:

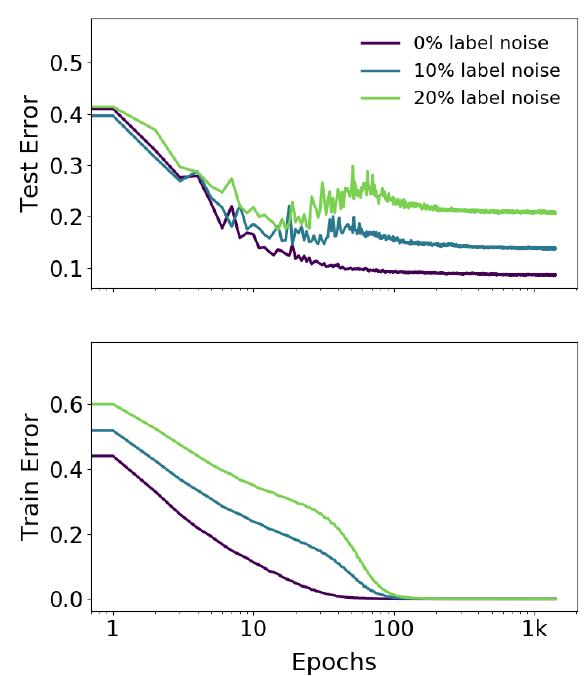
Замечание. Надо отметить, что в данном случае эффект двойного спада проявляется на зашумленных данных, в случае, когда тренировочные данные не испорчены пика (или даже плато) практически не видно.

Размер тренировочного датасета

Еще один набор экспериментов, в которых меняется объем данных, используемых для тренировки. Тренируется снова 5-слойные CNN (разного размера) на CIFAR-10:

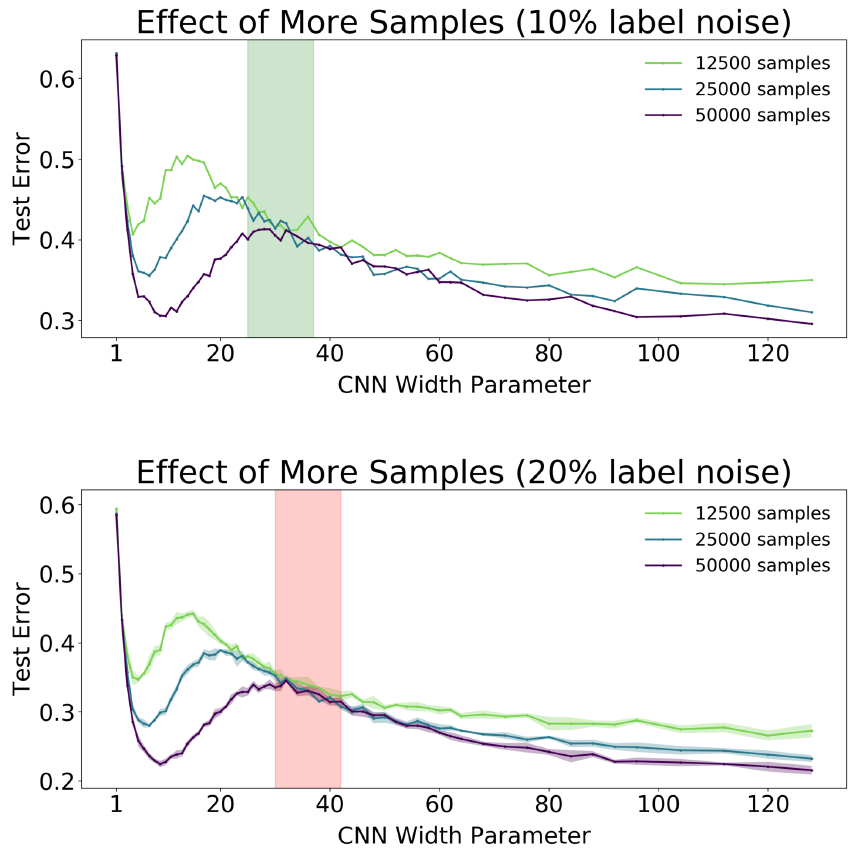
На верхнем графике зашумленность тренировочных данных 10%, на нижнем зашумленность - 20%.

Наблюдается хорошо известный тезис: “чем больше данных тем лучше”, т.е. одна и таже модель, показывает лучшее качество при увеличении объёма тренировочных данных, однако, так же видно что в некоторой области параметра сложности модели, рост объема тренировочных данных не приводит к улучшению качества. Для верхнего графика - зеленая полоса, где рост тренировочных данных вдвое не даёт уменьшения ошибки. Для нижнего графика - розовая полоса - область, где даже рост объёма тренировочных данных вчетверо, также не приводит к улучшению качества.

Также на обоих графиках очевидно наблюдается сдвиг “пика” ошибок вправо с ростом объема тренировочных данных.

Наконец, еще два графика, зависимость ошибок на тренировочной и тестовой части для маленькой, средней и большой модели:

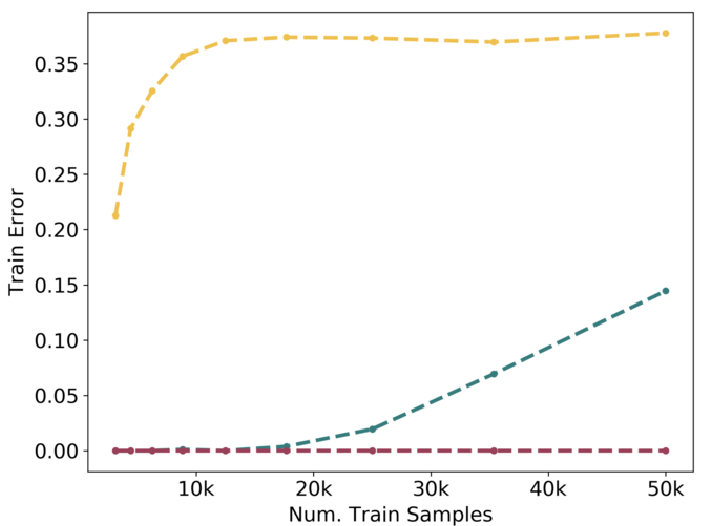
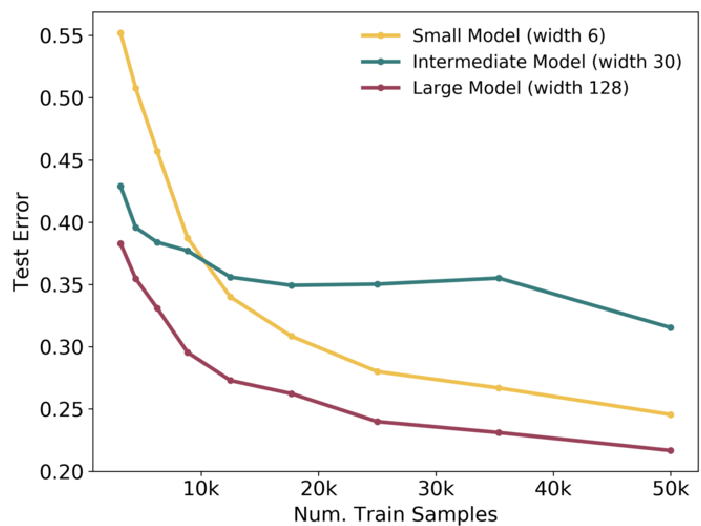
Это снова 5-слойные CNN на CIFAR-10 с зашумлением 20%. Заметно, что увеличение размера датасета хорошо помогает маленьким и большим моделям, а вот средним - не слишком.