arXiv:2008.05258

После появления нейронных сетей особенно глубоких, основная проблема “где найти размеченный датасет для решаемой задачи?”. Особенно остро такая проблема стоит во всевозможных задачах компьютерного зрения. И если для детектирования и классификации изображений разметка датасета штука крайне недешевая, то для семантической сегментации, удаления шума и прочих удалений отражений разметка датасета может стоить просто дико дорого.

Поэтому приходится каким-то образом ловчить и приспосабливаться. Можно, например, генерировать синтетический датасет (это хорошо получается, если учесть развитие всевозможных игровых движкоd), и тренировать сетку на нем, одновременно, решая задачу domain adaptation, согласуя синтетические данные с реальными.

Другой подход - это так называемое полуконтролируемое обучение (semi-supervised learning). В этом случае разметку имеет не весь датасет, а только его часть, но неразмеченные данные также используются в процессе обучения. Этот метод широко используется в задачах классификации. Однако, для пиксельных задач: семантической сегментации, удаления шума, улучшение ночных фотографий и т.п., подходы применяемые в классификации не применимы.

Сегодня разберем статью, в которой автор предлагают SSL методику для решения пиксельных задач.

Введение

Итак авторы рассматривают несколько “пиксельных задач”: семантическая сегментация, отделение основного объекта на изображении от фона, удаление шума с изображения, улучшение ночных снимков (часть из них задачи пиксельной классификации, например, семантичекая сегментация, часть - регрессии). Для решения всех задач в рамках SSL авторы предлагают единую схему:

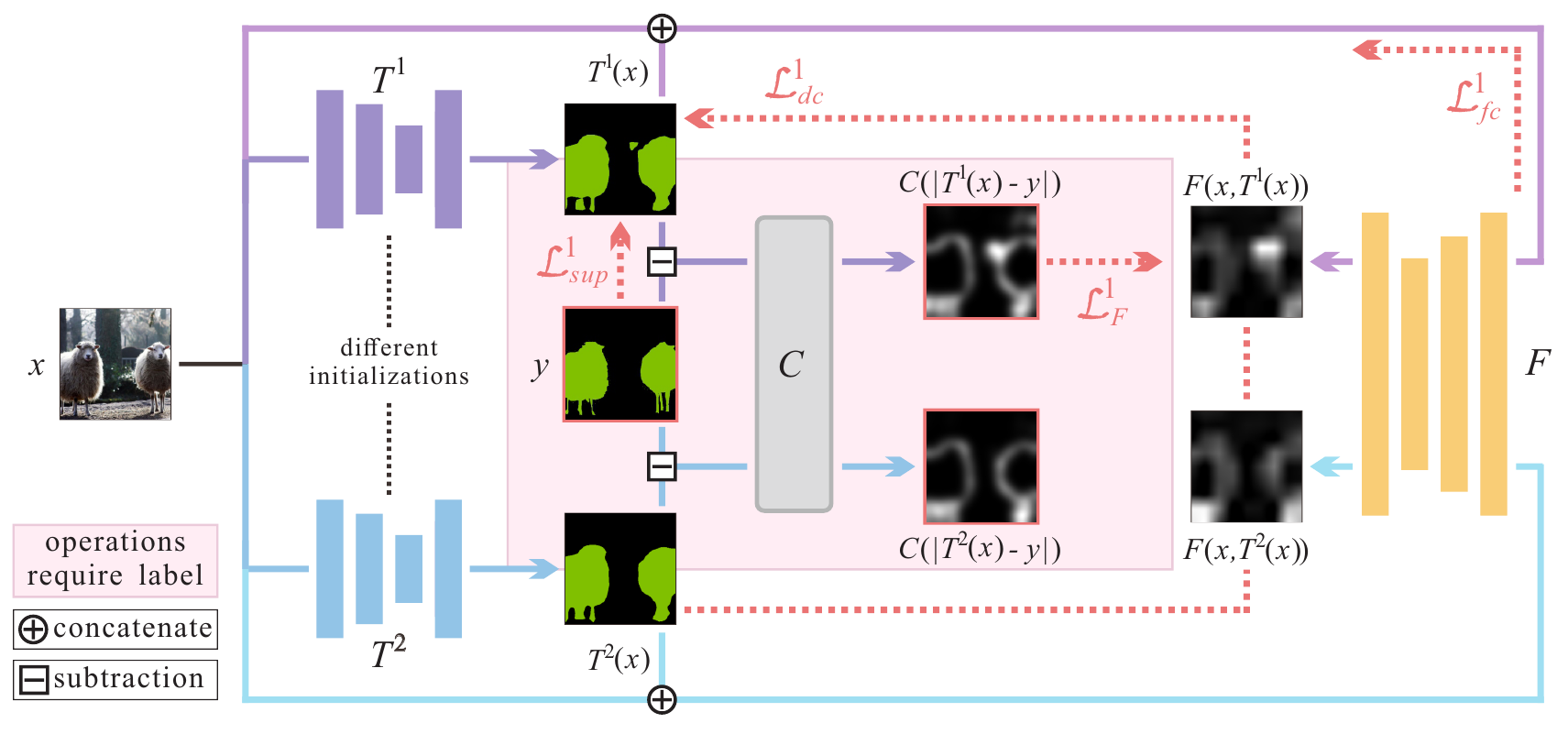
Разберемся подробнее. Итак у нас есть датасет ${\mathcal X} = {\mathcal X}_l \cup {\mathcal X}_u$, который состоит из двух частей: ${\mathcal X}_l$ - размеченной и ${\mathcal X}_u$ - неразмеченной. Возьмем две нейронных сети, которые решают нашу задачу: $T^{(1)}, T^{(2)}$, сетки могут иметь разную структуру (кол-во слоёв, кол-во каналов в слоях и т.п., для сегментации, например, можно в качестве $T^{(1)}$ взять DeepLab, а в качестве $T^{(2)}$ - UNet), а могут быть и одной и той же моделью, однако, в последнем случае крайне важно, чтобы начальная инициализация весов у этих двух сетей отличалась. Собственно, на этом различии строится вся дальнейшая схема (чем то это похоже на глубокое взаимное обучение, которое мы в своё время разбирали).

Итак у нас есть две сети, каждая из которых решает исходную задачу, т.е. преобразует изображение $T^{(k)}: {\mathbb R}^{H \times W \times 3} \rightarrow {\mathbb R}^{H \times W \times O}$. Здесь $O$ - размерность результата и зависит от задачи, для семантической сегментации $O$ - есть кол-во классов, а для задачи удаления шума на выходе получаем снова изображение и $O=3$.

В дополнении к этим двум сеткам авторы заводят третью сеть $F$ - дефектометр, которая для каждого пикселя определяет вероятность того, что отклик от сети $T^{(k)}$ в этом пикселе неправильный:

\[F: {\mathbb R}^{H \times W \times (O + 3)} \rightarrow [0, 1]^{H \times W \times 1}\]

На вход дефектометра подаётся объединение (по последней размерности) исходного изображения и отклика от сети: $F(x, T^{(k)}(x))$, а сама функция $F$ - это просто свёрточная нейронная сеть из нескольких слоёв, часть из которых со страйдом большим 1, а заключительный слой - апскейл до размеров исходного изображения.

Далее схема тренировки похожа на тренировку GAN. На каждой итерации, мы делаем два шага тренировки:

1. Тренируем модели $T^{(k)}, k=1,2$ при фиксированном дефектометре $F$. На данном шаге мы используем и размеченную и неразмеченную части датасета.

2. Тренируем дефектометр $F$ при фиксированных $T^{(k)}, k=1,2$, используя только размеченную часть датасета.

Замечание: поскольку вначале тренировки дефектометр у нас выдаёт случайный отклик, то влияние штрафных функций основанных на отклике дефектометра вначале убирается коэффициентами в ноль и затем возрастает на более поздних итерациях.

Тренировка моделей

Для тренировки моделей $T^{(k)}, k=1,2$ используется следующая штрафная функция:

\[{\mathcal L}^{(k)}_T({\mathcal X}, {\mathcal Y}) = \sum_{<x_l, y>}{\mathcal L}^{(k)}_{sup}(x_l, y) + \sum_x\left(\lambda_{dc}\, {\mathcal L}^{(k)}_{dc}(x) + \lambda_{fc}\, {\mathcal L}^{(k)}_{fc}(x)\right)\]

Первое слагаемое:

\[{\mathcal L}^{(k)}_{sup}(x_l, y) = \sum_{h,w,o}{\mathcal R}(T^{(k)}(x_l)^{(h,w,o)}, y^{(h,w,o)})\]

считается на размеченной части датасета ($x_l, y$ - пара картинка-разметка). ${\mathcal R}(\cdot, \cdot)$ - штрафная метрика, которая зависит от того какую задачу решаем (например, для семантической сегментации это может быть кроссэнтропия, а для удаления шума MSE).

Второе слагаемое - динамическая согласованность моделей (Dynamic Consistency Constraint) опирается на отклик дефектометра:

\[{\mathcal L}^{(k)}_{dc}(x) = \frac 1 2 \sum_{h, w}\left(m_{dc}^{(k)}(x)^{(h,w)}\sum_{o}\left(T^{(k)}(x)^{(h, w, o)} - T^{(\tilde{k})}(x)^{(h, w, o)}\right)^2\right)\]

здесь $\tilde{k}$ это дополнительная для $k$-ой модели, т.е. $\tilde{k} = 1$, если $k = 2$ и $\tilde{k} = 2$, если $k = 1$. $k$-ая модель штрафуется здесь в тех пикселях, где дефектометр считает, что она ошиблась сильнее своей товарки:

\[m_{dc}^{(k)}(x)^{(h,w)} = \left\{\begin{matrix} 1, & \hat F\left(x, T^{(k)}(x)\right)^{(h, w)} > \hat F\left(x, T^{(\tilde{k})}(x)\right)^{(h, w)}\\ 0, & \hat F\left(x, T^{(k)}(x)\right)^{(h, w)} \leq \hat F\left(x, T^{(\tilde{k})}(x)\right)^{(h, w)} \end{matrix}\right.\]

здесь вместо непосредственно дефектометра $F$ используется:

\[\hat F(x, T^{(k)})^{(h,w)} = \left\{\begin{matrix} F(x, T^{(k)})^{(h,w)}, & F(x, T^{(k)})^{(h,w)} < \xi \\ 1, & F(x, T^{(k)})^{(h,w)} \geq \xi \end{matrix}\right.\]

чтобы не штрафовать модели в тех пикселях, где они обе сильно ошиблись ($\xi$ - порог, который выбирается в зависимости от задачи).

Наконец, последнее слагаемое штрафует там, где обе модели выдали плохой, с точки зрения дефектометра отклик:

\[{\mathcal L}_{fc}^{(k)}(x) = \frac 1 2 \sum_{h, w}\left(m_{fc}(x)^{(h,w)}\left(F(x, T^{(k)}(x))^{(h, w)} - 0\right)^2\right)\] \[m_{fc}(x)^{(h,w)} = \left\{\begin{matrix} 1, & F\left(x, T^{(1)}(x)\right)^{(h, w)} > \xi\, {\rm AND}\, F\left(x, T^{(2)}(x)\right)^{(h, w)} > \xi\\ 0, & F\left(x, T^{(1)}(x)\right)^{(h, w)} \leq \xi\, {\rm OR}\, F\left(x, T^{(2)}(x)\right)^{(h, w)} \leq \xi \end{matrix}\right.\]

стараясь сделать так, чтобы модель удовлетворила дефектометр.

Тренировка дефектометра

Дефектометр тренируется на размеченной части датасета. Мы фиксируем обе модели $T^{(k)}, k=1,2$ и используем штрафную функцию:

\[{\mathcal L}^{(k)}_F({\mathcal X}_l, {\mathcal Y}) = \sum_{<x_l, y>}\left(\frac 1 2 \sum_{h,w}\left(F(x_l,T^k(x_l))^{(h, w)} - C(|T^k(x_l) - y|)^{(h,w)}\right)^2 \right)\]

В качестве ground truth можно было бы использовать просто ошибку модели, т.е. $|T^k(x_l) - y|$ (возможно усредненную по каналам и нормализованную, поскольку дефектометр должен выдавать вероятность, т.е. значения из отрезка $[0, 1]$ для каждого пикселя изображения), но авторы считают, что лучше подвергнуть этот тензор дополнительным преобразованиям, которые сгладят исходную разность.

$C(\cdot)$ - берет усредненный по каналам модуль разности $|T^k(x_l) - y|$ и применяет последовательно несколько фильтров блюра и дилейта, в заключении нормализуя результат преобразований.

Для понимания картинка из статьи:

Результаты

Авторы проверили свой фреймворк на нескольких задачах. Мне наиболее интересна задача семантической сегментации. Для нее авторы взяли датасет Pascal VOC 2012 добавили Segmentation Boundaries Dataset и использовали модель DeepLab-v2. Одновременно, они тренировали пару таких моделей с дефектометром в рамках своего подхода и отдельно модель саму по себе. Пробовали они это делать, оставив размеченной $1 / 16$, $1 / 8$, $1 / 4$, $1 / 2$ части датасета. Во всех случаях использование описанного в статье подхода дало прирост качества порядка $3$%, кроме случая, когда оставили разметку на половине датасета, в этом случае прирост был около $1.5$%, т.е. качество в любом случае возрастает.

Забавно, что в случае, когда оставили только четверть разметки, использования SSL подхода выдаёт качество выше, чем тренировка без SSL на датасете с половиной разметки.

Вывод

Крайне познавательная статья, надо будет попробовать на своих задачах.