arXiv:2004.01673

И еще про особые точки. Однако, здесь концепция несколько отличается от двух предыдущих статей (SuperPoint, D2-Net). Если раньше мы брали две картинки, на каждой находили особые точки с дескриптором в каком-то векторном пространстве, а потом тем или иным способом “матчили” особые точки опираясь на их близость в пространстве дескрипторов и это называлось sparse-to-sparse методика. То в данной статье предлагается использовать несимметричный sparse-to-dense подход, а именно, вначале найти особые точки на одном изображении, а потом для каждой найденной точки искать соответствие на втором.

Итак, допустим у нас есть два изображения $I_1$ и $I_2$ и мы хотим найти множество пар связанных между собой точек на этих изображениях: $\left \{ \left(p^k_1, p^k_2\right) \right \}_{k=1}^N$.

Для этого нам надо научиться интерполировать условную вероятность вида $P(p_2 \vert I_1, I_2, p^k_1)$ и тогда не сложно будет определить точку соответствующую $p^k_1$ как $p^k_2 = \arg\max_{p_2 \in I_2} P(p_2 \vert I_1, I_2, p^k_1)$. Авторы предлагают параметризировать условную вероятность в виде:

\[P(p_2 | I_1, I_2, p^k_1, \Theta) = \frac {\exp \left( C_k(p_2) \right)} {\sum_{q \in I_2} \exp \left( C_k(q) \right)}\]

а $C_k(\cdot) = C(I_1, I_2, p^k_1, \Theta)(\cdot)$ функция, которая будет представлена в виде свёрточной нейронной сети. Выглядеть это должно следующим образом:

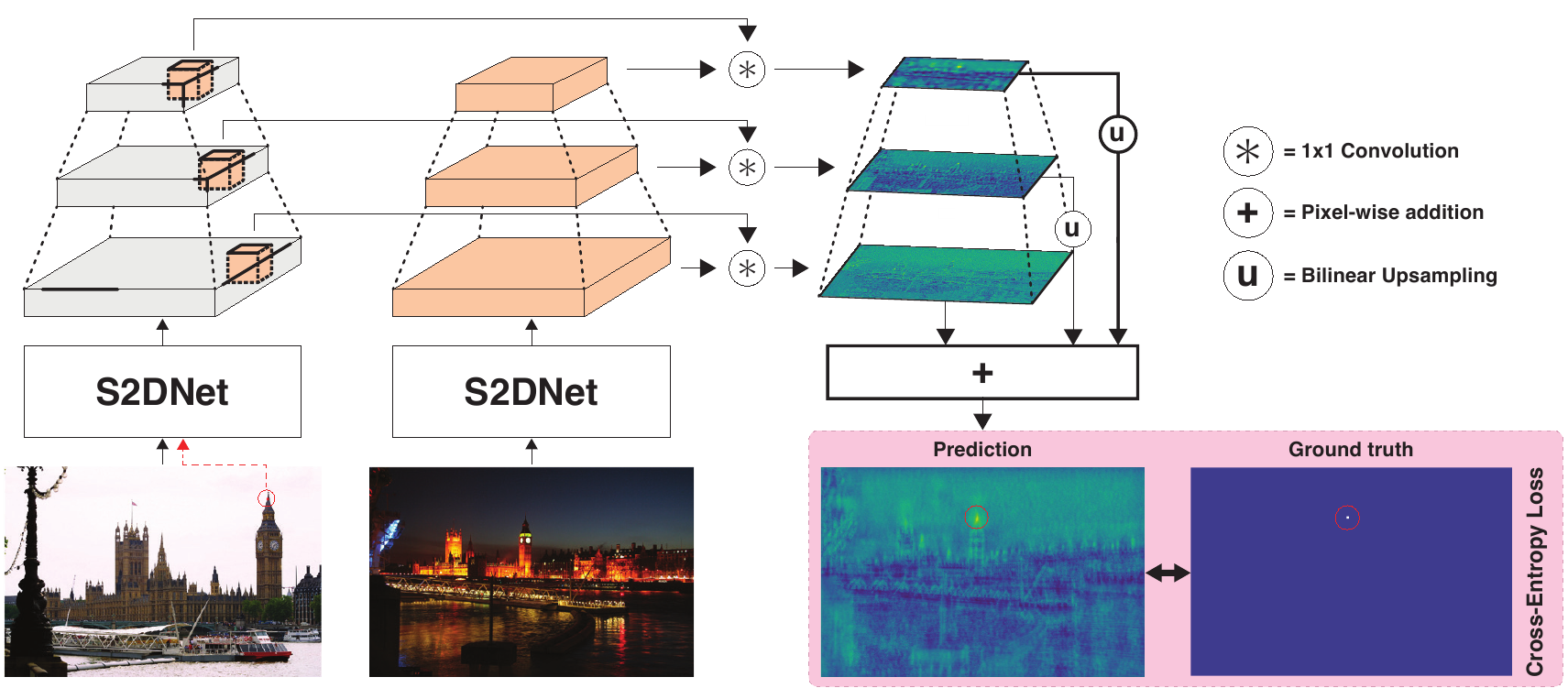
Структурно, авторы берут сеть аналогичную VGG, но при этом забирают не только выход с последнего слоя, но и выходы с более ранних слоёв, чтобы учесть высокочастотные свойства области вокруг точки.

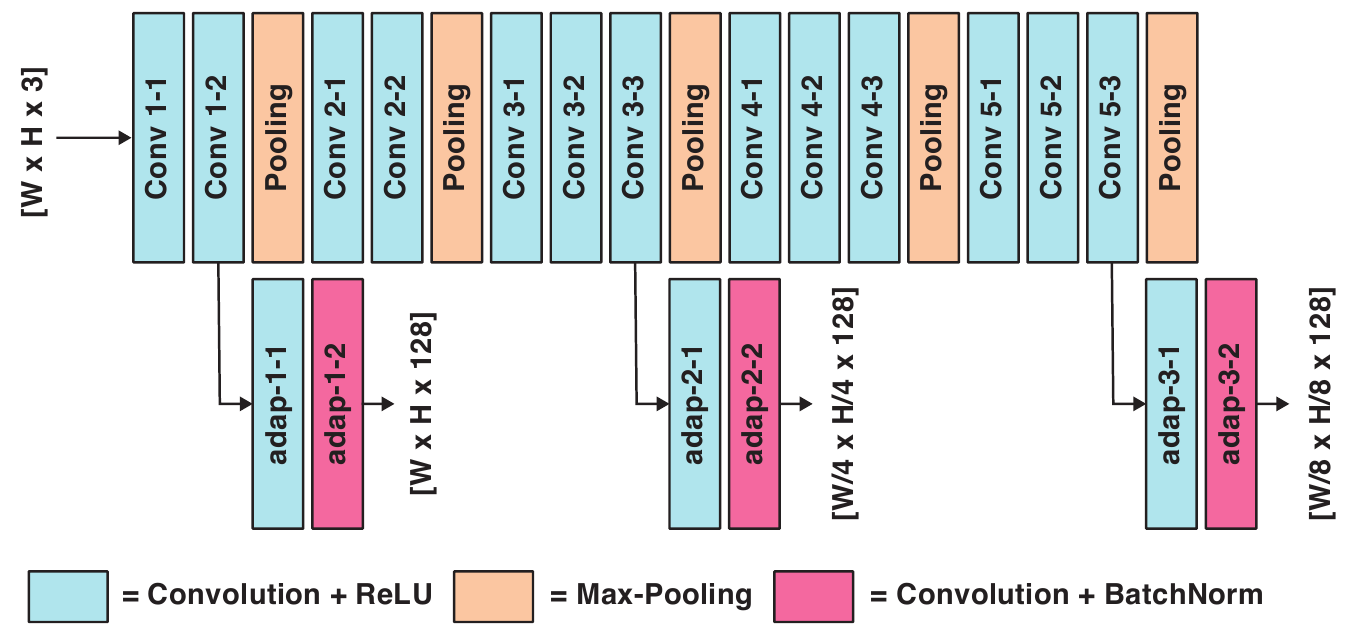
Прогоняя через эту сеть оба изображения, получаем два набора откликов:

\[\left\{ H^m_1 \right\}_{m=1}^M = \mathcal{F}(I_1, \Theta)\]

и

\[\left\{ H^m_2 \right\}_{m=1}^M = \mathcal{F}(I_2, \Theta)\]

Теперь объединим, отклики изображения $I_1$ взятые вокруг точки $p^k_1$ с откликами изображения $I_2$ в карту $C_k$:

\[C_k = \sum_{m=1}^{\infty} \mathcal{U} \left(H^m_1([p^k_1]_m) \ast H^m_2 \right)\]

здесь:

• $[\,\cdot\,]_m$ - масштабирование координат точки изображения на уровень $H^m_1$,

• $\ast$ - оператор свёртки $1 \times 1$,

• $\mathcal{U}$ - оператор билинейного масштабирования тензора в размер изображения $I_2$.

Чтобы натренировать сеть, авторы берут датасет из статьи про D2-Net. Там использовались изображения из Megadepth Dataset на которых авторы D2-Net автоматически разметили парные точки пользуясь знаниями о гомографии, связывающей пары картинок.

Т.к. фактически авторы решают задачу классификации точек изображения на принадлежность классу “таже точка, что и $p_1$ на другом изображении”, то в качестве штрафной функции выбрана кроссэнтропия. При этом ground truth точка не “размывается”, т.е. ищется именно точное соответствие. Потому что, например, D2-Net, как мы выяснили, давала неплохие матчинги, но только если точность опустить ниже 6.5 пикселей.

Когда сеть натренирована, можно использовать её выход $C_k = {\rm S2DNet}(I_1, I_2, p^k_1; \Theta)$ для определения соответствующей точки просто выбрав координаты в которых значение функции $C_k$ максимально:

\[p^k_2 = \arg\max_{p \in I_2} C_k(p)\]

При таком подходе, какая-нибудь точка всегда найдется и, чтобы отсечь совсем неприемлимые варианты, авторы предлагают использовать порог $\tau \in (0,1)$ и оставлять точку только если

\[P(p^k_2 | I_1, I_2, p^k_1, \Theta) > \tau\]

При тестировании авторы выбирают $\tau = 0.2$.

Результаты

В статье есть несколько вариантов тестирования алгоритма, везде получились очень хорошие результаты. Например, авторы использовали тот же протокол, как и в статье про D2-Net. Т.е. из датасета HPatches брали наборы из 6 связанных изображений. 52 набора с изменением освещения, но фиксированной точкой съёмки, и еще 56 наборов с фиксированным освещением, но с изменяющейся точкой съёмки. Для тестов брали первое изображение из набора и матчили из с оставшимися пятью, т.е. получилось $5 \cdot (52+56) = 540$ пар.

Поскольку своего детектора у авторов статьи нет, то они использовали в качестве детектора SuperPoint, а точнее её детектирующую часть. Плюс дополнительно они отбрасывали пары точек, если после перематчивания найденной точки со второго изображения на первое, результат не совпадал с исходной точкой.

Судя по графикам, качество нового подхода существенно выше других:

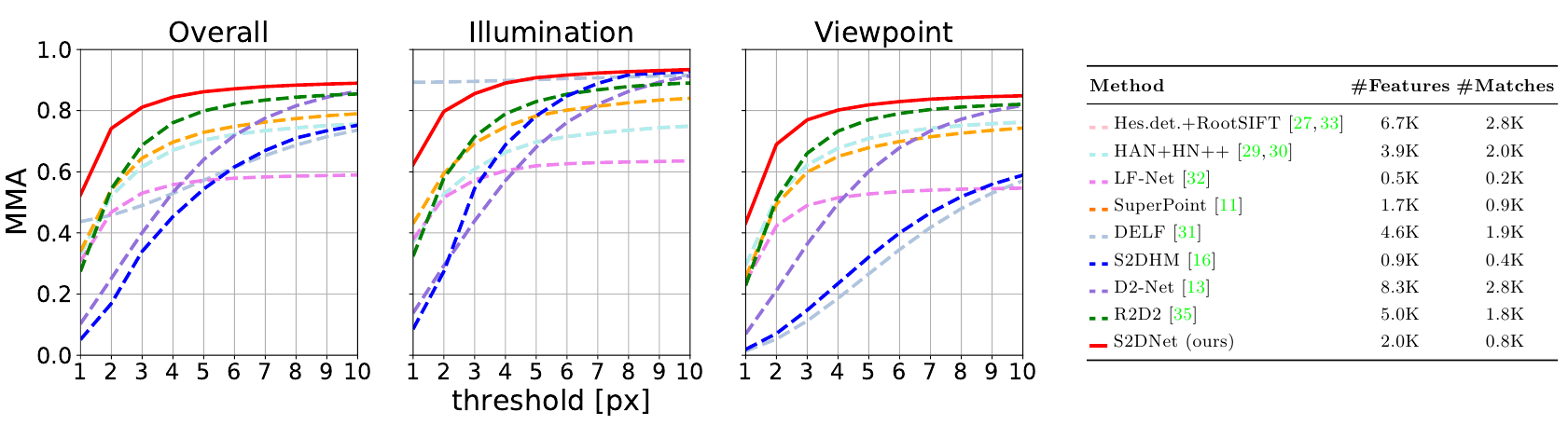
В данном соревновании новый алгоритм уступает только DELF на наборе, где у изображений меняется освещенность, но не меняется точка наблюдения. Это связано с особенностями того как работает DELF и при этом не помогает в среднем.