arXiv:2203.08124

В статье предлагается интересный способ визуализации результатов работы нейронной сети, который позволяет получить представление о границах, разделяющих разные классы (по предсказанию сети). На базе этого способа авторы сравнивают конфигурацию границ классов для сетей различных архитектур, оценивают устойчивость сети одной и той же архитектуры при тренировки с разными начальными весами. Наконец, смотрят как меняется конфигурация областей классов, когда сложность сети меньше, близка и больше интерполяционного порога, что возвращает нас к ситуации двойного спуска

Визуализацию авторы предлагают строить следующим образом. Возьмём три изображения, т.е. три точки в пространстве данных $x_1, x_2, x_3 \in [0, 1]^n$, и построим гиперплоскость на векторах $\vec{v}_1 = x_2 - x_1$ и $\vec{v}_2 = x_3 - x_1$. Если быть более точным, то авторы предлагают брать кусок гиперплоскости:

где $-0.1 \le \alpha, \beta \le 1.1$.

В качестве примера, авторы берут три случайных изображения, по одному из классов Самолет, Лягушка и Птица в датасете CIFAR-10 и строят области классов, определяемых разными сетями:

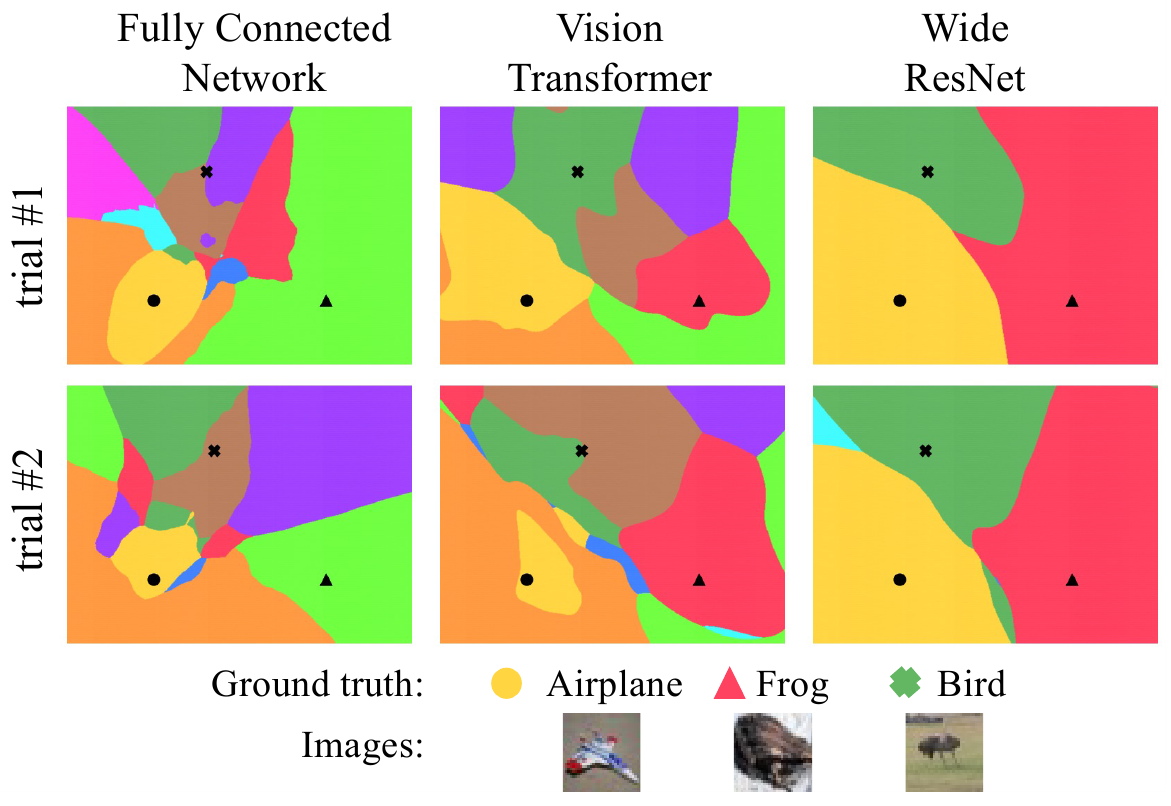
в разных столбцах - сети разных архитектур. В разных строках, две тренировки одной и той же модели, инициализированные разными случайными весами. Разные цвета - разные классы. Уже даже по этому рисунку можно увидить разницу в “гладкости” областей и разной устойчивости разных моделей к изменению начальных весов.

Параметры экспериментов

Эксперименты проводились на CIFAR-10, для тренировки данные расширялись случайным кропом и отражением относительно вертикальной оси. Отметим, что авторы постарались и для экспериментов использовали большое количество разных моделей: FC (полносвязная сеть, 5 скрытых слоёв, ReLU в качестве нелинейности), DenseNet-121, ResNet18, WideResNet-28x10, WideResNet-28x20, WideResNet-28x30, ViT (6 слоёв, 8 голов, размер патча 4), MLPMixer (12 скрытых слоёв, внутренняя размерность 512, размер патча 4)), и VGG19. Тренировали при помощи SGD и Adam подобрав параметр скорости обучения из набора. В часте экспериментов использовался Sharpness-Aware Minimization (SAM) с радиусом 0.01.

Устойчивость модели и индуктивный сдвиг (inductive bias)

Результат сведен в следующее изображение:

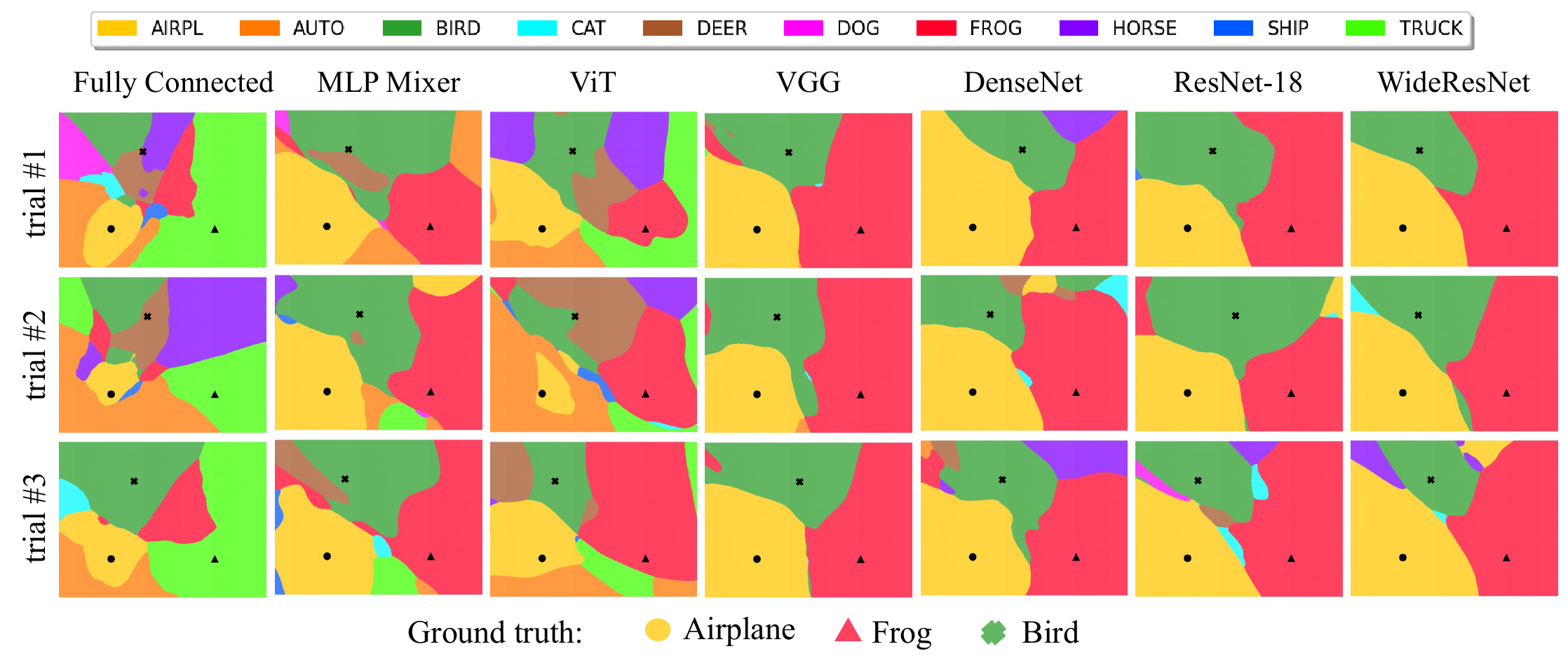
Здесь каждая архитектура (см. столбцы) тренировалась трижды, с разных случайных начальных весов (см. строки).

Авторы отмечают, что все свёрточные модели (DenseNet-121, ResNet18, WideResNet, VGG) генерируют плюс-минус одинаковые регионы классов, а вот регионы полученные от MLPMixer, ViT и полносвязной сети существенно отличаются. Причем у последних трёх области заметно менее гладкие и с существенным вкраплением “посторонних” (т.е. не тех из которых выбранны исходные базисные точки) классов. Например, присутствует большая область соответствующая классу “автомобиль”, которой нет в случае свёрточных сетей.

Так же авторы отмечают, высокую воспроизводимость результатов от тренировки к тренировке, причем эта воспроизводимость существенно выше для свёрточных архитектур. А наиболее сильно проявляется для WideResNet, поэтому авторы предполагают связь между сложностью (шириной) модели и устойчивостью результата по отношению к начальным весам.

Чтобы численно оценить устойчивость архитектуры к разным начальным весам, а так же схожесть архитектур, авторы вводят следующую численную оценку. Допустим есть две натренированные нейронные сети $f(x, \theta_1)$ и $g(x, \theta_2)$ выдающие номер класса по изображению $x$, при этом $f$ и $g$ могут иметь одну и туже архитектуру и отличаться только весами $\theta_1 \neq \theta_2$ полученными в результате тренировки, а могут быть и разных архитектур. Теперь выберем случайным образом тройку изображений $T_i=(x_1, x_2, x_3)_i$ и построим множество точек $S_i$ на гиперплоскости через эти три точки, способом описанным выше. Определим меру схожести моделей $f(\cdot, \theta_1)$ и $g(\cdot, \theta_2)$:

Чтобы оценить $R(f, g)$ для пары моделей, авторы случайным образом выбирают 500 троек изображений, и затем 2500 точек на плоскосте для каждой тройки.

Результат сведен в таблицу (для каждой пары моделей берется 5 разных тренировок, 500 троек, и 2500 точек):

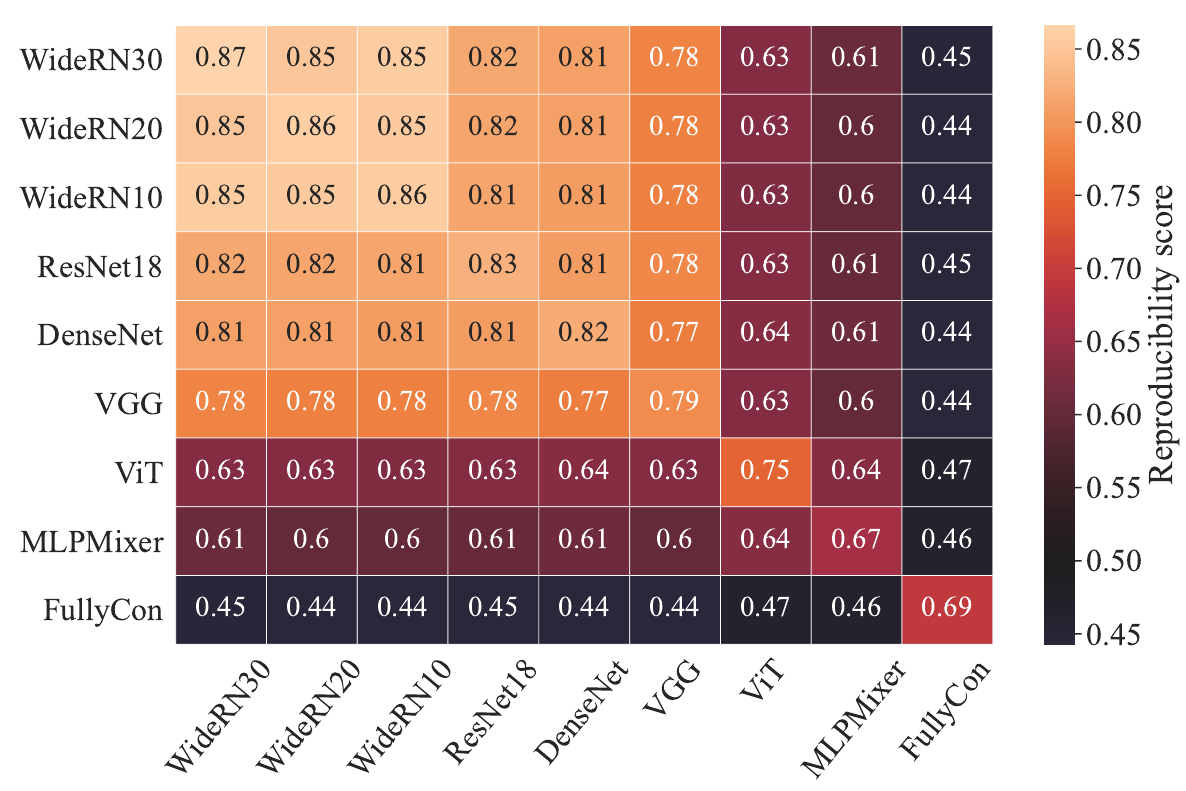
Снова видим, что свёрточные модели очень похожи между собой и отличаются от трех других. Причем MLPMixer, ViT и FC сильно отличаются и от свёрточных сетей и между собой. Воспроизводимость у свёрточных моделей тем выше, чем шире (сложнее) модель, лучшую воспроизводимость 87% показывает самая “широкая” WideResNet-28x30. Однако, авторы отмечают, что ResNet показывает слегка лучшую воспроизводимость, чем очень широкая VGG.

Следующим экспериментом авторы хотят изучить, насколько в процессе передачи знаний, сеть ученик получает похожую на сеть учителя конфигурацию (обычно предполагается, что очень похожую - в том и смысл дистилляции знаний):

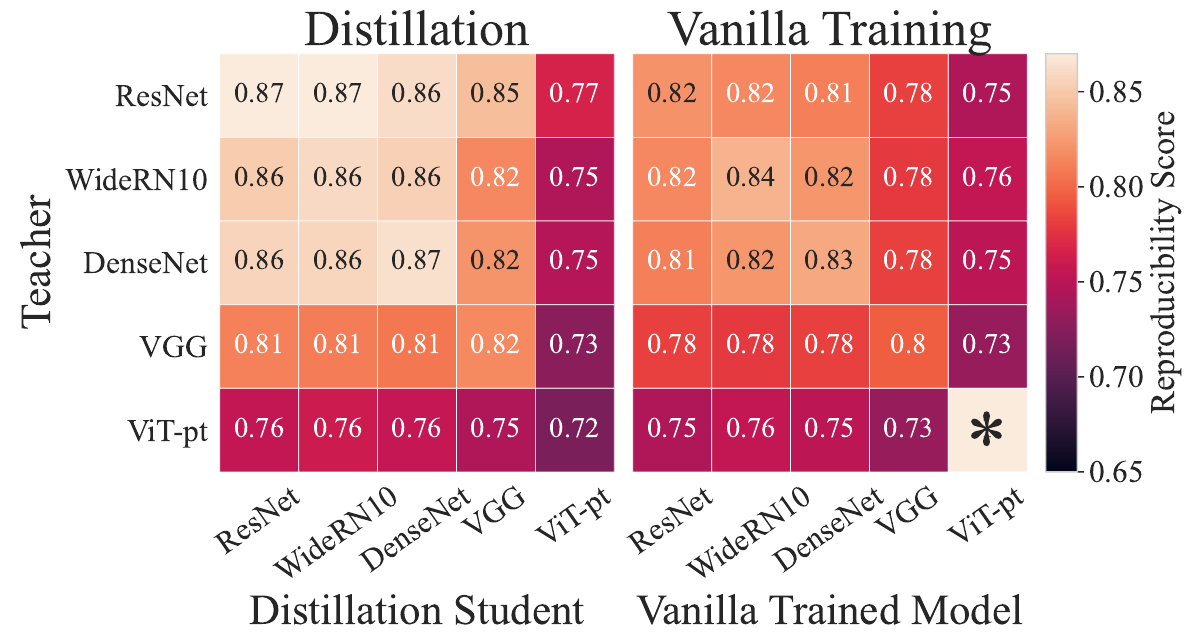
Авторы вычисляют схожесть ученика и его учителя и сравнивают ее со схожестью учителя и сети ученика, но натренированного без передачи знаний, а просто с нуля. Видно, что в случае передачи знания схожесть учителя и ученика существенно выше.

Завершая, авторы сравнивают зависимость воспроизводимости (схожести) сетей одной архитектуры натренированных с использованием разных оптимизаторов:

Сеть        |  Adam   |    SGD  |  SGD+SAM |
----------------------------------- --------
ResNet-18   |  79.81% |  83.74% |   87.22% |
VGG         |  81.19% |  80.92% |   84.21% |
MLPMixer    |  67.80% |  66.51% |   68.06% |
VIT         |  69.55% |  75.13% |   75.19% |
--------------------------------------------

Видно, что использование SAM (Sharpness-Aware Minimization) во всех рассмотренных случаях улучшает воспроизводимость. Однако, авторы так же приводят таблицу точности, полученных моделей и здесь вариант натреннированный с SAM не всегда даёт лучшее качество (см. MLPMixer и ViT):

Сеть        |  Adam   |    SGD  |  SGD+SAM |
----------------------------------- --------
ResNet-18   |  93.04% |  95.30% |   95.68% |
VGG         |  92.87% |  93.13% |   93.90% |
MLPMixer    |  82.22% |  82.04% |   82.18% |
VIT         |  70.89% |  75.49% |   74.72% |
--------------------------------------------

Двойной спуск

Эффект двойного спуска мы уже разбирали. Авторы ставят эксперимент похожий на тот, что был во второй статье: берут датасет CIFAR-10, зашумляя разметку тренировочной части, а именно для каждого изображения оставляя правильную метку с вероятностью $1-p$ или с вероятностью $p$ заменяя ее на случайно выбранную из 10 возможных, для данного датасета. В качестве модели выбрана ResNet18 у которой меняется мультипликатор $k$ количества фильтров свёрточных слоёв $[k, 2k, 4k, 8k]$ и тем самым регулируется сложность модели (классическая ResNet18 получается при $k=64$). Результат точности в зависимости от $k$:

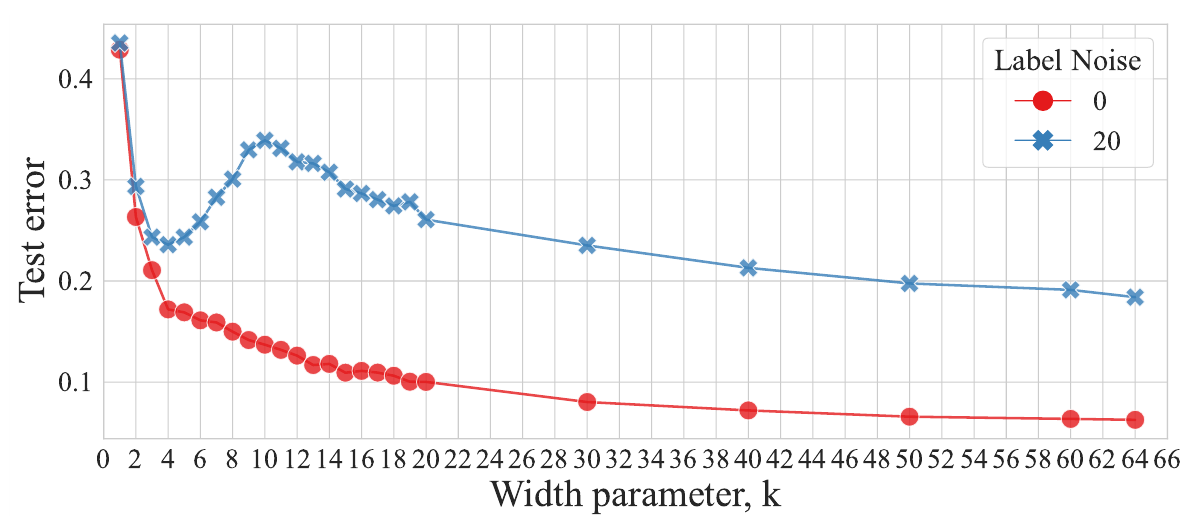
На зашумленных данных при росте сложности модели отчетливо видны пик и второй спад. Из этого графика можно сделать вывод, что лучшая модель (в случае зашумленных на 20% данных) для недопараметризованного режима будет при $k=4$, а интерполяционный порог возникает при $k=10$.

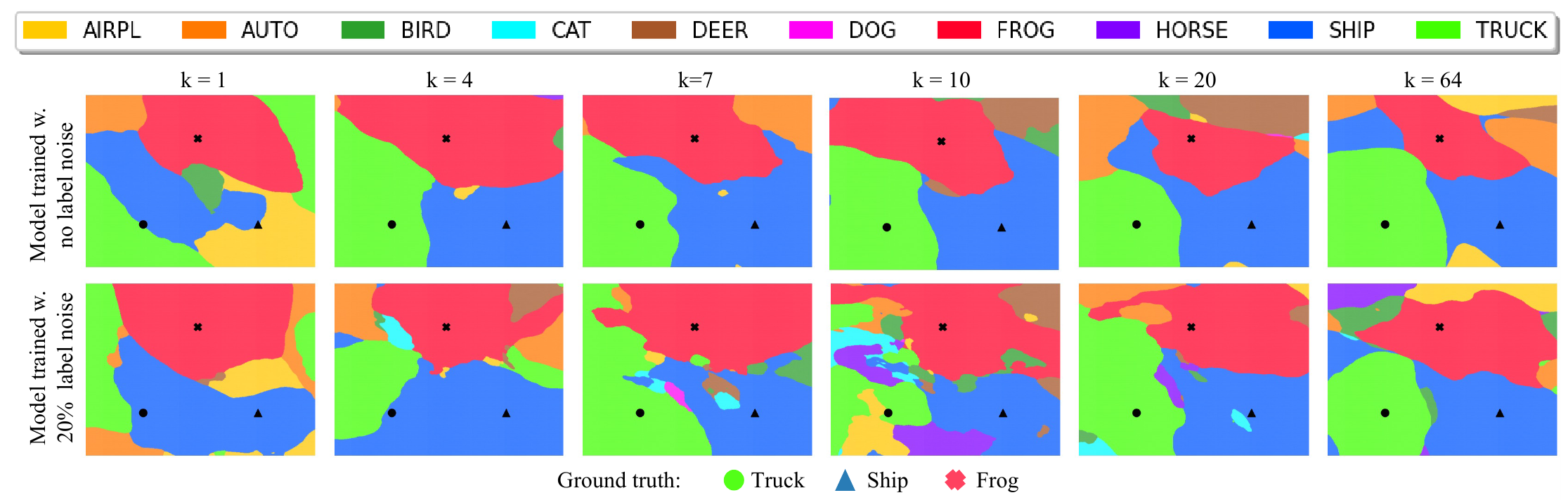
Далее авторы снова применяют свой способ визуализации областей классов и их границ, получается следующая картина для моделей разной сложности на зашумленных и чистых данных:

и еще один вариант, когда точки-изображения на которых строится гиперплоскость берутся из одного класса:

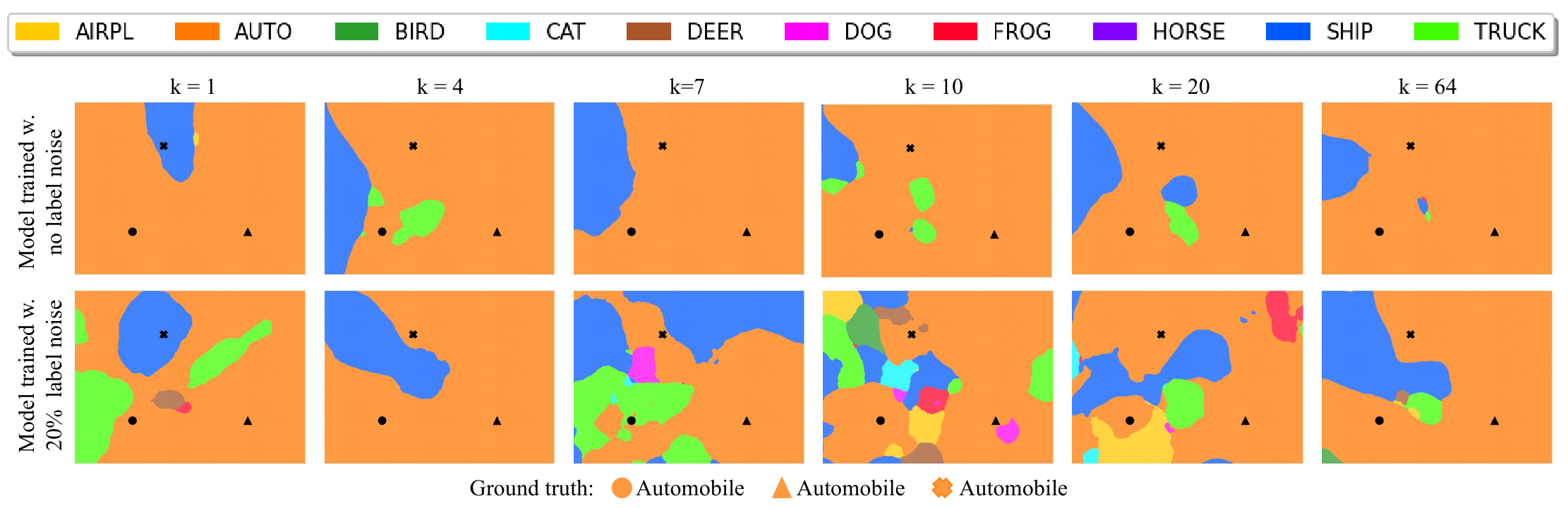
Надо отметить, что точки на которых строится гиперплоскость на картинках выше всегда берутся, имеющие правильные метки (даже в случае зашумленных данных).

Глядя на картинки видно, что для случая “чистых” данных уже начиная с $k=4$ модель генерирует гладкие области и картинка этих областей слабо меняется с ростом сложности модели. На зашумленных данных ситуация кардинально другая, для недопараметризованного режима ($k \le 4$) модель правильно классифицирует не все выбранные точки. Для сложности близкой к интерполяционному порогу ($k=10$) области классов сильно фрагментируются и хаотизируются, появляется много мелких вкраплений областей “неправильных” классов. Наконец, при дальнейшем усложеннии модели фрагментация областей уменьшается, а их границы сглаживаются.

Авторы приводят еще одну картинку для $k=10$, построенную на трех правильно размеченных изображениях из одного класса:

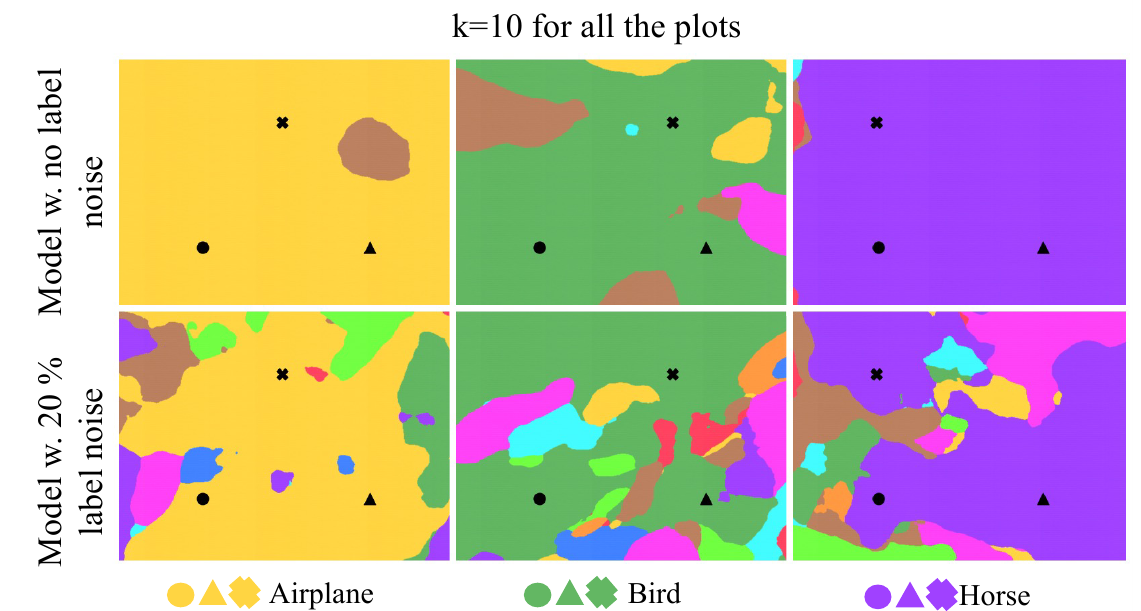
видно, что снова на зашумленных данных области решений сильно фрагментированы и нестабильны, внутри области одного класса появляются мелкие вкрапления областей других классов.

Далее авторы рисуют картину, когда берется три изображения автомобилей, но при этом у одного из них в датасете выставлена неправильная метка:

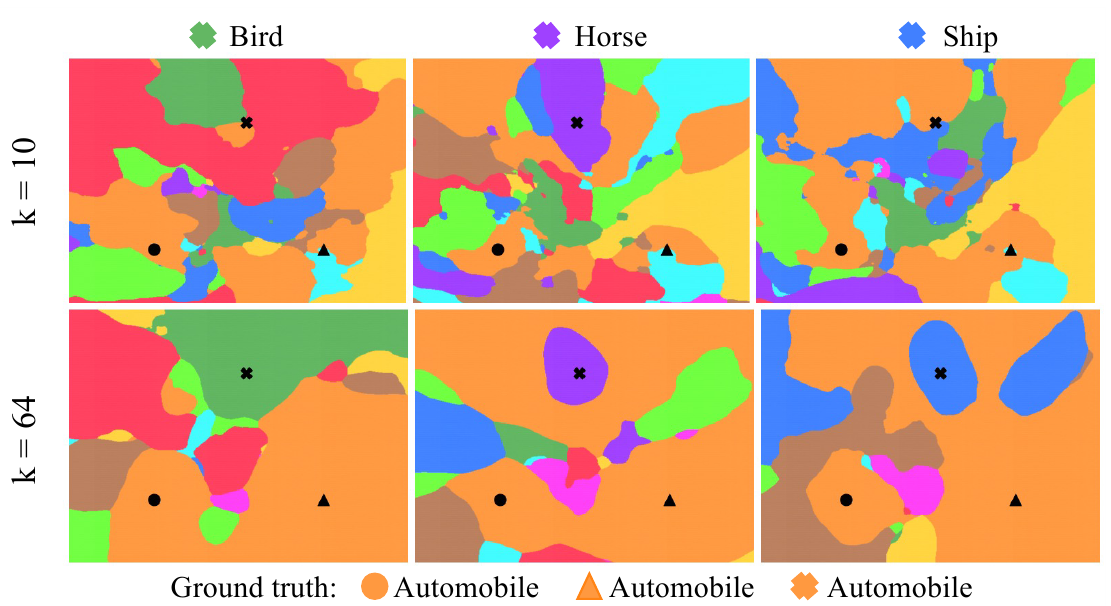
Видно, что при $k=10$ (интерполяционный порог), изображение с неправильной меткой, попадает в класс неправильная метка которого ему присвоена, но лежит ближе к границы области этого класса. Для $k=64$ вокруг этих точек уже формируется “выпуклая” область неправильного класса и граница этой области достаточно гладкая.

Итак качественная оценка ситуации, заключается в том, что область решений у сетей со сложностью близкой к интерполяционному порогу будет “сильно фрагментированной”. Далее авторы предлагают формализовать количественную оценку фрагментированности.

Определим, как делали это выше, по трём точкам $T_i$ множество $S_i$ на гиперплоскости, и взяв сеть $f(\cdot, \theta)$ разложим это множество в объединение $f(S_i, \theta) = \bigsqcup_{j}^{N}P_j(f, \theta)$, где $P_j$ не пересекающиеся, максимальные, связные области точек классифицированных в один класс сетью $f(\cdot, \theta)$, количество таких областей зависит от исходных трех точек $T_i$ и конкретной сети: $N = F(f,\theta, T_i)$. Далее авторы определяют, меру фрагментированности нейронной сети (или просто классификатора) как:

На практике авторы берут 1’000 случайных троек и для каждой считают фрагментацию (используют watershed для выделения связных регионов), а затем усредняют. Теперь авторы строят график зависимости фрагментированности от сложности модели:

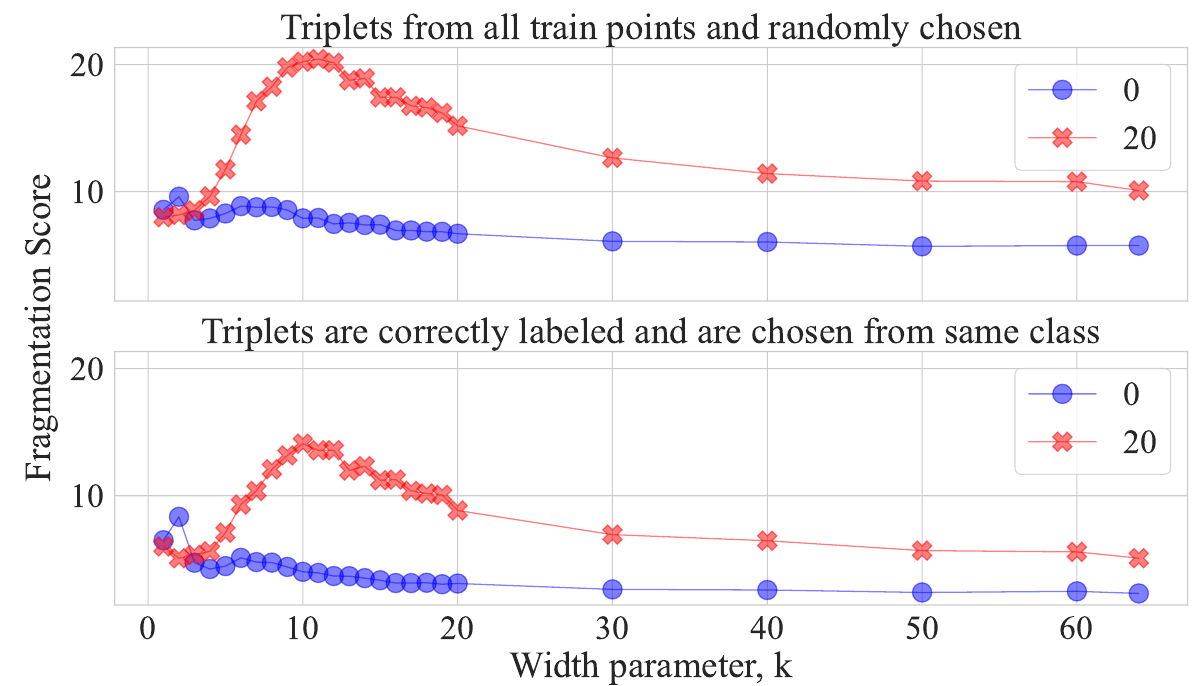
График подтверждает гипотезу, что для моделей со сложностью рядом с интерполяционным порогом, на зашумленных данных наблюдается максимум фрагментированности. Так же авторы отмечают, что для моделей, которые тренировались на данных без зашумления также наблюдается небольшой пик в районе $k=7$.

Следующий график:

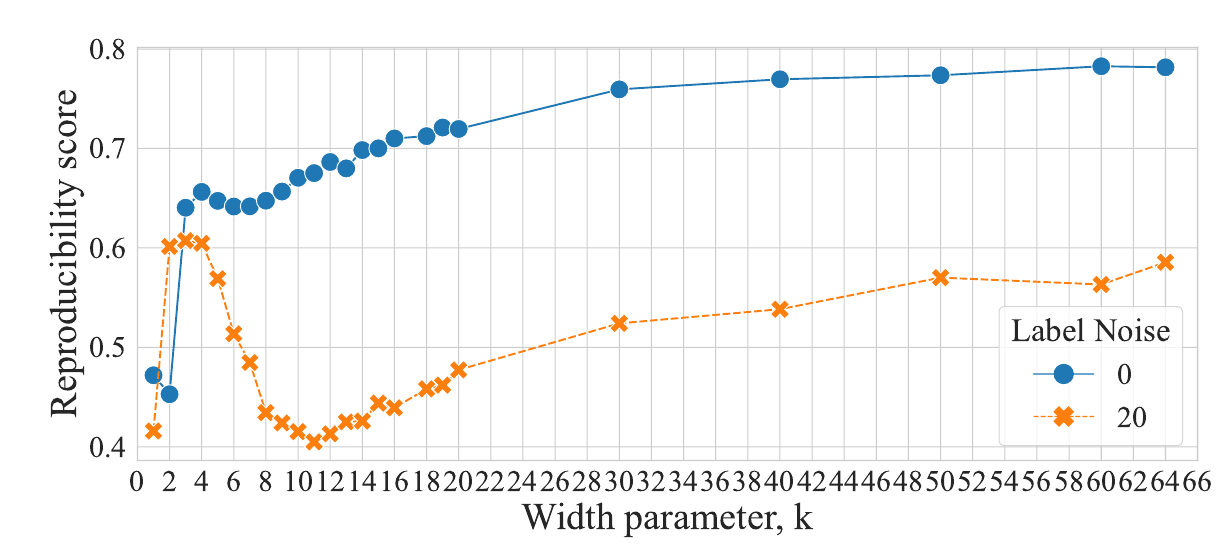
По графику видно, что высокая фрагментированность модели при сложности близкой к интерполяционному порогу, логичным образом влечет малую воспроизводимость. Для зашумленной модели, вокруг $k=10$ происходит существенное падение воспроизводимости, а потом с нарастанием сложности модели, воспроизводимость также растет. Для модели на которой разметка не зашумлялась, проседание воспроизводимости небольшое, но тоже наблюдаемое в районе $k=7$.

И наконец, авторы предлагают разобраться от чего зашумление данных вызывает такой серьёзный эффект причем именно в районе интерполяционного порога. Предлагается два варианта объяснения:

1) возникновение областей “неправильных” классов, которые формируются вокруг изображений, у которых поставили неправильную метку

2) проблемы с границами классов выливающаяся в колебания, которые вредны для интерполяции данных.

Судя по замеченной на графиках выше корелляции, между фрагментированностью и уменьшением точности в районе интерполяционного порога, авторы склоняются к тому, что верен второй вариант. Однако, решают более подробно исследовать и гипотезу 1). Для этого они вводят понятие средний отступ (mean margin) - усредненное расстояние от изображения (как точки) до границы области класса, которой принадлежит это изображение в случайном направлении. Для численной оценки они берут 10 случайных направлений для 5’000 изображений и в качестве среднего отступа для модели берут медианное значение. Результаты сведены в график:

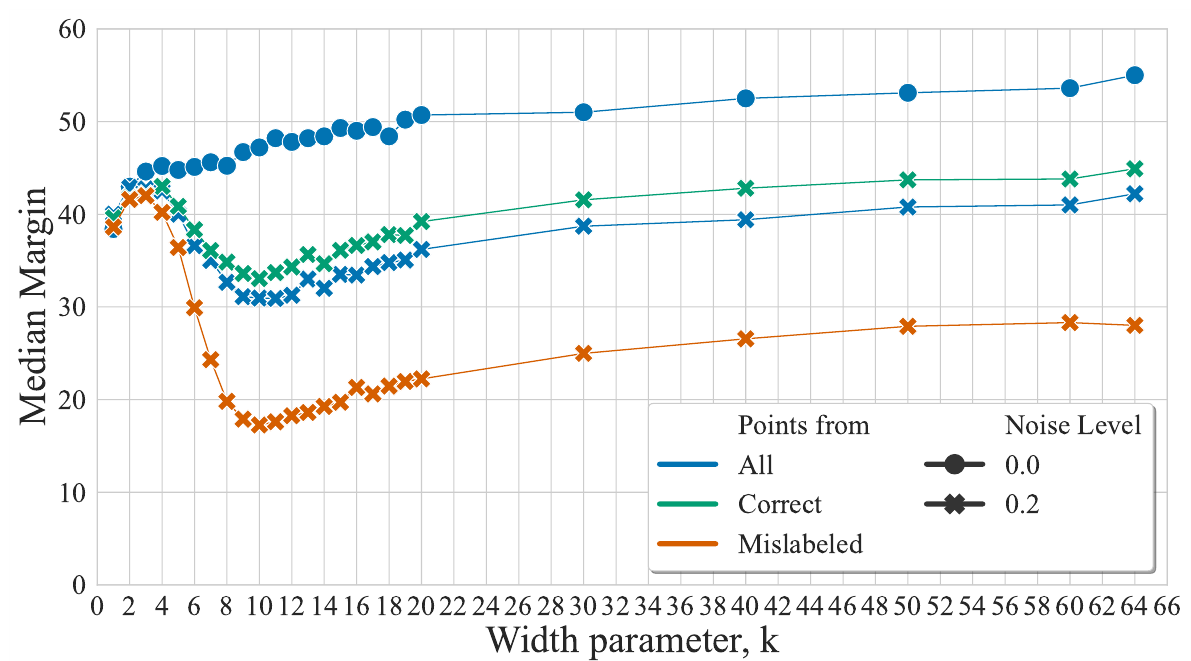
На графике видно, что для $k \ge 10$ с ростом сложности модели растет и расстояние от точки до границы области, но важно то, что это расстояние растёт и для неправильно размеченных изображений, т.е. растет область вокруг неправильно классифицированных изображений, но при этом, как мы знаем, при росте сложности модели происходит второй спуск и ошибка на тестовых данных уменьшается. Т.е. проблема не в росте областей с неправильной классификаций вокруг ошибочно размеченных изображений, а скорее в ненужной осциляции, возникающей из-за нестабильности модели.

Выводы

Статья исключительно познавательная с массой экспериментов и интересных данных.

Авторы отмечают, что неожиданно выясняется, что разные модели нейронных сетей приходят к хорошей точности разными путями. Например, выдающие примерно одинаковые предсказания ResNet-18 и ViT, генерируют существенно различные области классов. Также интересны эксперименты для объяснения эффекта двойного спуска и явно выраженного пика на зашумленных данных, хотя это всё таки, с моей точки зрения, не вполне полное, хотя и весьма интересное обоснование гипотезу о влиянии нестабильностью границ областей решений.