arXiv:2005.13605

Снова про особые точки на изображении. Мы разобрали две статьи sparse-to-sparse подхода: detect-then-describe (SuperPoint ) и detect-and-describe (D2-Net). Также рассмотрели sparse-to-dense подход S2DNet. Сегодня еще одна вариация из разряда sparse-to-sparse - на этот раз с подзаголовком describe-to-detect.

Как очевидно из подзаголовка, авторы предлагают вначале взять сеть, которая хорошо умеет описывать точки изображения, т.е. генерировать для них дескрипторы (в качестве, такой сети в статье предлагаются HardNet или SOSNet), а затем, используя эти дескрипторы, выбрать особые точки.

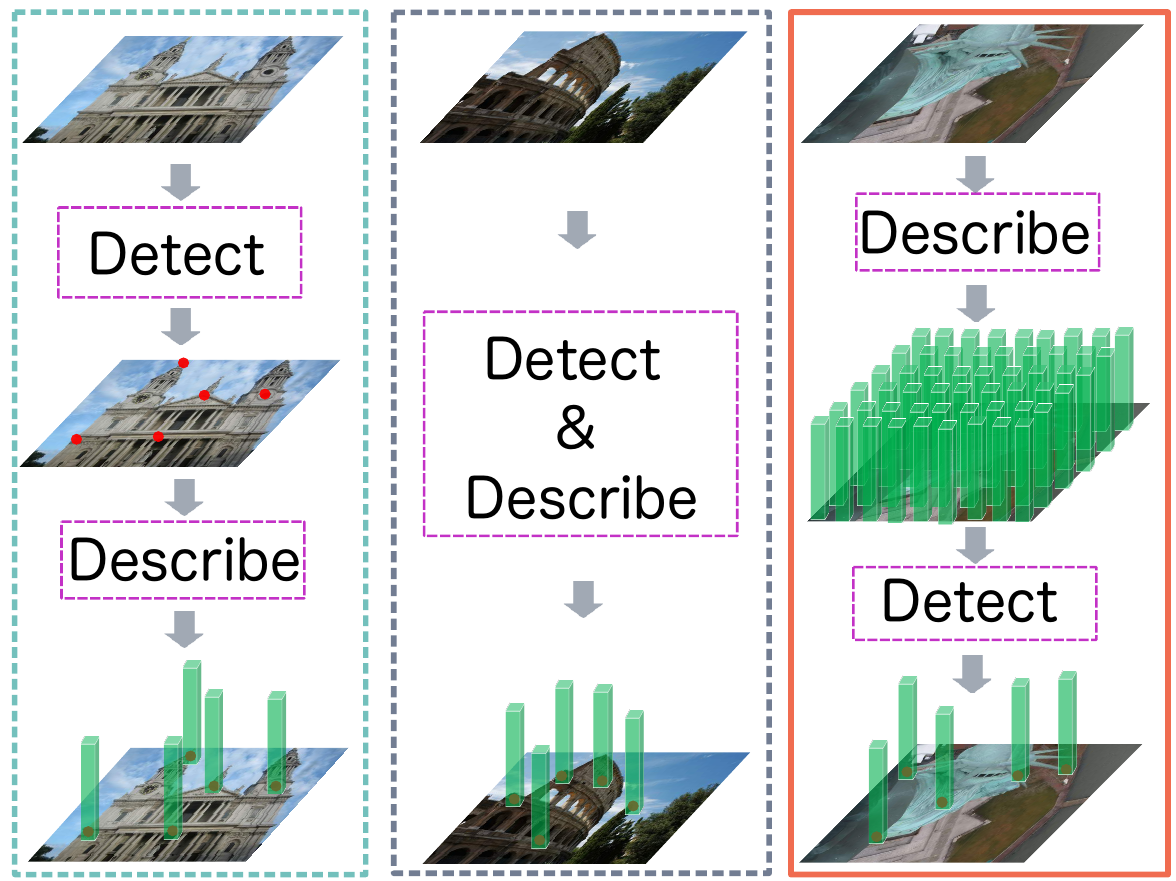
Начинают статью авторы с того, что задают весьма логичный вопрос “А кто же убил Налестро?” “а что такое особая точка?”.

И приходят к заключению, что точку можно считать особой, если ее дескриптор обладает двумя свойствами:

1. Абсолютная особенность - точка (вернее её дескриптор) должна содержать большой объем информации сама по себе. Например, таким свойством обладает центр циферблата или вершина башни.

2. Относительная особенность - дескриптор точки должен отличаться от дескрипторов других точек в локальной окрестности.

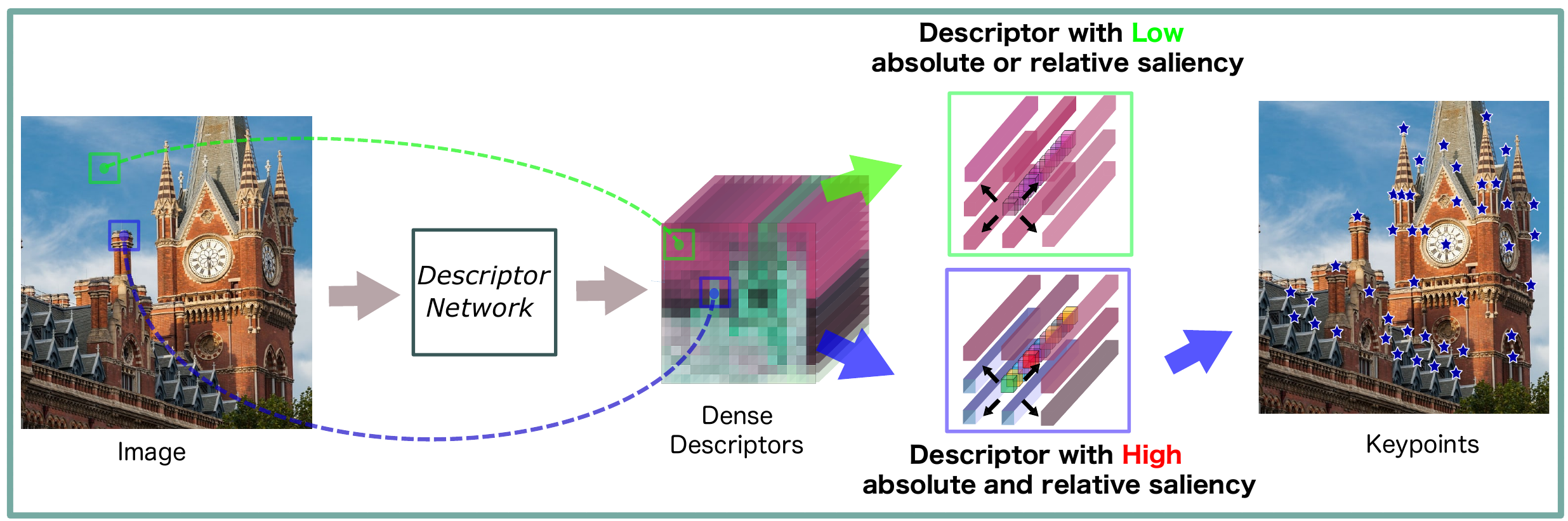
Т.о. дескриптор ключевой точки должен быть, во-первых, информативным, во-вторых, отличимым от других дескрипторов. Осталось формализовать эти требования.

Предположим, у нас есть свёрточная сеть, которая преобразует изображение в тензор дескрипторов. Нам надо определить две численные оценки: абсолютную и относительную особенность дескриптора $F(x,y) \in \mathbb{R}^N$ точки с координатами $(x,y)$.

Поскольку абсолютную особенность ранее определили через объём информации, логично было бы определить меру этой особенности как энтропию дескриптора, но это приведет к сильному усложнению вычислений, поэтому авторы предлагают просто взять в качестве оценки среднеквадратичное отклонение:

\[S_{AB}(x,y) = \sqrt{\mathbb{E}\left(F^2(x, y)\right) - \hat F(x,y)^2}\]

В качестве меры относительной особенности, авторы, аналогично тому как это делается в классических алгоритмах, предлагают использовать взвешенную сумму квадратов разностей. Только если обычно берут разности яркости в исследуемой точке и в точках в её окрестности, то здесь мы будем использовать не яркость, а дескрипторы:

\[S_{RS}(x,y) = \sum_u \sum_v W(u,v) \left \| F(x,y) - F(x+u, y+v) \right \|_2\]

$u$ и $v$ пробегают по окну с центром в $(0, 0)$, для, HardNet и SOSNet в качестве генераторов дескрипторов, авторы выбрали оптимальный размер окна равным $[-5, 5] \times [-5, 5]$.

Наконец общую численную оценку особенности точки, определим в виде произведения абсолютной и относительной оценок:

\[S_{D2D}(x, y) = S_{AB} \cdot S_{RS}(x, y)\]

Результат выглядит примерно следующим образом (в качестве генератора дескрипторов использовалась HardNet):

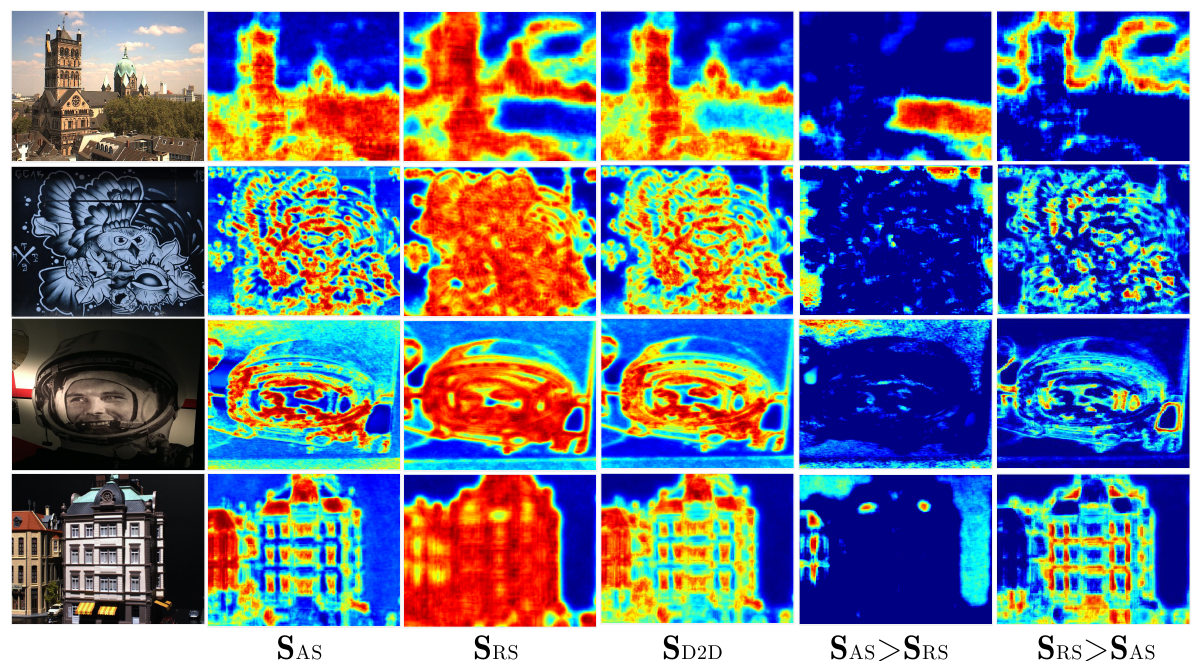
Результаты

В статье есть результаты тестирования с использованием того же протокола, который использовался для D2-Net и S2DNet. Правда S2DNet отсутствует в сравнении скорее всего потому что статьи вышли примерно в одно и тоже время. На самом деле можно примерно сравнить качество S2DNet и текущего алгоритма по представленным графикам.

Итак из датасета HPatches выбираются наборы из 6 связанных изображений. 52 набора с изменением освещения, но фиксированной точкой съёмки, и еще 56 наборов с фиксированным освещением, но с изменяющейся точкой съёмки (подробности как чего оценивали или в статье, или раньше разбирали, когда про D2-Net говорили). Графики результатов:

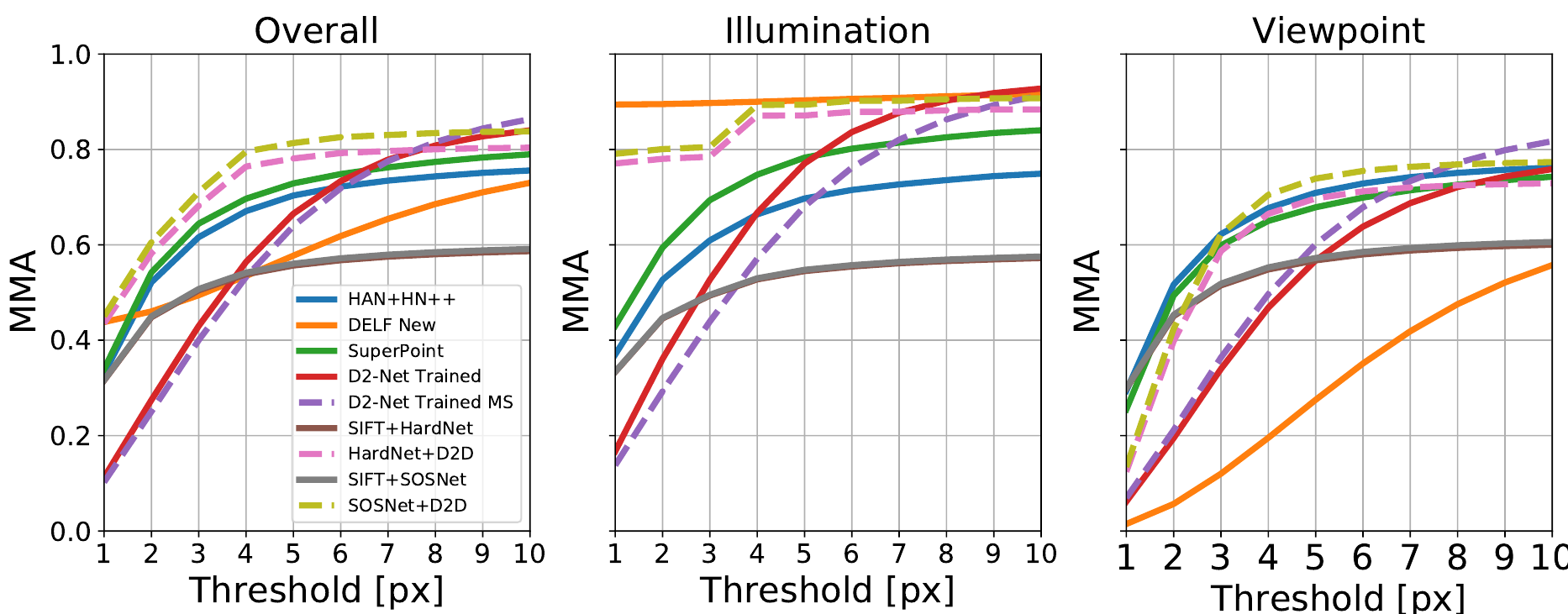
Очевидно, что новый вариант в среднем лучше других. На тестом наборе с изменением освещенности, практически догнал DELF (правда не вполне понятно хорошо ли это), но при изменение точки съёмки начинает перекрывать остальные только на точности около 4 пикселей.

Если вернуться и посмотреть график из S2DNet видно, что S2DNet показывает существенно лучшие результаты (правда чего там со скоростью не очень понятно).