arXiv:1606.09375

Снова про свёрточные сети на графах. Однако в отличии от того, что разбирали в прошлый раз, у нас задача не перекидывать разметку с одних вершин на другие, а, например, классифицировать сигнал на графе. Если сравнивать со свёрточными сетями на изображениях, предыдущую задачу можно было бы сравнить с задачей семантической сегментации, когда часть изображения уже отсегментирована, и на базе этого знания надо доразметить оставшуюся часть. А сегодня мы разберём аналог классической задачи - классификации изображения. Собственно, авторы и проверяют свой подход на классическом датасете MNIST, представив изображения в виде графа и тренируя сетку для классификации. Авторы выложили код, реализующий идеи статьи, что сильно помогает в понимании работы.

Итак у нас снова есть взвешенный неориентированный граф $\mathcal G = (\mathcal V, \mathcal E, W)$, $\mathcal V$ - вершины ($N$ штук), $\mathcal E$ - рёбра и $W \in\mathbb R^{N\times N}$ - матрица весов этого графа. Так же на графе задан некий сигнал $X \in \mathbb R^{N\times C}$, или иначе говоря каждой вершине $i$ приписан вектор особенностей $x^{(i)} \in \mathbb R^C$, необходимо, решить задачу классификации этого сигнала.

Например, авторы берут датасет MNIST и превращают одноканальное изображение размера $28 \times 28$ в одноканальный сигнал на графе ($C=1$). Точки изображения становятся вершинами графа (в количестве $N = 28 \cdot 28 = 784$), рёбра приписываются с использованием алгоритма $8$-ближайших соседей (см. здесь), а веса задаются стандартно для случая, когда вершины имеют координаты в пространстве ($z_i$ - двумерные координаты $i$-ой точки на изображении, нормализованные в отрезок $[0, 1]$):

\[w_{ij} = \exp\left(-\frac {\| z_i - z_j\|^2_2} {\sigma^2}\right)\]

Рёбер кстати получается $\vert\mathcal E\vert = 3’198$ штук, больше чем $(784 \cdot 8) / 2 = 3’136$ потому что берём $8$-ближайших соседей, а не $8$-взаимно ближайших соседей.

Таким образом от задачи классификации изображений (классификации сигнала на двумерной решётке) перешли к задачи классификации сигнала на графе. Хотелось бы иметь возможность использовать подход аналогичный тому, что использовался для изображений, т.е. свёрточную сеть, которая заканчивается полносвязным слоем классификатора.

Как реализовать свёрточные слои при помощи спектрального подхода и полиномов Чебышева мы уже разбирались и даже использовали на практике, хоть и в крайне урезанном виде.

В данной статье, авторы предлагают использовать честный подход с полиномами степени $K \ge 1$ (для MNIST они, например, берут $K = 25$ по аналогии с LeNet-5), тогда $l$-ый свёрточный слой будет выглядеть как:

\[H^{(l+1)}_j = \sigma\left(\sum_{i=1}^{F_l} \left(\sum_{k=0}^{K-1} a^{(l)}_{i,j,k} T_k(\tilde{\mathcal L}) H^{(l)}_i\right) \right),\]

здесь $T_k(\cdot)$ - $k$-ый полином Чебышева, $\tilde{\mathcal L} = 2\mathcal L / \lambda_{max} - I$ - лапласиан графа линейно преобразованный, таким образом, что его собственные числа сдвинулись в отрезок $[-1, 1]$, чтобы можно было использовать полиномы Чебышева,

\[H^{(l)}_i \in \mathbb R^{N},\, i=1,...,F_l\]

отклики $l$-го слоя на графе. И, наконец,

\[a^{(l)}_{i,j,k},\,k=0,...,(K-1),\,i = 1,...,F_l,\,j=1,...,F_{l+1}\]

коэффициенты полинома Чебышева при $k$-ой степени, для $i$-го отклика вершины входного слоя, и $j$ - го отклика той же вершины выходного слоя. $\sigma(\cdot)$ - нелинейность, например, ${\rm ReLU}$.

Загрубление графа и pooling

Pooling для обычной свёрточной сети (обычно max-pooling) это покрытие картинки патчами (обычно квадратными) либо встык, либо с перекрытием, и выбор для каждого патча одного, самого представительного из всех пикселей патча отклика. Обычно при этом геометрический размер карты откликов уменьшается, и можно в каком-то смысле говорить о масштабировании картинки (карты откликов).

Чтобы определить аналогичную операцию, действующую на сигнал на графе, авторы статьи используют загрубление(coarsening) графа. Они предлагают алгоритм сходный с вариантом “паросочетания из тяжелых рёбер”, но с нормализованным весом ребра.

Итак, выбирается случайная непомеченная вершина графа $i$, для этой вершины ищется среди соседних (т.е. соединённых с ней ребром) парная вершина $j$, такая чтобы значение $w_{ij} / (1/d_i + 1/d_j)$ было максимальным. Вершины $i$ и $j$ помечаются, а из их пары получается вершина в загрублённой версии графа. Этот алгоритм во-первых, достаточно быстрый, во-вторых, загрублённый граф содержит приблизительно в два раза меньше вершин чем исходный.

Aвторы предлагают pooling сигнала на графе проделывать, основываясь на этом алгоритме загрублении. Т.е. сигнал в вершине $i$ загрублённого графа, определять как функцию (например, максимум для max-pooling слоя) от сигнала в паре вершин точного графа, которые склеиваются в $i$.

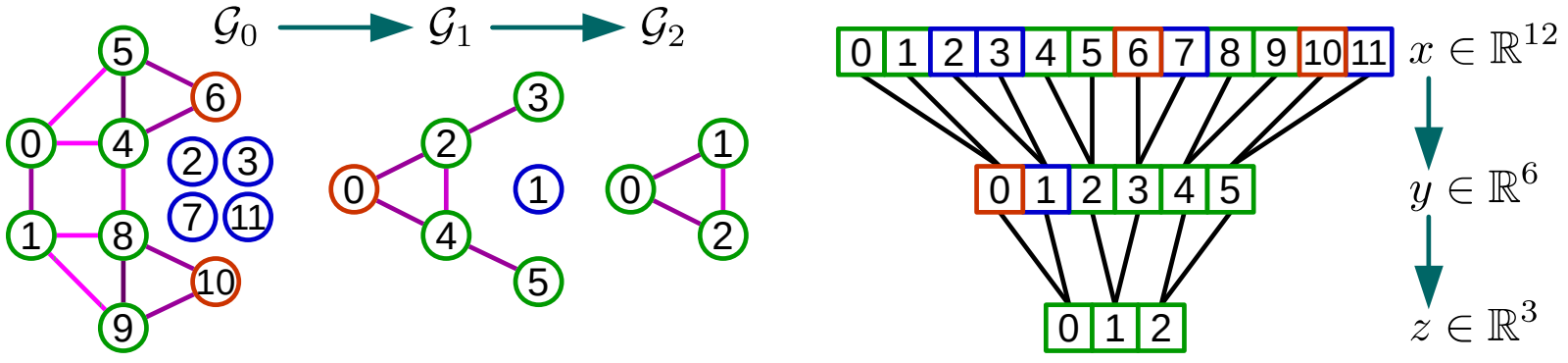
Остаётся одна проблема, чтобы реализовать этот алгоритм, необходимо будет на каждом шаге загрубления запоминать какие вершины в точном графе в какие вершины в загрублённом отображаются. Это несёт существенные накладные расходы. Поэтому авторы предлагают упорядочить вершины таким образом, чтобы процедура pooling-а упростилась до случая одномерного сигнала. Для этого построим сбалансированное бинарное дерево, где на каждом уровне расположены вершины графа соответствующего масштаба, и каждая вершина на уровне $l$ имеет две дочернии вершины на более точном уровне $l-1$. При этом переупорядочим вершины таким образом, чтобы $i$ вершине на шаге $l$ соответствовала пара вершин с индексами $2i$ и $2i+1$ на шаге $l-1$. Теперь применение операции pooling-а становится тривиальной.

Поскольку может так получиться, что при загрублении для каких-то вершин не будет определено пар, авторы вводят фиктивные вершины, с неопределенным значениям сигнала в них. Естественно фиктивные вершины не имеют рёбер.

Возвращаясь к применению графовой свёрточной сети для задачи классификации на MNIST. Авторы пишут что им удалось добиться точности 99.14% для графовой сети типа: GC32-P4-GC64-P4-FC512 (два свёрточных, два pooling, и на выходе полносвязный размерности 512), при этом обычная свёрточная сеть примерно таких же размеров C32-P4-C64-P4-FC512 выдала точность 99.33%. Достаточно малое отставание говорит о том, что, в принципе, графовая сеть в таком виде вполне имеет право на жизнь, и применение её для задач, где графы - естественный вариант (очевидно, что изображение правильнее рассматривать всё-таки как равномерную 2Д решётку, а не граф) должно дать хорошие результаты.