arXiv:1709.04875

Уже разбирали статью про предсказание дорожного трафика, там для решения использовались обычные свёрточные слои и рекуррентные сети (LSTM), но задача в этой статье была относительно простой, за счёт того, что пробки надо было предсказывать на дороге, которая по сути своей представляла некий коридор, т.е. на ней не было перекрёстков и боковых входящих-исходящих дорог. Собственно, поэтому и можно было использовать обычные одномерные свёрточные слои. В данной статье авторы рассматривают более сложные дорожные сети, которые могут быть представлены в виде графов.

В данном случае используются те наработки по свёрточным сетям на графах, с которыми мы сталкивались в статьях: раз и два.

Дорожная сеть может быть представлена в виде графа $\mathcal G = (\mathcal V, \mathcal E, W)$, $\mathcal V$ - вершины ($N$ штук), которые представляют собой точки регистрации дорожного трафика (скорости потока, или количества машин за единицу времени) $\mathcal E$ - рёбра, т.е. дороги соединяющие точки наблюдения и $W \in\mathbb R^{N\times N}$ - матрица весов этого графа (расстояние между точками, например).

У нас есть дискретные временные отсчёты, каждому из которых соответствует вектор $v_t \in \mathbb R^N$ сигнал описывающий значение трафика в точках наблюдения на дорожном графе в момент времени $t$. Задача состоит в предсказании значения этого сигнал в моменты времени $(v_{t+1},…,v_{t+H})$, если известны значения сигнала $(v_{t-M+1},…,v_{t})$.

Архитектура сети

Авторы статьи предлагают использовать пространственно-временную свёрточную сеть на графе (spatio-temporal graph convolutional networks (STGCN)), состояющую из нескольких пространственно-временных свёрточных блоков (spatio-temporal convolutional blocks):

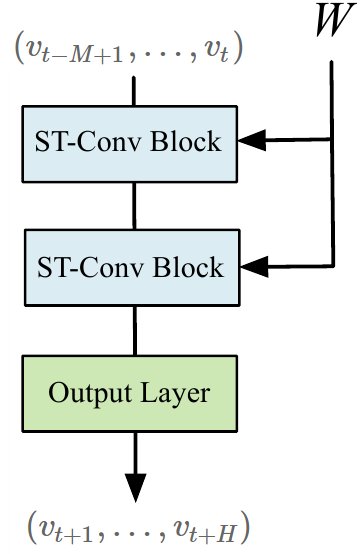
на вход приходится набор сигналов в вершинах графа, соответствующих временным отсчётам в прошлом, пришедшие данные обрабатываются при этом пространственныеми временные зависимости внутри пространственно-временных свёрточных блоков учитываются одновременнно. В результате на выходной слой приходит набор откликов для каждой вершины графа, и затем предсказывается сигнал на графе в временных точках в будущем.

Пространственно-временные свёрточные блоки выглядят как “сэндвич” из двух управляемых свёрточных слоёв (gated sequential convolution layers) со свёрточным слоем на графе (spatial graph convolution layer) между ними:

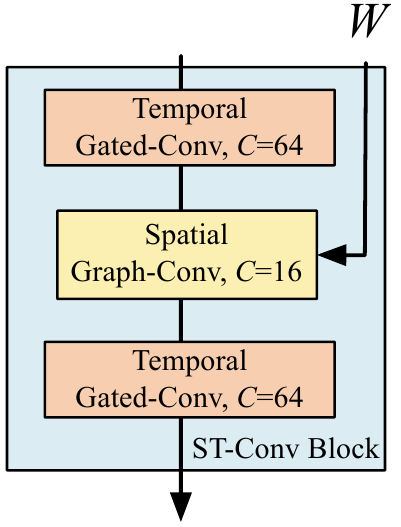
Авторы пробуют два варианта свёрточного слоя на графе, оба мы разбирали ранее, оба используют свёртку $g \ast_{\mathcal G} x$ заданную полиномами Чебышева. Первый вариант оставляет только линейный член полинома Чебышева, и более того использует ренормализованную версию лапласиана $\tilde D^{-1/2} \tilde W \tilde D^{-1/2}$, где $\tilde W = W + I$, а $\tilde D$ - соответствующая диагональная матрица степеней вершин. Такой подход уменьшает количество тренируемых параметров и ускоряет работу сети, а ренормализованный лапласиан добавляет устойчивости вычислениям. При необходимости, можно делать стек из нескольких таких свёрточных слоёв, добиваясь эффекта сходного с использованием полиномов Чебышева степени больше единицы для аппроксимации свёртки.

Второй вариант мы тоже разбирали. В нём честно используются полиномы Чебышева степени выше единицы. И это тоже работает как было показано в соответствующей статье.

Важно отметить, что свёрточный слой с одними и теми же параметрами (коэффициентами полиномов Чебышева) применяется параллельно к $M$ сигналам на одном и том же графе, каждый сигнал соответствует своему временному отсчёту. Авторы статьи выбрали именно такой вариант, но можно было значения в разные моменты времени использовать как $M$-мерный вектор откликов в каждой вершине, и уже в первом слое использовать свёртку с многоканальным входом. Правда это существенно увеличило бы количество тренируемых параметров и потребные вычислительные ресурсы.

Блоки из управляемых свёрточных слоёв обрабатывают временные зависимости данных. Обычно, для обработки временных последовательностей, используются рекуррентные сети, но в данном случае авторы используют GLU блок. Этот блок получая на вход последовательность длины $M$ векторов размерности $C_{in}$ сворачивает её с ядром размера $K_t$ и получает последовательность векторов размерности $2\cdot C_{out}$. Вектора полученной последовательности разбиваются на две равные части, и одна часть используется в качестве “ворот”:

\[Y = \Gamma(X) = \left(X \ast W + b\right) \odot \sigma \left(X \ast V + c\right)\]

В исходной статье про GLU, входная последовательность данных дополнялась $(K_t - 1)$-им фиктивным элементом перед начальным, чтобы после свёртки длина последовательности оставалась неизменной. В данном случае этого не делается, поэтому из входной последовательности $X \in \mathbb R^{M\times C_{in}}$ на выходе получится последовательность короче на $(K_t - 1)$ вектор: $Y\in \mathbb R^{(M - K_t + 1)\times C_{out}}$. Отметим, что такое преобразование применяется к последовательности векторов в каждой из вершин графа. Для первого слоя входная последовательность одноканальная $C_{in} = 1$.

Объединяя наш “сэндвич” получим, что $l$-ый пространственно-временной свёрточный блок представляет из себя функцию вида:

\[v^{(l+1)} = \Gamma^{(l)}_1\left({\rm ReLU}\left( g^{(l)} \ast_{\mathcal G} \Gamma^{(l)}_0(v^{(l)}) \right) \right),\]

на вход которой подаётся тензор $v^{(l)} \in \mathbb R^{M\times N \times C^{(l)}}$, а на выходе получается тензор $v^{(l+1)} \in \mathbb R^{(M - 2(K_t - 1)) \times N \times C^{(l+1)}}$.

Наконец, после двух пространственно-временных свёрточных блоков результат подаётся на выходной слой, который представляет собой обычное линейное преобразование вектора $Z \in \mathbb R^{N \times C}$ в каждой из вершин. Преобразование использует общие для всех вершин веса $A \in \mathbb R^{N \times C}$ и свободный член $d \in \mathbb R$ и считает в каждой вершине значение величины трафика, которую мы хотим предсказать: $\tilde v_{t+1} = A \cdot Z + d$.

В качестве штрафной функции берётся обычный квадрат нормы разности сигналов на графе, предсказанного и ground truth:

\[L = \sum_t \left \| \tilde v_{t+1} - v_{t+1} \right \|^2\]

Авторы проверяют две модели, у обеих в пространственно-временных свёрточных блоках берётся $64$, $16$ и $64$ каналов в трёх слоях. Первая модель (STGCN(Cheb)) использует в свёртке на графе полиномы Чебышева степени $K=3$, вторая (STGCN(1st)) используются вариант с линейной аппроксимацией и ренормализованным лапласианом.

На обоих датасетах (BJER4 и PeMSD7) на которых авторы тестировали свои модели, во-первых, оба варианта показали лучшие результаты, чем алгоритмы предложенные ранее. Во-вторых, качество STGCN(Cheb) было практически по всем метрикам лучше, чем у STGCN(1st).